Graph Of X 1 X
candidatos
Sep 14, 2025 · 6 min read
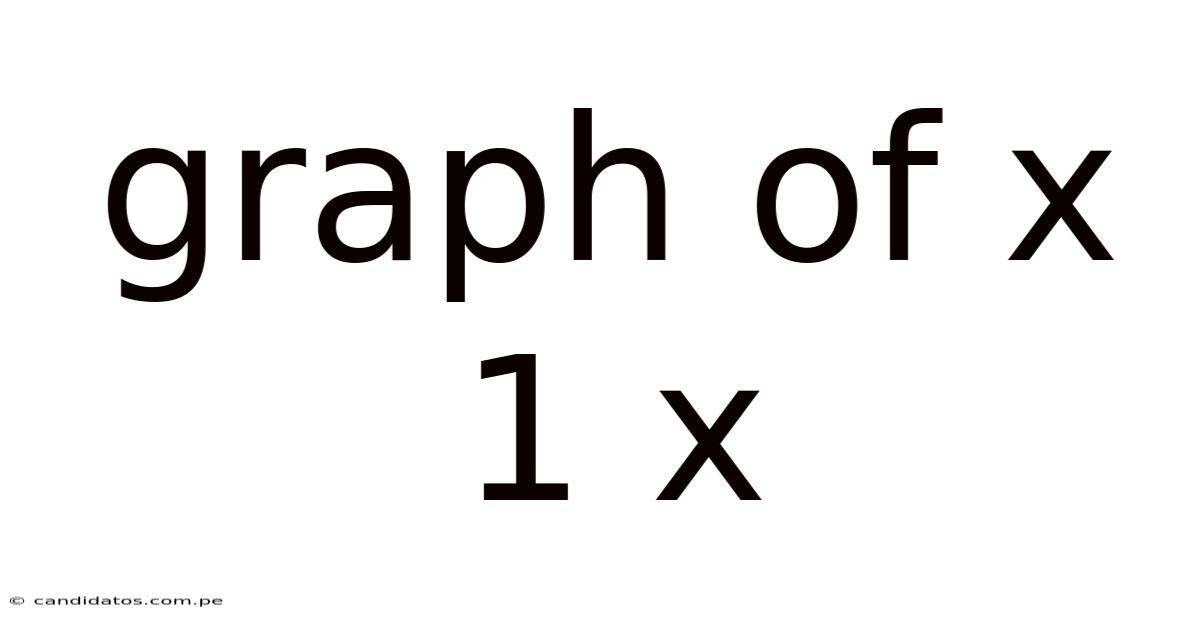
Table of Contents
Unveiling the Secrets of the Graph of x/(x-1): A Comprehensive Exploration
The function f(x) = x/(x-1) presents a fascinating case study in graphical analysis. Understanding its behavior requires a blend of algebraic manipulation, calculus techniques, and insightful interpretation. This article will delve deep into the characteristics of this function, exploring its domain, range, asymptotes, intercepts, and overall shape, equipping you with a thorough understanding of its graphical representation. We'll also address common misconceptions and frequently asked questions.
Introduction: Setting the Stage
The graph of x/(x-1) is a rational function, meaning it's a ratio of two polynomial functions. Rational functions often exhibit interesting behavior, including asymptotes (lines the graph approaches but never touches) and discontinuities (points where the function is undefined). These features are key to understanding its visual representation. This exploration will go beyond simply plotting points; we'll unravel the underlying mathematical principles governing its shape and behavior. We will examine its key features, including its vertical and horizontal asymptotes, x and y intercepts, and its behavior as x approaches positive and negative infinity. Understanding these aspects will allow you to accurately sketch the graph without relying solely on technology.
1. Determining the Domain and Range:
The domain of a function represents all possible input values (x-values) for which the function is defined. In the case of f(x) = x/(x-1), the function is undefined when the denominator is zero, i.e., when x - 1 = 0, which means x = 1. Therefore, the domain of f(x) is all real numbers except x = 1. We can express this as: Domain: (-∞, 1) U (1, ∞).
The range of a function represents all possible output values (y-values). To find the range, we can analyze the function's behavior. Notice that as x approaches 1 from the left (x → 1⁻), f(x) approaches negative infinity. As x approaches 1 from the right (x → 1⁺), f(x) approaches positive infinity. Furthermore, as x approaches positive or negative infinity, f(x) approaches 1. Therefore, the range of f(x) is all real numbers except y = 1. We can express this as: Range: (-∞, 1) U (1, ∞).
2. Identifying Asymptotes:
Asymptotes are crucial in understanding the behavior of rational functions. There are two main types: vertical and horizontal asymptotes.
-
Vertical Asymptote: A vertical asymptote occurs at values of x where the denominator of the function is zero and the numerator is non-zero. In our case, this occurs at x = 1. As x approaches 1, the function approaches either positive or negative infinity, depending on whether x approaches 1 from the left or the right. Thus, x = 1 is a vertical asymptote.
-
Horizontal Asymptote: A horizontal asymptote describes the behavior of the function as x approaches positive or negative infinity. To find the horizontal asymptote, we examine the degrees of the numerator and denominator polynomials. Since both the numerator and denominator have degree 1, the horizontal asymptote is the ratio of the leading coefficients, which is 1/1 = 1. Therefore, y = 1 is a horizontal asymptote.
3. Finding Intercepts:
-
x-intercept: The x-intercept is the point where the graph crosses the x-axis (where y = 0). To find it, we set f(x) = 0 and solve for x:
0 = x/(x-1) This equation is true only when the numerator is zero and the denominator is non-zero. Thus, x = 0. Therefore, the x-intercept is (0, 0).
-
y-intercept: The y-intercept is the point where the graph crosses the y-axis (where x = 0). To find it, we evaluate f(0):
f(0) = 0/(0-1) = 0 Therefore, the y-intercept is (0, 0).
4. Analyzing the First Derivative (Analyzing Increasing and Decreasing Intervals):
To determine where the function is increasing or decreasing, we need to find the first derivative and analyze its sign. Using the quotient rule:
f'(x) = [(x-1)(1) - x(1)] / (x-1)² = -1/(x-1)²
Since (x-1)² is always positive (except at x=1 where it's undefined), f'(x) is always negative except at x=1. This means that the function is decreasing on its entire domain (-∞, 1) U (1, ∞). There are no local maxima or minima.
5. Analyzing the Second Derivative (Analyzing Concavity):
To determine the concavity of the function, we find the second derivative:
f''(x) = d/dx [-1/(x-1)²] = 2/(x-1)³
The second derivative is positive when x > 1 and negative when x < 1. This tells us that the function is concave up on (1, ∞) and concave down on (-∞, 1). There is no inflection point because the function is undefined at x=1.
6. Sketching the Graph:
Now, armed with all this information, we can accurately sketch the graph:
- Draw the vertical asymptote at x = 1.
- Draw the horizontal asymptote at y = 1.
- Plot the x-intercept and y-intercept at (0, 0).
- Since the function is always decreasing, sketch the curve approaching the asymptotes. Remember the concavity: concave down to the left of x=1 and concave up to the right.
The graph should show two separate branches: one in the region x < 1 and another in the region x > 1, both approaching the asymptotes but never touching them.
7. Common Misconceptions:
-
Thinking the graph crosses the asymptotes: A common mistake is to believe the graph will eventually cross the asymptotes. Asymptotes represent a limit; the graph approaches them infinitely closely but never actually touches them.
-
Incorrectly determining the range: Failing to recognize the horizontal asymptote can lead to an incorrect range. The range is limited by the horizontal asymptote.
-
Forgetting to consider the vertical asymptote's impact on the domain: The vertical asymptote dictates a restriction on the domain of the function.
8. Frequently Asked Questions (FAQs):
-
Q: What happens to the function as x approaches infinity? A: As x approaches positive or negative infinity, the function approaches its horizontal asymptote, y = 1.
-
Q: Is this function continuous? A: No, it's discontinuous at x = 1 due to the vertical asymptote.
-
Q: Does the function have any oblique asymptotes? A: No, oblique asymptotes occur when the degree of the numerator is exactly one greater than the degree of the denominator. In this case, both have degree 1.
-
Q: How can I use this graph to solve inequalities involving x/(x-1)? A: By examining the graph, you can determine the intervals where the function is positive or negative, which can be used to solve inequalities.
9. Conclusion: A Deeper Understanding
The graph of x/(x-1) is more than just a collection of points; it's a visual representation of a function's behavior governed by precise mathematical principles. By systematically analyzing its domain, range, asymptotes, intercepts, and derivatives, we've gained a comprehensive understanding of its characteristics. This detailed exploration demonstrates the power of combining algebraic manipulation, calculus, and graphical interpretation to unlock the secrets hidden within seemingly simple functions. This analysis not only provides a precise sketch but also cultivates a deeper appreciation for the interplay between mathematical concepts and their visual representations. The process of understanding this function serves as a valuable template for analyzing other rational functions and further enhances mathematical intuition.
Latest Posts
Latest Posts
-
Marriage Legal Age In India
Sep 14, 2025
-
50 Lbs How Many Kg
Sep 14, 2025
-
Factorisation Of A Cubic Polynomial
Sep 14, 2025
-
Words That Begin With My
Sep 14, 2025
-
Name A Type Of Metal
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Graph Of X 1 X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.