9 Out Of 12 Percentage
candidatos
Sep 21, 2025 · 6 min read
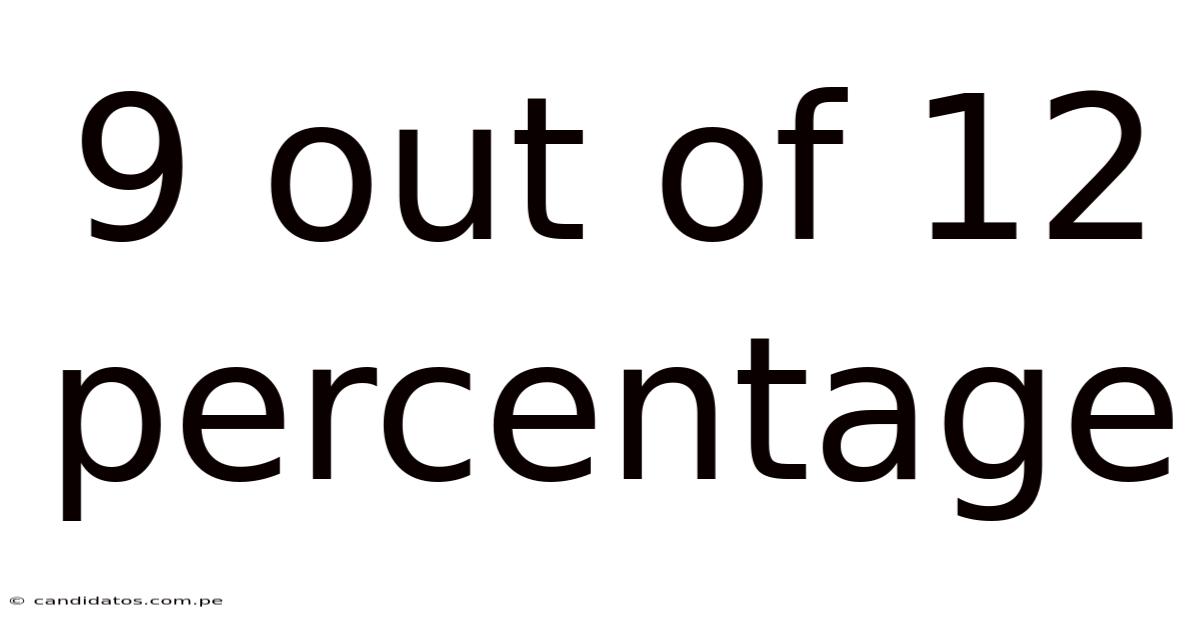
Table of Contents
Decoding the 9 out of 12 Percentage: Understanding Fractions, Decimals, and Percentages
Understanding percentages is a fundamental skill applicable across numerous areas of life, from academic assessments to financial calculations and everyday decision-making. This article delves deep into the seemingly simple concept of "9 out of 12," explaining how to calculate the percentage, its real-world applications, and addressing common misconceptions. We'll explore the underlying mathematical principles, providing a comprehensive guide suitable for learners of all levels.
Introduction: What Does 9 out of 12 Mean?
The phrase "9 out of 12" represents a fraction, specifically 9/12. This fraction indicates that out of a total of 12 items, 9 possess a specific characteristic or meet a particular criterion. To understand its significance, we need to convert this fraction into a more easily interpretable format – a percentage. Percentages express portions of a whole as a number out of 100, making them a standardized way to compare and analyze proportions. This article will provide a step-by-step guide to calculating this percentage and explore the broader context of its meaning. We'll cover various methods, ensuring you grasp the underlying concepts and not just the final answer.
Calculating the Percentage: Step-by-Step Guide
There are several ways to calculate the percentage represented by 9 out of 12. Let's explore the most common methods:
Method 1: Using the Fraction-to-Percentage Conversion
-
Express the fraction: We start with the given fraction, 9/12.
-
Simplify the fraction (optional but recommended): Simplifying the fraction makes the calculation easier. Both 9 and 12 are divisible by 3, resulting in the simplified fraction 3/4.
-
Convert to decimal: To convert the fraction to a decimal, divide the numerator (top number) by the denominator (bottom number): 3 ÷ 4 = 0.75
-
Convert to percentage: Multiply the decimal by 100: 0.75 x 100 = 75%
Therefore, 9 out of 12 is equal to 75%.
Method 2: Direct Percentage Calculation
-
Set up the proportion: We can set up a proportion to solve for the percentage directly: 9/12 = x/100, where 'x' represents the percentage we want to find.
-
Cross-multiply: Cross-multiplying gives us: 12x = 900
-
Solve for x: Dividing both sides by 12 gives us: x = 75
Therefore, 9 out of 12 is equal to 75%.
Method 3: Using a Calculator
Most calculators have a percentage function. Simply enter 9 ÷ 12 and then multiply the result by 100 to obtain the percentage.
Understanding the Result: What 75% Means in Context
The 75% result signifies that 9 represents three-quarters (¾) of the total of 12. This percentage can be interpreted in various contexts, depending on the situation. For instance:
-
Academic Performance: If a student answered 9 out of 12 questions correctly on a test, their score would be 75%.
-
Project Completion: If a project had 12 tasks, and 9 are completed, 75% of the project is finished.
-
Sales Targets: If a salesperson had a target of 12 sales and achieved 9, they reached 75% of their goal.
The interpretation of 75% depends entirely on the context in which the 9 out of 12 scenario arises.
Real-World Applications of Percentage Calculations
Percentage calculations are incredibly versatile and are used extensively across various fields:
-
Finance: Calculating interest rates, discounts, profit margins, tax rates, and investment returns all involve percentage calculations.
-
Statistics: Percentages are vital in summarizing and interpreting data, representing proportions within a sample or population.
-
Science: Many scientific measurements and calculations involve percentages, such as expressing concentrations of solutions or analyzing experimental results.
-
Business: Analyzing sales figures, market share, and customer satisfaction often utilizes percentages.
-
Everyday Life: Understanding percentages helps with calculating tips, discounts in stores, and interpreting statistics presented in news reports.
Common Misconceptions about Percentages
Several common misunderstandings surround percentage calculations:
-
Confusing percentages with absolute values: A 75% increase on a small number is much less significant than a 75% increase on a large number. It's crucial to consider both the percentage change and the absolute values involved.
-
Incorrectly adding percentages: Adding percentages directly without considering the base value can lead to inaccurate results. For example, a 10% increase followed by a 10% decrease does not result in the original value.
-
Misinterpreting percentages over 100%: Percentages exceeding 100% simply indicate a value greater than the base value. This is often seen in contexts such as growth rates.
Advanced Concepts Related to Percentages
Beyond the basic calculation of 9 out of 12, several related concepts expand on the understanding of percentages:
-
Percentage change: This describes the relative change between two values, expressed as a percentage. It's calculated by finding the difference between the two values, dividing by the original value, and multiplying by 100.
-
Percentage points: This term is often misused. It represents the absolute difference between two percentages. For example, a change from 50% to 55% is a 5 percentage point increase, not a 10% increase.
-
Compounding percentages: This involves applying a percentage change repeatedly over time. It's essential in scenarios like compound interest calculations.
-
Weighted averages: When different values have different weights or importance, weighted averages using percentages are calculated to accurately represent the overall value.
Frequently Asked Questions (FAQ)
Q1: How do I calculate a percentage increase or decrease?
A1: To calculate a percentage increase, subtract the original value from the new value, divide the result by the original value, and multiply by 100. For a percentage decrease, the process is similar, but the result might be negative.
Q2: What if I have a fraction with a larger numerator than the denominator?
A2: This results in a percentage greater than 100%, indicating a value larger than the whole. The calculation remains the same; divide the numerator by the denominator and multiply by 100.
Q3: How do I convert a percentage back to a fraction?
A3: Divide the percentage by 100 and simplify the resulting fraction. For example, 75% becomes 75/100, which simplifies to 3/4.
Q4: Are there any online calculators to help me with percentage calculations?
A4: Yes, many websites offer free online percentage calculators that can perform various percentage-related calculations, including those involving increases, decreases, and conversions between fractions, decimals, and percentages. These tools can be especially helpful for complex calculations.
Conclusion: Mastering Percentages for Everyday Success
Understanding percentages is a vital skill with far-reaching applications. This article provided a detailed explanation of how to calculate the percentage represented by 9 out of 12, clarifying the underlying mathematical principles and demonstrating its relevance across numerous contexts. By mastering percentage calculations and understanding related concepts, you equip yourself with a powerful tool for interpreting data, making informed decisions, and succeeding in various aspects of life, from academic pursuits to professional endeavors and beyond. Remember that the key lies not just in obtaining the answer (75%) but in grasping the underlying principles and applying them effectively in different scenarios. The ability to translate fractions, decimals, and percentages seamlessly is a crucial component of numeracy that extends far beyond the classroom.
Latest Posts
Latest Posts
-
Convert 0 45 Into A Fraction
Sep 21, 2025
-
Diagram Of A Flower Labeled
Sep 21, 2025
-
Operation True Love Ch 100
Sep 21, 2025
-
How Do You Spell Questioned
Sep 21, 2025
-
10 Percent Of 1 Million
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 9 Out Of 12 Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.