9 4 Divided By 2
candidatos
Sep 15, 2025 · 6 min read
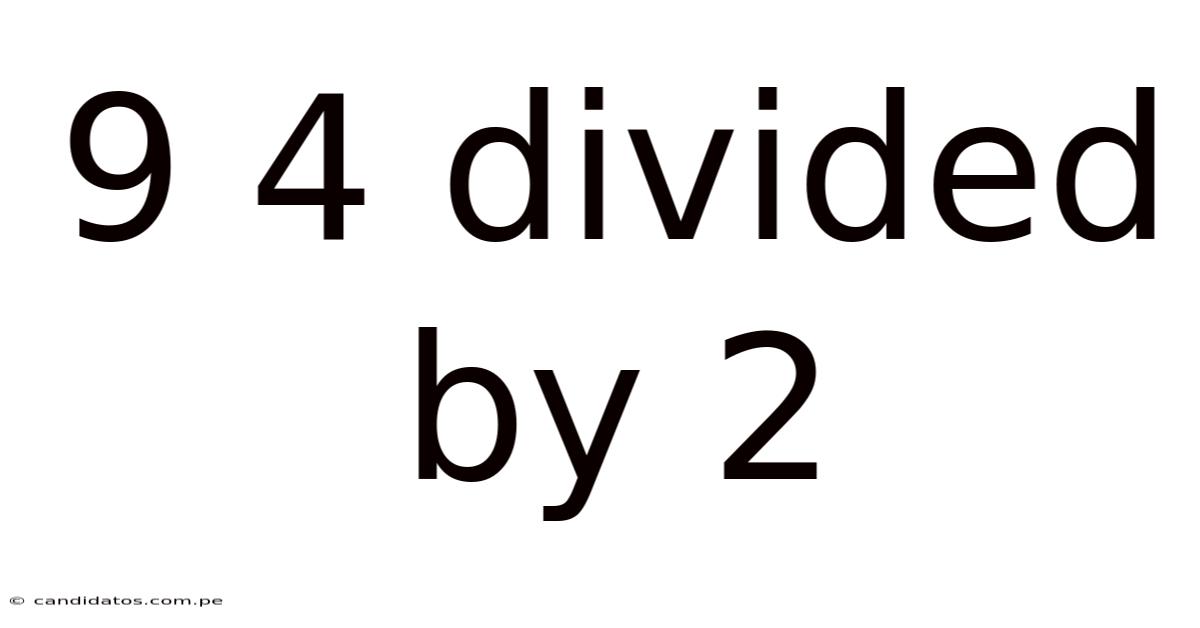
Table of Contents
Decoding 9/4 Divided by 2: A Deep Dive into Fractions and Division
This article explores the seemingly simple mathematical problem of 9/4 divided by 2, providing a comprehensive explanation suitable for learners of all levels. We'll break down the problem step-by-step, examining the underlying principles of fraction division and offering various approaches to solve it. Understanding this concept lays the groundwork for more advanced mathematical operations involving fractions and decimals. This guide will also address common misconceptions and answer frequently asked questions, solidifying your understanding of this fundamental concept.
Understanding Fractions: A Quick Refresher
Before tackling the division problem, let's quickly review the basics of fractions. A fraction represents a part of a whole. It's written as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates how many parts you have, while the denominator shows how many equal parts the whole is divided into. For example, in the fraction 9/4, 9 is the numerator and 4 is the denominator. This means we have 9 parts of a whole that's divided into 4 equal parts. This is an improper fraction because the numerator is larger than the denominator, indicating a value greater than 1.
Method 1: Dividing Fractions Using Reciprocal
The most common method for dividing fractions involves using the reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 2/3 is 3/2. To divide a fraction by another number, we change the division to multiplication by using the reciprocal of the divisor.
Here's how to apply this method to our problem, 9/4 divided by 2:
-
Rewrite the whole number as a fraction: We can rewrite 2 as the fraction 2/1. This makes the problem: 9/4 ÷ 2/1
-
Change division to multiplication using the reciprocal: The reciprocal of 2/1 is 1/2. So, the problem becomes: 9/4 x 1/2
-
Multiply the numerators and denominators: Multiply the numerators together (9 x 1 = 9) and the denominators together (4 x 2 = 8). This gives us the fraction 9/8.
-
Simplify (if possible): In this case, the fraction 9/8 is an improper fraction. We can convert it to a mixed number by dividing the numerator (9) by the denominator (8). 9 divided by 8 is 1 with a remainder of 1. Therefore, 9/8 can be written as 1 1/8.
Therefore, 9/4 divided by 2 equals 1 1/8.
Method 2: Converting to Decimals
Another approach is to convert the fraction to a decimal before performing the division. This method can be easier for some individuals, especially when dealing with more complex fractions.
-
Convert the fraction to a decimal: Divide the numerator (9) by the denominator (4): 9 ÷ 4 = 2.25
-
Divide the decimal by 2: Now divide the decimal result (2.25) by 2: 2.25 ÷ 2 = 1.125
Therefore, 9/4 divided by 2 equals 1.125. Note that 1.125 is the decimal equivalent of 1 1/8, confirming the result from Method 1.
Method 3: Visual Representation
Visualizing the problem can be beneficial, especially for beginners. Imagine you have 9 quarters (9/4, since a quarter is 1/4 of a dollar). Dividing these 9 quarters between 2 people means each person receives an equal share.
If you divide 9 quarters between 2 people, each person gets 4 quarters (which is 1 dollar), leaving 1 quarter remaining. This visually represents the solution of 1 1/8.
The Importance of Understanding Different Methods
Understanding multiple approaches to solving the same problem enhances your mathematical fluency. Each method highlights different aspects of fractions and division, offering a more holistic understanding of the concept. Choosing the method that works best for you depends on your personal preference and the complexity of the problem. For simple problems, converting to decimals might be quicker; for more complex problems, working with fractions directly might be more efficient.
Addressing Common Misconceptions
A common mistake is to simply divide the numerator by 2, ignoring the denominator. This incorrect approach would yield 9/4 ÷ 2 = 4.5/4, which is not the correct answer. Remember, division with fractions requires a different approach than simply dividing the individual parts of the fraction. Always apply the correct methods, such as using the reciprocal or converting to decimals, to accurately solve fraction division problems.
Extending the Concept: More Complex Fraction Division
The principles used to solve 9/4 divided by 2 can be extended to solve more complex fraction division problems. Consider the following example: (15/8) ÷ (3/4).
-
Find the reciprocal of the divisor (3/4): The reciprocal is 4/3.
-
Change division to multiplication: The problem becomes (15/8) x (4/3).
-
Simplify before multiplying (optional): Notice that 15 and 3 share a common factor of 3 (15/3 = 5 and 3/3 = 1). Also, 8 and 4 share a common factor of 4 (8/4 = 2 and 4/4 = 1). Simplifying before multiplication gives us (5/2) x (1/1) = 5/2.
-
Convert to a mixed number: 5/2 can be written as 2 1/2.
Therefore, (15/8) ÷ (3/4) = 2 1/2.
Frequently Asked Questions (FAQ)
-
Q: Why do we use the reciprocal when dividing fractions?
-
A: Dividing by a fraction is equivalent to multiplying by its reciprocal. This method arises from the definition of division and allows for a consistent and streamlined process for solving fraction division problems.
-
Q: Can I always convert fractions to decimals before dividing?
-
A: While this approach is often valid, it can sometimes lead to recurring decimals, making the calculation more complex. Working directly with fractions using the reciprocal method often provides a more straightforward solution, especially for fractions that result in non-terminating decimals.
-
Q: What if I get a negative fraction in the problem?
-
A: The principles remain the same, but pay close attention to the signs. Remember that a negative number divided by a positive number results in a negative number, and vice versa.
-
Q: How can I practice more fraction division problems?
-
A: Many online resources, textbooks, and educational websites provide practice problems for fraction division. Start with simple problems and gradually increase the complexity to build your confidence and skills.
Conclusion
Dividing fractions, even a seemingly simple problem like 9/4 divided by 2, requires a thorough understanding of fractions and division principles. By mastering the methods explained – using the reciprocal, converting to decimals, or even visualizing the problem – you can build a strong foundation in mathematics. Remember to practice regularly and to explore different methods to solidify your understanding. The ability to confidently work with fractions is crucial for success in more advanced mathematical concepts and applications. This comprehensive guide not only provides the answer but equips you with the tools and understanding to solve a wide range of fraction division problems.
Latest Posts
Latest Posts
-
5 Letter Words Ending Id
Sep 15, 2025
-
36 Out Of 40 Percentage
Sep 15, 2025
-
Words That Rhyme With Dignity
Sep 15, 2025
-
Characters That Start With R
Sep 15, 2025
-
5 2 On Number Line
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 9 4 Divided By 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.