9 13 As A Decimal
candidatos
Sep 15, 2025 · 6 min read
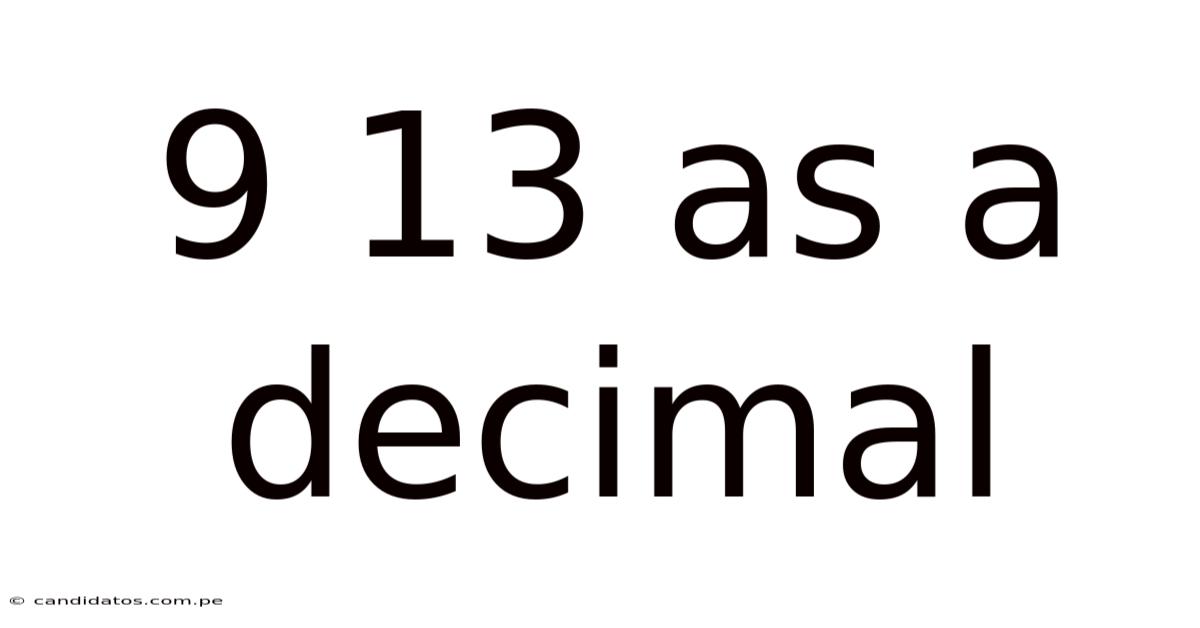
Table of Contents
9/13 as a Decimal: A Comprehensive Guide to Fraction-to-Decimal Conversion
Understanding how to convert fractions to decimals is a fundamental skill in mathematics. This comprehensive guide will delve into the process of converting the fraction 9/13 into its decimal equivalent, exploring various methods and addressing common questions. We'll not only find the decimal representation but also examine the underlying principles and applications of this conversion. This will equip you with a solid understanding of this crucial mathematical concept.
Understanding Fractions and Decimals
Before we dive into converting 9/13, let's briefly review the concepts of fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). A decimal, on the other hand, represents a fraction where the denominator is a power of 10 (e.g., 10, 100, 1000). Decimals use a decimal point to separate the whole number part from the fractional part.
For example, the fraction 1/2 is equivalent to the decimal 0.5, because half of one is represented as 0.5. Similarly, 3/4 is equivalent to 0.75, as three-quarters is 75 hundredths.
Method 1: Long Division
The most straightforward method for converting a fraction to a decimal is using long division. This involves dividing the numerator (9) by the denominator (13).
-
Set up the long division: Write 9 as the dividend (inside the division symbol) and 13 as the divisor (outside the division symbol). You'll need to add a decimal point and zeros to the dividend to continue the division until you reach a repeating pattern or a desired level of accuracy.
-
Divide: Begin dividing 9 by 13. Since 13 doesn't go into 9, you'll place a 0 in the quotient (the answer) and add a decimal point. Then, bring down a 0 to make 90.
-
Continue dividing: 13 goes into 90 six times (13 x 6 = 78). Subtract 78 from 90, leaving a remainder of 12.
-
Add zeros and continue: Bring down another zero to make 120. 13 goes into 120 nine times (13 x 9 = 117). Subtract 117 from 120, leaving a remainder of 3.
-
Repeating decimal: Bring down another zero to make 30. 13 goes into 30 twice (13 x 2 = 26). Subtract 26 from 30, leaving a remainder of 4. This process will continue, revealing a repeating pattern.
By continuing this process, you'll notice that the remainder will repeat, leading to a repeating decimal. The decimal representation of 9/13 is approximately 0.692307692307... This means the sequence "692307" repeats infinitely.
Method 2: Using a Calculator
A simpler, albeit less instructive method, is to use a calculator. Simply divide 9 by 13. Most calculators will display the decimal representation, often showing several decimal places. You'll still observe the repeating pattern, though the calculator might round off the result after a certain number of digits.
Using a calculator confirms the repeating decimal nature of 9/13: 0.692307692307...
Understanding Repeating Decimals
The result of 9/13 is a repeating decimal, also known as a recurring decimal. This means the decimal representation has a sequence of digits that repeats infinitely. We often denote repeating decimals using a bar above the repeating sequence. In this case, 9/13 can be represented as 0.692307̅ where the bar indicates that "692307" repeats indefinitely.
Understanding repeating decimals is crucial because many fractions result in such representations. This is different from terminating decimals, which have a finite number of digits after the decimal point (like 0.5 or 0.75).
Practical Applications and Significance
The conversion of fractions to decimals has numerous applications across various fields:
-
Engineering and Physics: Precise calculations in engineering and physics often require decimal representations for ease of computation and compatibility with digital systems.
-
Finance: Calculations involving percentages, interest rates, and financial modeling frequently utilize decimals.
-
Computer Science: Representing and manipulating numbers in computer systems often involve converting fractions to their decimal equivalents.
-
Everyday Calculations: While not always explicitly stated, decimals are integral to many everyday calculations, such as calculating discounts, determining unit prices, and understanding proportions.
Rounding Decimals
In many practical applications, it is necessary to round off a repeating decimal to a specific number of decimal places. The common rounding rules apply:
- Round down: If the digit following the desired decimal place is less than 5, the last digit remains the same.
- Round up: If the digit following the desired decimal place is 5 or greater, the last digit is increased by 1.
For example, rounding 9/13 to three decimal places would result in 0.692. Rounding to four decimal places would give 0.6923. The level of precision required depends on the context of the application.
Frequently Asked Questions (FAQ)
Q: Why does 9/13 result in a repeating decimal?
A: A fraction results in a repeating decimal if its denominator (in its simplest form) contains prime factors other than 2 and 5. Since 13 is a prime number other than 2 or 5, 9/13 results in a repeating decimal.
Q: Can all fractions be converted to decimals?
A: Yes, all fractions can be converted to decimals through long division. The resulting decimal will either be terminating or repeating.
Q: Is there a way to predict if a fraction will have a repeating or terminating decimal?
A: Yes. If the denominator of the fraction (in its simplest form) contains only prime factors of 2 and/or 5, the decimal will terminate. Otherwise, the decimal will repeat.
Q: What is the difference between a repeating and a non-repeating decimal?
A: A repeating decimal has a sequence of digits that repeat infinitely, while a non-repeating or terminating decimal has a finite number of digits after the decimal point.
Q: How many decimal places should I use when representing 9/13?
A: The number of decimal places you use depends on the required level of accuracy for your specific application. For most general purposes, using three or four decimal places (0.692 or 0.6923) provides sufficient accuracy. However, in scientific or engineering contexts, more decimal places might be necessary.
Conclusion
Converting fractions to decimals is a crucial skill with wide-ranging applications. We've explored multiple methods to convert the fraction 9/13 to its decimal equivalent, highlighting the concept of repeating decimals and their significance. Understanding these concepts and techniques will enhance your mathematical skills and provide a deeper appreciation for the relationship between fractions and decimals. Remember to choose the method that best suits your needs and always consider the appropriate level of decimal precision for your application. This understanding empowers you to tackle more complex mathematical problems confidently.
Latest Posts
Latest Posts
-
Fruits That Start With Z
Sep 15, 2025
-
Binomial Nomenclature For A Dog
Sep 15, 2025
-
Tons To Cubic Meters Conversion
Sep 15, 2025
-
Words That Start With Qa
Sep 15, 2025
-
Business Studies Syllabus Year 12
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 9 13 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.