8 Out Of 15 Percentage
candidatos
Sep 23, 2025 · 5 min read
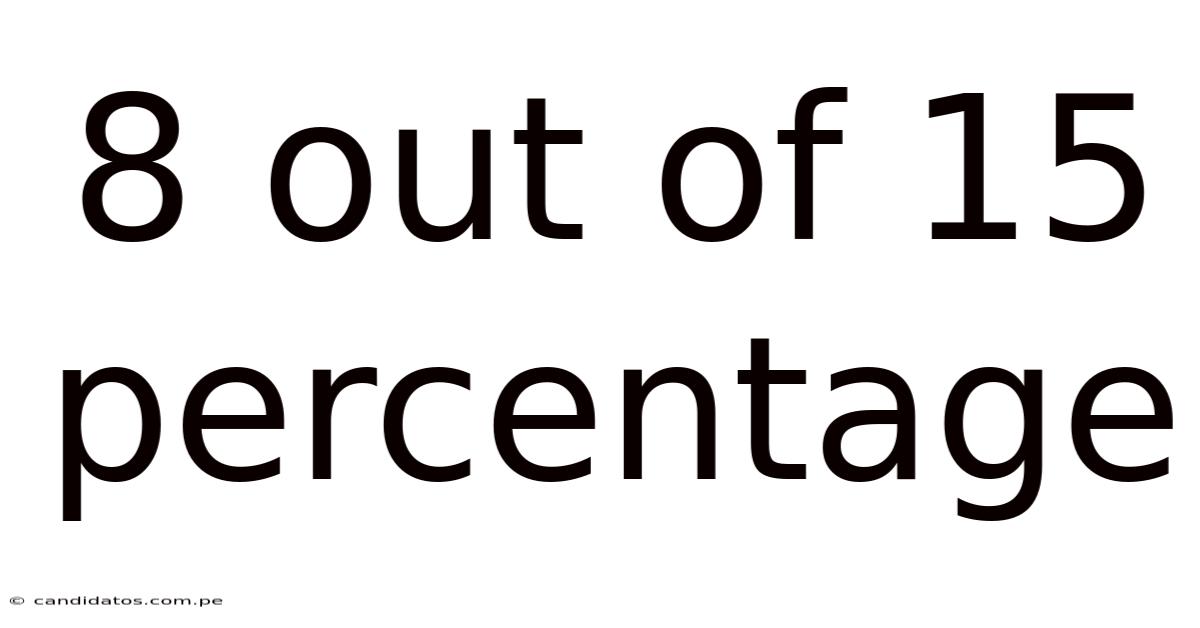
Table of Contents
Decoding 8 out of 15: Understanding Percentages and Their Applications
Understanding percentages is a fundamental skill applicable across numerous fields, from everyday finances to advanced scientific calculations. This article delves into the meaning of "8 out of 15," explains how to calculate percentages, explores its practical applications, and addresses common misconceptions. We'll unpack this seemingly simple concept to reveal its multifaceted nature and importance in various contexts. This comprehensive guide will empower you to confidently interpret and utilize percentage calculations in your daily life and beyond.
What Does 8 out of 15 Mean?
The phrase "8 out of 15" represents a fraction, specifically 8/15. This fraction indicates that 8 parts out of a total of 15 parts are being considered. To understand its significance, we need to convert this fraction into a percentage, which expresses the fraction as a proportion of 100. This conversion allows for easier comparison and interpretation of different proportions.
Calculating the Percentage: A Step-by-Step Guide
Converting 8/15 into a percentage involves a straightforward two-step process:
Step 1: Divide the numerator by the denominator.
In our example, we divide 8 (the numerator) by 15 (the denominator): 8 ÷ 15 = 0.5333...
Step 2: Multiply the result by 100 to express it as a percentage.
0.5333... × 100 = 53.33% (approximately)
Therefore, 8 out of 15 represents approximately 53.33%. The recurring decimal indicates that the percentage is an approximation; the exact value is a non-terminating decimal.
Understanding Percentage Accuracy and Rounding
It's crucial to understand that percentages often require rounding for practical purposes. While the exact value of 8/15 is 53.333..., we typically round this to 53.33% for clarity and ease of communication. The level of precision required depends on the context. In some situations, rounding to the nearest whole number (53%) might be sufficient, while in others, greater accuracy (53.33%) is necessary.
Practical Applications of Percentage Calculations
The ability to calculate and interpret percentages is essential in numerous real-world scenarios. Here are a few examples:
-
Academic Performance: If a student answers 8 out of 15 questions correctly on a test, their score is 53.33%. This allows for easy comparison of performance across different tests or students.
-
Sales and Discounts: A store offering a 20% discount on an item initially priced at $100 will reduce the price by $20 ($100 x 0.20 = $20), resulting in a final price of $80.
-
Financial Calculations: Interest rates, loan repayments, and investment returns are all expressed as percentages. Understanding these percentages is vital for making informed financial decisions.
-
Statistical Analysis: Percentages are fundamental in statistical analysis, allowing researchers to present data in a clear and concise manner, facilitating comparisons and interpretations of trends and patterns.
-
Scientific Research: Percentages are used to represent experimental results, error margins, and various other data points. This provides a standardized way of communicating and interpreting scientific findings.
-
Everyday Life: Calculating tips at restaurants, understanding sales tax, and figuring out proportions for recipes all involve percentage calculations.
Common Misconceptions about Percentages
Despite their seemingly simple nature, percentages can be prone to misinterpretations. Here are a few common misconceptions:
-
Confusing percentage change with percentage points: A change from 10% to 20% is a 100% increase, but it's also a 10 percentage point increase. The distinction is crucial for accurate interpretation.
-
Misinterpreting percentages without context: A percentage on its own is meaningless without understanding the context. For example, a 10% increase in sales is significant if the baseline is small but less impactful if the baseline is already large.
-
Incorrect application of percentages: Adding or subtracting percentages directly can lead to inaccurate results. For example, a 10% increase followed by a 10% decrease doesn't result in the original value.
Further Exploration of Percentages and Fractions
To deepen your understanding of percentages, exploring related concepts like fractions, ratios, and proportions is highly beneficial. Understanding how these concepts interconnect allows for a more holistic grasp of numerical relationships. Practicing various percentage calculation problems, ranging from simple to complex, is crucial for mastering the skill. The more you practice, the more comfortable you will become with interpreting and utilizing percentages in diverse scenarios.
Advanced Percentage Calculations: Beyond the Basics
While calculating simple percentages like 8 out of 15 is straightforward, more complex situations may arise. These often involve multiple percentages or changes over time.
-
Calculating percentage increase or decrease: This involves comparing two values and determining the percentage change between them. The formula is: [(New Value - Old Value) / Old Value] x 100.
-
Calculating percentage of a percentage: This involves finding a percentage of a value that is itself a percentage. For example, finding 15% of 20% of a certain number.
-
Compound interest calculations: This involves applying interest not only to the principal amount but also to accumulated interest. Understanding compound interest is crucial for long-term financial planning.
FAQ: Addressing Common Queries about Percentages
Q1: How do I calculate a percentage increase?
A1: To calculate a percentage increase, subtract the original value from the new value, divide the result by the original value, and multiply by 100.
Q2: How do I convert a decimal to a percentage?
A2: To convert a decimal to a percentage, multiply the decimal by 100 and add a "%" sign.
Q3: How do I convert a fraction to a percentage?
A3: To convert a fraction to a percentage, divide the numerator by the denominator, multiply the result by 100, and add a "%" sign.
Q4: What if I need to calculate a percentage of a very large number?
A4: The principles remain the same regardless of the number's size. Use a calculator or spreadsheet software for ease of calculation.
Conclusion: Mastering Percentages for a Brighter Future
Understanding percentages is not just about mastering a mathematical skill; it's about developing a crucial life skill applicable across numerous domains. From interpreting data in the news to making informed financial decisions, the ability to accurately calculate and interpret percentages empowers you to navigate the complexities of the modern world with confidence and clarity. By consistently practicing and applying the principles discussed in this article, you can confidently tackle percentage calculations and unlock a deeper understanding of the world around you. Remember, the journey to mastering percentages is iterative – practice regularly, and you'll steadily improve your proficiency and expand your capabilities.
Latest Posts
Latest Posts
-
Cardiac Muscle Under A Microscope
Sep 23, 2025
-
Location Crossword Clue 5 Letters
Sep 23, 2025
-
Birds That Have 5 Letters
Sep 23, 2025
-
Long Vowel E Sound Words
Sep 23, 2025
-
Transparent And Translucent And Opaque
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 8 Out Of 15 Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.