8 Divided By 1 3
candidatos
Sep 23, 2025 · 5 min read
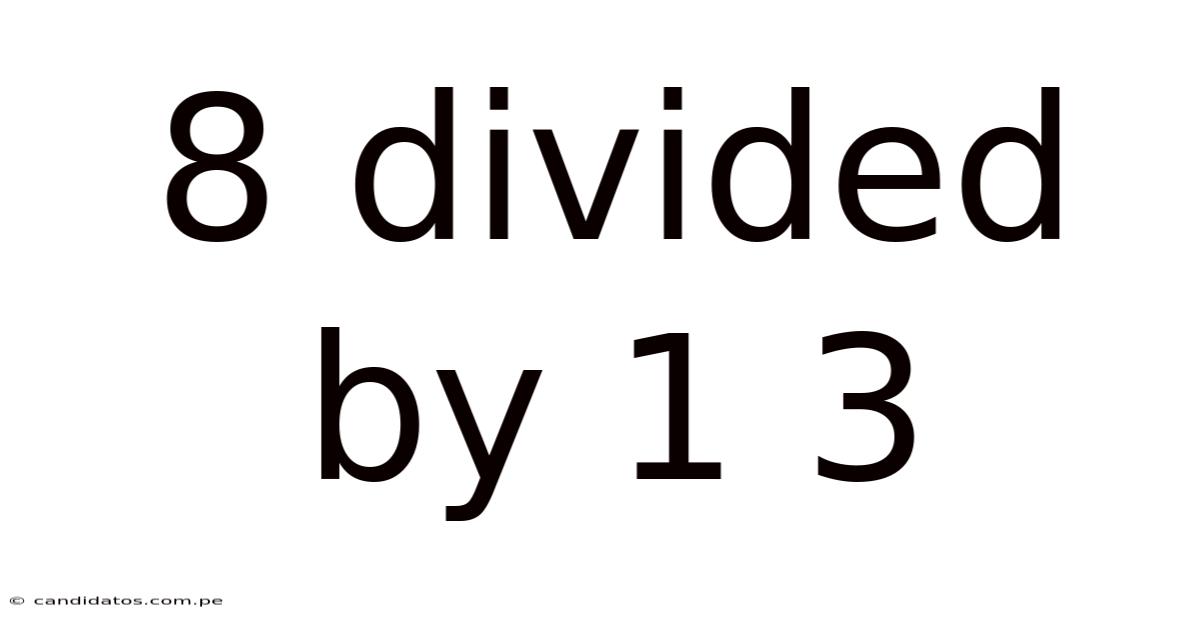
Table of Contents
8 Divided by 1⅓: A Deep Dive into Fraction Division
This article explores the seemingly simple problem of dividing 8 by 1⅓, providing a comprehensive guide for understanding the process, explaining the underlying mathematical principles, and offering practical applications. We'll move beyond a simple answer to delve into the why behind the calculations, making this concept clear for students of all levels, from elementary school to those brushing up on their math skills. This detailed explanation will cover various approaches to solving this problem, highlighting the flexibility and power of mathematical reasoning.
Understanding the Problem: 8 ÷ 1⅓
At its core, the problem "8 divided by 1⅓" asks: "How many times does 1⅓ fit into 8?" This seemingly straightforward question requires a grasp of fraction division, a crucial concept in mathematics. Many individuals struggle with fractions, and understanding division with fractions presents an additional layer of complexity. This article aims to demystify this process and build confidence in tackling similar problems.
Method 1: Converting to Improper Fractions
The most common and generally preferred method involves converting the mixed number (1⅓) into an improper fraction. This simplifies the division process significantly.
-
Step 1: Convert 1⅓ to an improper fraction. To do this, we multiply the whole number (1) by the denominator (3) and add the numerator (1). This sum (1*3 + 1 = 4) becomes the new numerator, while the denominator remains the same (3). Therefore, 1⅓ becomes ⁴⁄₃.
-
Step 2: Rewrite the division problem. The problem now reads: 8 ÷ ⁴⁄₃.
-
Step 3: Invert and multiply. Dividing by a fraction is equivalent to multiplying by its reciprocal (inverse). The reciprocal of ⁴⁄₃ is ³⁄₄. So, the problem transforms into: 8 x ³⁄₄.
-
Step 4: Simplify and solve. We can simplify before multiplying. 8 can be divided by 4, resulting in 2. The equation becomes: 2 x ³⁄₁ = ⁶⁄₁ = 6.
Therefore, 8 divided by 1⅓ equals 6.
Method 2: Using Decimal Equivalents
Another approach involves converting both numbers into decimals. This method is particularly helpful for those more comfortable with decimal arithmetic.
-
Step 1: Convert 1⅓ to a decimal. 1⅓ is equivalent to 1.333... (a repeating decimal). For practical purposes, we can use a close approximation, such as 1.33.
-
Step 2: Perform decimal division. Divide 8 by 1.33: 8 ÷ 1.33 ≈ 6.015.
This method yields an approximate answer due to the rounding of the decimal equivalent. While slightly less precise than the improper fraction method, it provides a valuable alternative for those who prefer working with decimals.
Method 3: Visual Representation
A visual approach can enhance understanding, especially for beginners. Imagine you have 8 identical units (e.g., pizzas, cakes). Each unit represents '1'. We need to determine how many groups of 1⅓ units we can make from these 8 units.
Imagine each group consisting of one whole unit and a third of another. You can easily create six full groups of 1⅓ units from the 8 units, using up (6 x 1⅓ = 8) units.
The Mathematical Principles Behind Fraction Division
The core principle behind dividing fractions lies in understanding the reciprocal. When dividing by a fraction, we're essentially asking: "How many times does this fraction fit into the whole number?" Inverting the fraction and multiplying allows us to find this answer efficiently. The process involves several key concepts:
-
Reciprocal (or multiplicative inverse): Two numbers are reciprocals if their product is 1. For example, the reciprocal of ⁴⁄₃ is ³⁄₄.
-
Fraction multiplication: Multiplying fractions involves multiplying the numerators together and the denominators together.
-
Equivalent fractions: Understanding equivalent fractions is crucial for simplification. We can simplify fractions by dividing both the numerator and denominator by their greatest common divisor.
Practical Applications
Understanding fraction division has numerous practical applications in various fields:
-
Cooking and Baking: Scaling recipes up or down frequently involves dividing fractions. If a recipe calls for 1⅓ cups of flour and you want to double it, you need to calculate 2 x 1⅓.
-
Construction and Engineering: Precise measurements in construction and engineering often involve fractions, necessitating division to determine the required amount of materials or the number of units needed.
-
Finance: Calculating proportions, interest rates, and shares often involves working with fractions and performing divisions.
-
Data Analysis: Interpreting data involving percentages and ratios necessitates a solid understanding of fraction division.
Frequently Asked Questions (FAQ)
Q1: Why do we invert and multiply when dividing fractions?
A1: Inverting and multiplying is a shortcut that stems from the definition of division. Dividing by a fraction is equivalent to multiplying by its reciprocal. This method simplifies the calculation process, making it more efficient.
Q2: What if the whole number was a fraction as well?
A2: If both numbers were fractions, you would still convert them to improper fractions, invert the second fraction, and multiply. The process remains the same.
Q3: What if I get a decimal answer instead of a whole number?
A3: A decimal answer is perfectly acceptable. It simply means that the divisor (1⅓) doesn't fit into the dividend (8) a whole number of times. The decimal represents the remaining fractional part.
Q4: Are there other methods to solve this problem?
A4: Yes, there are other methods, such as using long division with decimals or applying different fraction manipulation techniques. The methods presented here are among the most common and straightforward.
Conclusion: Mastering Fraction Division
Dividing 8 by 1⅓, while seemingly simple at first glance, presents an opportunity to solidify understanding of fraction division. By mastering this concept, you build a crucial foundation for tackling more complex mathematical problems in various fields. Remember that practicing different methods – converting to improper fractions, using decimals, and visualizing the problem – can help you develop a comprehensive understanding and build confidence in your mathematical abilities. Through consistent practice and exploring different approaches, you can overcome the challenges presented by fraction division and unlock a deeper appreciation for the elegance and power of mathematics. The key is to break down the problem into manageable steps and to understand the why behind each calculation, moving beyond simple memorization to true comprehension.
Latest Posts
Latest Posts
-
Cardiac Muscle Under A Microscope
Sep 23, 2025
-
Location Crossword Clue 5 Letters
Sep 23, 2025
-
Birds That Have 5 Letters
Sep 23, 2025
-
Long Vowel E Sound Words
Sep 23, 2025
-
Transparent And Translucent And Opaque
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 8 Divided By 1 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.