8 22 In Simplest Form
candidatos
Sep 20, 2025 · 5 min read
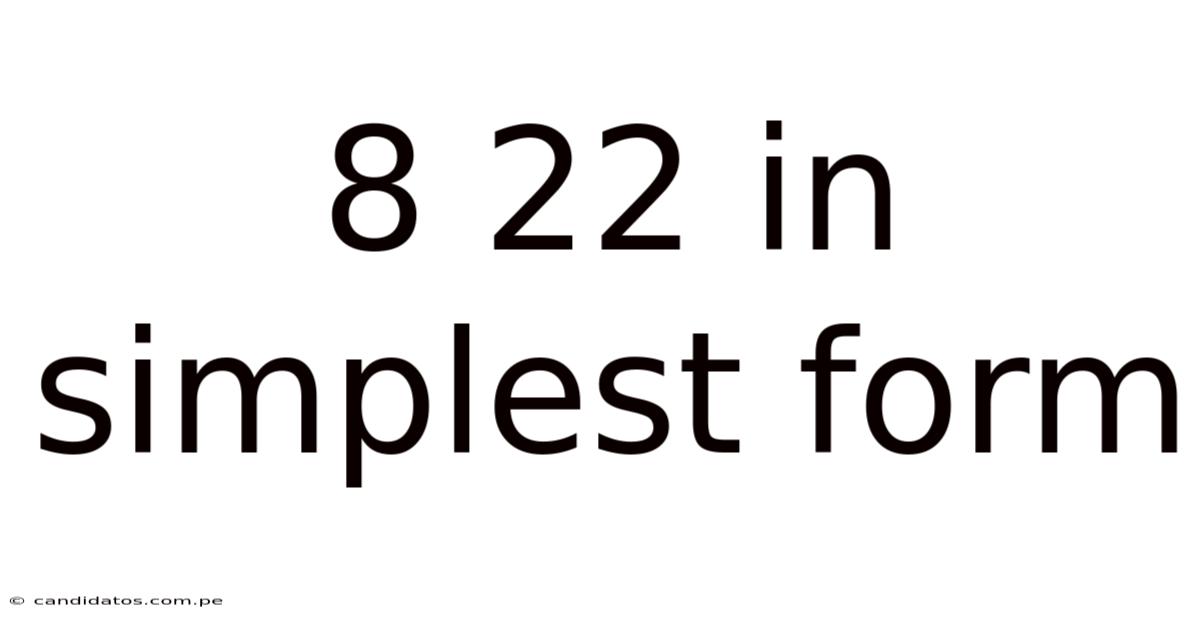
Table of Contents
Simplifying 8/22: A Comprehensive Guide to Fraction Reduction
Understanding how to simplify fractions is a fundamental skill in mathematics, essential for everything from basic arithmetic to advanced calculus. This article will delve into the process of simplifying the fraction 8/22, explaining the underlying principles and providing a step-by-step guide that even beginners can follow. We'll also explore related concepts and address common questions, ensuring a thorough understanding of fraction reduction.
Introduction:
The fraction 8/22 represents a part of a whole. To simplify a fraction means to express it in its lowest terms – a form where the numerator (top number) and the denominator (bottom number) share no common factors other than 1. This process is also known as reducing or expressing in simplest form. Learning to simplify fractions is crucial for making calculations easier and understanding the relationships between numbers more clearly. This guide will walk you through the simplification of 8/22 in a clear and concise manner, emphasizing the understanding behind the process rather than just rote memorization.
Understanding the Concept of Greatest Common Factor (GCF)
Before we begin simplifying 8/22, let's understand the core concept behind this process: the Greatest Common Factor (GCF). The GCF of two numbers is the largest number that divides both evenly (without leaving a remainder). Finding the GCF is the key to simplifying fractions efficiently.
To find the GCF of 8 and 22, we can use several methods:
-
Listing Factors: List all the factors of each number and identify the largest factor they share.
- Factors of 8: 1, 2, 4, 8
- Factors of 22: 1, 2, 11, 22
- The largest common factor is 2.
-
Prime Factorization: Break down each number into its prime factors (numbers divisible only by 1 and themselves). Then, identify the common prime factors and multiply them together.
- 8 = 2 x 2 x 2 = 2³
- 22 = 2 x 11
- The common prime factor is 2. Therefore, the GCF is 2.
Simplifying 8/22 Step-by-Step
Now that we know the GCF of 8 and 22 is 2, we can simplify the fraction:
-
Divide both the numerator and the denominator by the GCF: 8 ÷ 2 = 4 22 ÷ 2 = 11
-
Write the simplified fraction: The simplified form of 8/22 is 4/11.
Therefore, 8/22 in simplest form is 4/11. This means that 8/22 and 4/11 represent the same proportion or part of a whole.
Visual Representation
Imagine you have a pizza cut into 22 slices. 8/22 means you have 8 out of those 22 slices. If you group the slices into pairs (because the GCF is 2), you'll have 4 pairs of slices out of 11 pairs of slices. This visually demonstrates that 8/22 is equivalent to 4/11.
Why Simplify Fractions?
Simplifying fractions offers several advantages:
-
Easier Calculations: Working with smaller numbers makes calculations significantly easier. For example, adding 4/11 and 2/11 is much simpler than adding 8/22 and 4/22.
-
Clearer Understanding: Simplified fractions provide a clearer understanding of the proportion or ratio represented. 4/11 immediately communicates a more precise relationship than 8/22.
-
Standard Form: Presenting answers in simplest form is a standard practice in mathematics, ensuring consistency and ease of communication.
Further Exploration: Working with Larger Numbers
The process remains the same even with larger numbers. Let's consider simplifying a more complex fraction, say 48/72.
-
Find the GCF: Using prime factorization: 48 = 2 x 2 x 2 x 2 x 3 = 2⁴ x 3 72 = 2 x 2 x 2 x 3 x 3 = 2³ x 3² The common prime factors are 2³ and 3. Therefore, the GCF is 2³ x 3 = 8 x 3 = 24.
-
Divide: 48 ÷ 24 = 2 72 ÷ 24 = 3
-
Simplified Fraction: 48/72 simplifies to 2/3.
Dealing with Improper Fractions
An improper fraction is one where the numerator is greater than or equal to the denominator (e.g., 11/4). While simplifying an improper fraction follows the same GCF principle, it's often beneficial to convert it to a mixed number (a whole number and a fraction) after simplification for clarity.
For example, let's simplify 24/18:
-
Find the GCF: The GCF of 24 and 18 is 6.
-
Divide: 24 ÷ 6 = 4 18 ÷ 6 = 3
-
Simplified Fraction: 24/18 simplifies to 4/3.
-
Convert to Mixed Number: 4/3 is an improper fraction. Dividing 4 by 3 gives 1 with a remainder of 1. Therefore, 4/3 is equivalent to 1 1/3.
Frequently Asked Questions (FAQ)
-
Q: What if the GCF is 1?
- A: If the GCF of the numerator and denominator is 1, the fraction is already in its simplest form. It cannot be simplified further.
-
Q: Can I simplify a fraction by dividing the numerator and denominator by different numbers?
- A: No. To maintain the value of the fraction, you must divide both the numerator and denominator by the same number (the GCF).
-
Q: Is there a quick way to find the GCF?
- A: While prime factorization is reliable, for smaller numbers, you can often visually identify the GCF by quickly listing factors. Calculators and online tools can also calculate the GCF for larger numbers.
-
Q: What if the fraction involves decimals or negative numbers?
- A: For fractions with decimals, convert them to fractions first. For fractions involving negative numbers, remember that a negative divided by a negative is positive, and a negative divided by a positive is negative. Simplify the absolute values and then apply the appropriate sign.
Conclusion:
Simplifying fractions is a fundamental skill in mathematics. By understanding the concept of the Greatest Common Factor and following the steps outlined in this guide, you can confidently simplify any fraction, regardless of its complexity. Remember, the goal is to express the fraction in its lowest terms, making calculations easier and fostering a deeper understanding of numerical relationships. Practice is key to mastering this skill, so work through various examples to build your confidence and proficiency. The ability to simplify fractions will serve as a strong foundation for your future mathematical endeavors.
Latest Posts
Latest Posts
-
Direct Variation Vs Inverse Variation
Sep 20, 2025
-
Words That Start With So
Sep 20, 2025
-
Number Of The Day Worksheet
Sep 20, 2025
-
Worksheet On Addition With Regrouping
Sep 20, 2025
-
500 Spelling Bee Words Pdf
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 8 22 In Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.