7 Out Of 20 Percentage
candidatos
Sep 18, 2025 · 5 min read
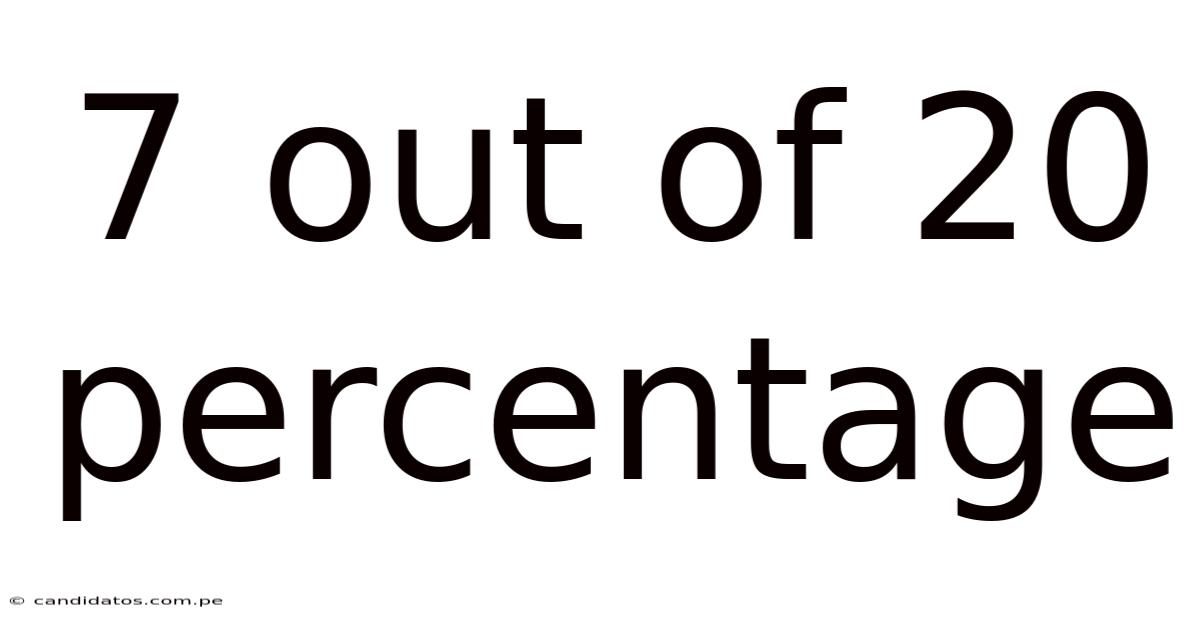
Table of Contents
Understanding 7 out of 20: A Comprehensive Guide to Percentages, Fractions, and Decimals
Calculating percentages is a fundamental skill applicable in numerous areas of life, from everyday budgeting and shopping to advanced scientific calculations and financial analysis. Understanding how to represent a portion of a whole is crucial, and this article will delve into the specific example of "7 out of 20," exploring its representation as a fraction, decimal, and percentage, along with broader applications and common misconceptions. This guide aims to equip you with a comprehensive understanding of this seemingly simple calculation and its broader implications.
Understanding Fractions: The Foundation of Percentages
Before we dive into the specifics of 7 out of 20, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates the number of parts we have, and the denominator indicates the total number of parts that make up the whole.
In our case, "7 out of 20" is a fraction where:
- Numerator (7): Represents the number of parts we're interested in.
- Denominator (20): Represents the total number of parts.
Therefore, the fraction representing "7 out of 20" is 7/20.
Converting Fractions to Decimals: A Step-by-Step Process
To convert a fraction to a decimal, we simply divide the numerator by the denominator. For 7/20, the calculation is as follows:
7 ÷ 20 = 0.35
Therefore, the decimal representation of 7/20 is 0.35. This means that 7 out of 20 represents 35 hundredths of the whole.
Converting Fractions and Decimals to Percentages: The Percentage Formula
A percentage is a way of expressing a fraction or decimal as a portion of 100. To convert a fraction or decimal to a percentage, we multiply the decimal value by 100 and add the "%" symbol.
Using our example:
0.35 x 100 = 35%
Therefore, 7 out of 20 is equivalent to 35%. This indicates that 7 represents 35% of the total 20 parts.
Visualizing 7 out of 20: A Pictorial Representation
Visualizing the fraction can make it easier to understand. Imagine a pie chart divided into 20 equal slices. Seven of those slices represent 7 out of 20. This visual representation reinforces the concept of a part relative to the whole.
Practical Applications of 7 out of 20 (35%)
The ability to understand and calculate percentages like 35% has numerous real-world applications:
- Grade Calculation: If a student answers 7 out of 20 questions correctly on a test, their score is 35%.
- Sales and Discounts: A 35% discount on an item means the price is reduced by 35% of the original price.
- Financial Analysis: Analyzing financial statements often involves calculating percentages to understand profit margins, growth rates, or debt levels. For example, a company might report that 35% of its revenue comes from a specific product line.
- Statistical Analysis: Percentages are frequently used to present data in a clear and concise manner, allowing for easy comparison and interpretation. For instance, a survey might show that 35% of respondents prefer a particular product.
- Probability and Odds: In probability, percentages are used to express the likelihood of an event occurring. If the probability of an event is 35%, it means there's a 35% chance that the event will happen.
Working with Larger Numbers: Scaling the Calculation
While we've focused on 7 out of 20, the principles remain the same when dealing with larger numbers. Let's consider a scenario where a student answers 70 out of 200 questions correctly. The fraction is 70/200. We can simplify this fraction by dividing both the numerator and denominator by their greatest common divisor (GCD), which is 10:
70/200 simplifies to 7/20. As we've already established, 7/20 = 0.35 = 35%.
This demonstrates that the percentage remains consistent even when the numbers are scaled up proportionally.
Common Misconceptions about Percentages
Several common misconceptions can lead to errors in percentage calculations:
- Confusing Percentage with Absolute Value: A percentage represents a proportion, not an absolute quantity. A 35% increase in sales might represent a significantly different number of units sold depending on the initial sales volume.
- Incorrectly Calculating Percentage Change: Calculating percentage changes requires care. The percentage change is calculated as [(New Value - Old Value) / Old Value] x 100. Simply subtracting the two values and expressing it as a percentage is incorrect.
- Ignoring Base Value: The base value (the denominator in the fraction) is crucial. Saying something increased by 35% without specifying the base value is meaningless.
Frequently Asked Questions (FAQs)
Q: How do I calculate a percentage of a number?
A: To calculate a percentage of a number, convert the percentage to a decimal by dividing by 100 and then multiply the decimal by the number. For example, 35% of 100 is (35/100) x 100 = 35.
Q: What if I have a percentage and want to find the original value?
A: This requires working backward. If you know that 35% of a number is x, you can set up an equation: 0.35 * original number = x. Solve for the original number by dividing x by 0.35.
Q: Can I use a calculator for percentage calculations?
A: Yes, most calculators have percentage functions that simplify these calculations.
Conclusion: Mastering Percentages for Everyday Success
Understanding how to calculate and interpret percentages is a valuable life skill. This article has provided a comprehensive explanation of the concept, using the example of 7 out of 20 to illustrate the process of converting between fractions, decimals, and percentages. By mastering these fundamental concepts, you'll be better equipped to handle various real-world scenarios involving proportions, ratios, and statistical analysis, improving your ability to analyze data, make informed decisions, and achieve your goals. Remember to always pay attention to the context and avoid common misconceptions to ensure accuracy in your calculations.
Latest Posts
Latest Posts
-
Words That End With Ee
Sep 18, 2025
-
33 45 As A Percentage
Sep 18, 2025
-
Linear Expansion Coefficient For Steel
Sep 18, 2025
-
36 45 As A Percentage
Sep 18, 2025
-
Inverted Commas And Full Stops
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 7 Out Of 20 Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.