7 9 X 7 9
candidatos
Sep 19, 2025 · 5 min read
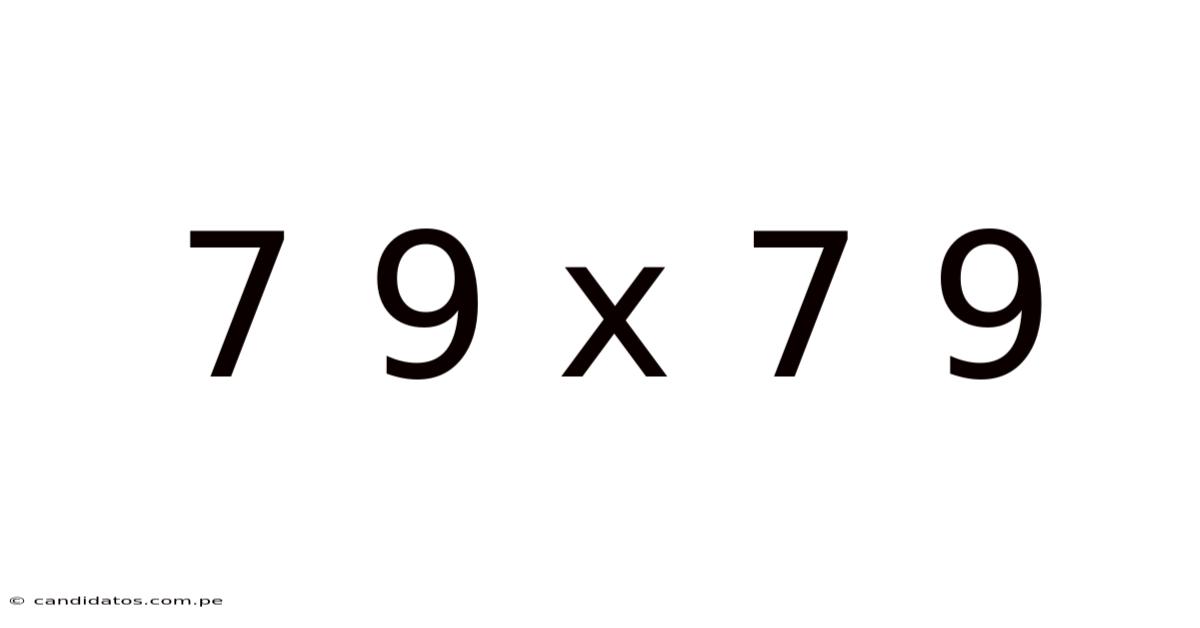
Table of Contents
Decoding the Mystery: A Deep Dive into 79 x 79
The seemingly simple multiplication problem, 79 x 79, can open a door to a surprisingly rich understanding of mathematics. This article will not only solve this specific problem but delve into various methods to approach it, exploring underlying mathematical principles and showcasing the beauty and elegance inherent in arithmetic. We'll examine traditional methods, explore shortcuts, and even touch upon the historical context of multiplication. By the end, you'll not only know the answer to 79 x 79 but will also possess a deeper appreciation for the power and versatility of mathematical operations.
Understanding the Fundamentals: Traditional Multiplication
Let's start with the most fundamental method: standard long multiplication. This method, taught in elementary schools worldwide, provides a solid foundation for understanding how multiplication works.
Step-by-Step Breakdown:
-
Set up the problem: Write the numbers vertically, one above the other, aligning the units digits.
79 x 79 ---- -
Multiply by the units digit: Multiply 79 by the units digit of 79 (which is 9).
79 x 79 ---- 711 (9 x 79) -
Multiply by the tens digit: Multiply 79 by the tens digit of 79 (which is 7), remembering to add a zero as a placeholder in the units column because we're multiplying by 70, not 7.
79 x 79 ---- 711 5530 (70 x 79) -
Add the partial products: Add the two partial products together.
79 x 79 ---- 711 5530 ---- 6241
Therefore, 79 x 79 = 6241.
Exploring Alternative Methods: The Power of Mental Math
While the long multiplication method is reliable, it's not always the most efficient. Let's explore some alternative approaches that can be used to solve 79 x 79 mentally or with minimal written calculations.
Method 1: Difference of Squares
This method leverages the algebraic identity (a+b)(a-b) = a² - b². We can rewrite 79 as (80 - 1). Then, 79 x 79 becomes (80 - 1)(80 - 1). This can be expanded as:
(80 - 1)² = 80² - 2(80)(1) + 1² = 6400 - 160 + 1 = 6241
This method is particularly useful for numbers close to multiples of 10.
Method 2: Distributive Property
We can use the distributive property to break down the problem:
79 x 79 = 79 x (80 - 1) = (79 x 80) - (79 x 1) = 6320 - 79 = 6241
This method offers a slightly different approach to the difference of squares but relies on the same fundamental mathematical principle.
A Deeper Dive: The Mathematical Concepts at Play
The seemingly simple calculation of 79 x 79 involves several fundamental mathematical concepts:
-
Multiplication: The foundation of the problem itself. Multiplication is repeated addition. 79 x 79 means adding 79 to itself 79 times.
-
Distributive Property: This property states that a(b + c) = ab + ac. This is crucial in the alternative methods discussed above, allowing us to break down the multiplication into smaller, more manageable steps.
-
Exponents: The difference of squares method utilizes the concept of exponents (specifically, squaring a number). Understanding exponents is essential for efficient calculations, particularly with larger numbers.
-
Place Value: In long multiplication, understanding place value is crucial for correctly aligning the partial products and adding them accurately. The value of a digit depends on its position in the number.
-
Number Properties: The commutative property (a x b = b x a) allows us to reverse the order of the numbers without changing the product. This may seem trivial but is a fundamental property used implicitly in many calculations.
Historical Context: The Evolution of Multiplication
The methods we use today for multiplication are the result of centuries of mathematical development. Ancient civilizations developed various methods for multiplication, often utilizing different tools and techniques. The Egyptians used a doubling method, while the Babylonians utilized a sexagesimal system (base 60). The development of algorithms, like the long multiplication we use, was a significant advancement in simplifying complex calculations. The invention of the abacus and later calculators revolutionized how we approach multiplication. Understanding this historical context highlights the evolution of mathematical thinking and how our methods have become increasingly efficient and streamlined over time.
Beyond 79 x 79: Extending the Concepts
The techniques used to solve 79 x 79 can be applied to a wide range of multiplication problems. The difference of squares method is especially useful for numbers close to multiples of 10, 100, or 1000. The distributive property can be used to simplify more complex multiplications involving multiple terms. Mastering these techniques fosters mathematical fluency and problem-solving skills applicable far beyond this single example.
Frequently Asked Questions (FAQs)
Q: What is the easiest way to multiply 79 by 79?
A: The easiest method depends on your comfort level with different mathematical approaches. If you prefer a systematic approach, long multiplication is reliable. For mental calculation, the difference of squares method or the distributive property can be quicker.
Q: Are there other methods to solve this multiplication problem?
A: Yes, there are numerous methods. Some involve using grids, or even employing lattice multiplication, a historical method which visually organizes the multiplication process. Calculators provide the most immediate answer, but understanding the underlying principles remains crucial for mathematical proficiency.
Q: Why is understanding the underlying mathematical concepts important?
A: Understanding the underlying concepts, like the distributive property and the difference of squares, is vital for building mathematical intuition and problem-solving skills. These concepts apply to various mathematical areas, making you a more versatile and resourceful problem solver.
Q: How can I improve my multiplication skills?
A: Practice is key. Regular practice with different multiplication problems, using various methods, will enhance your speed and accuracy. Try solving problems mentally before resorting to written calculations. Exploring different methods and understanding their underlying principles will deepen your understanding and improve your overall mathematical abilities.
Conclusion: More Than Just a Number
The seemingly simple calculation of 79 x 79 opens a gateway to a vast world of mathematical concepts and techniques. By exploring different methods and understanding the underlying principles, we not only arrive at the answer (6241) but also cultivate a deeper appreciation for the beauty and elegance of mathematics. This problem serves as a microcosm of mathematical thinking, highlighting the power of efficient methods, the importance of fundamental concepts, and the rich history behind the arithmetic we use every day. Hopefully, this exploration has not only provided the answer but also fostered a greater understanding and appreciation for the fascinating world of numbers.
Latest Posts
Latest Posts
-
How Many Neutrons In K
Sep 19, 2025
-
1 Litre How Many Grams
Sep 19, 2025
-
Tiny Things Studied By Chemists
Sep 19, 2025
-
Diagram Of Wastewater Treatment Plant
Sep 19, 2025
-
Picture Of A Synovial Joint
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 7 9 X 7 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.