7 12 Minus 1 3
candidatos
Sep 17, 2025 · 5 min read
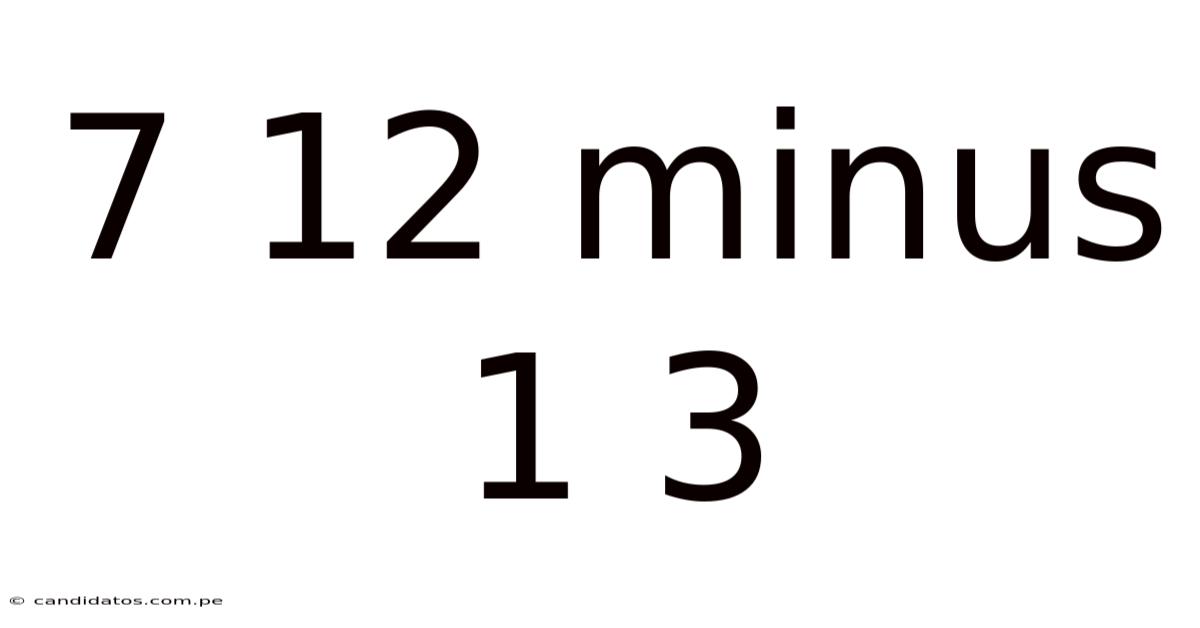
Table of Contents
Decoding 7 1/2 Minus 1 1/3: A Comprehensive Guide to Mixed Number Subtraction
This article provides a comprehensive explanation of how to subtract mixed numbers, specifically focusing on the calculation 7 1/2 - 1 1/3. We'll break down the process step-by-step, explore the underlying mathematical principles, and address frequently asked questions. This guide aims to build a strong understanding of mixed number subtraction, empowering you to confidently tackle similar problems. Understanding this seemingly simple calculation unlocks a deeper understanding of fractions and their manipulation in arithmetic.
Introduction: Understanding Mixed Numbers
Before diving into the subtraction, let's refresh our understanding of mixed numbers. A mixed number combines a whole number and a fraction. For example, 7 1/2 represents seven whole units and one-half of another unit. Understanding the components of a mixed number is crucial for performing operations like subtraction. We can also represent mixed numbers as improper fractions, where the numerator is larger than the denominator. This representation will prove useful in our calculation.
Converting Mixed Numbers to Improper Fractions: The Crucial First Step
Subtracting mixed numbers directly can be challenging. The most efficient approach involves converting them into improper fractions. An improper fraction is a fraction where the numerator is greater than or equal to the denominator. Let's convert both our mixed numbers:
-
7 1/2: To convert this to an improper fraction, we multiply the whole number (7) by the denominator (2), add the numerator (1), and keep the same denominator (2). This gives us (7 * 2 + 1)/2 = 15/2.
-
1 1/3: Similarly, we convert 1 1/3 to an improper fraction: (1 * 3 + 1)/3 = 4/3.
Now our subtraction problem becomes 15/2 - 4/3. This is a much more manageable form.
Finding a Common Denominator: The Key to Subtraction
To subtract fractions, they must share a common denominator. In our case, the denominators are 2 and 3. The least common multiple (LCM) of 2 and 3 is 6. This means we need to convert both fractions to have a denominator of 6.
-
15/2: To change the denominator to 6, we multiply both the numerator and the denominator by 3: (15 * 3) / (2 * 3) = 45/6.
-
4/3: To change the denominator to 6, we multiply both the numerator and the denominator by 2: (4 * 2) / (3 * 2) = 8/6.
Now our subtraction problem is simplified to 45/6 - 8/6.
Performing the Subtraction: A Simple Operation
With a common denominator, subtracting the fractions is straightforward: We subtract the numerators and keep the same denominator.
45/6 - 8/6 = (45 - 8)/6 = 37/6
Converting Back to a Mixed Number: Expressing the Result Clearly
Our answer, 37/6, is an improper fraction. To express it as a mixed number (which is often preferred for clarity), we perform division:
37 divided by 6 is 6 with a remainder of 1. This means our answer is 6 and 1/6.
Therefore, 7 1/2 - 1 1/3 = 6 1/6.
A Deeper Dive into the Mathematical Principles
The process we've followed is based on fundamental principles of fraction arithmetic. The core concepts include:
-
Equivalent Fractions: Multiplying or dividing both the numerator and denominator of a fraction by the same non-zero number results in an equivalent fraction. This is crucial for finding common denominators.
-
Least Common Multiple (LCM): Finding the LCM of the denominators ensures we use the smallest possible common denominator, simplifying the calculations.
-
Fraction Addition and Subtraction: When adding or subtracting fractions with a common denominator, we add or subtract the numerators and retain the common denominator.
-
Improper Fractions and Mixed Numbers: Understanding the conversion between these two forms is vital for efficient calculations.
Step-by-Step Summary: 7 1/2 - 1 1/3
To summarize the entire process, here's a concise step-by-step guide:
-
Convert Mixed Numbers to Improper Fractions: 7 1/2 becomes 15/2 and 1 1/3 becomes 4/3.
-
Find a Common Denominator: The LCM of 2 and 3 is 6.
-
Convert Fractions to Common Denominator: 15/2 becomes 45/6 and 4/3 becomes 8/6.
-
Subtract the Fractions: 45/6 - 8/6 = 37/6.
-
Convert the Result to a Mixed Number (optional): 37/6 = 6 1/6.
Frequently Asked Questions (FAQ)
Q: Can I subtract mixed numbers without converting to improper fractions?
A: While possible, it's generally more complex and prone to errors. Converting to improper fractions provides a more systematic and straightforward approach.
Q: What if the fractions have different denominators that don't share a common factor?
A: You still need to find a common denominator. In such cases, simply multiply the denominators to find a common denominator (though not necessarily the least common denominator).
Q: What if I get a negative result after subtracting the numerators?
A: This indicates the second mixed number is larger than the first. You'll have a negative improper fraction, which you can then convert to a mixed number with a negative whole number part.
Q: Are there other methods for subtracting mixed numbers?
A: Yes, some people prefer to subtract the whole numbers and the fractional parts separately, then combine the results. However, this method requires careful handling of borrowing from the whole number part if the fractional part of the subtrahend is larger than the fractional part of the minuend, making it less efficient than the improper fraction method.
Q: How can I check my answer?
A: You can estimate the answer by rounding the mixed numbers to the nearest whole number. For example, 7 1/2 is close to 7, and 1 1/3 is close to 1. 7 - 1 = 6, so our answer of 6 1/6 is reasonable. You can also convert your answer back to an improper fraction and perform the subtraction in the opposite order to verify the result.
Conclusion: Mastering Mixed Number Subtraction
Subtracting mixed numbers might seem daunting at first, but breaking down the process into manageable steps – converting to improper fractions, finding a common denominator, and performing the subtraction – makes it significantly easier. By understanding the underlying mathematical principles and practicing these steps, you'll build confidence and proficiency in tackling mixed number subtraction problems, opening doors to more advanced mathematical concepts. This methodical approach not only provides the correct answer but also fosters a deeper understanding of fractional arithmetic. Remember, practice is key! The more you work with mixed numbers and fractions, the more comfortable and fluent you'll become.
Latest Posts
Latest Posts
-
When Is Hsc Exam 2024
Sep 17, 2025
-
Is The Haber Process Exothermic
Sep 17, 2025
-
Biology Unit 3 And 4
Sep 17, 2025
-
Partnership Business Advantages And Disadvantages
Sep 17, 2025
-
Words That Rhyme With Longer
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 7 12 Minus 1 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.