60 65 As A Percentage
candidatos
Sep 19, 2025 · 5 min read
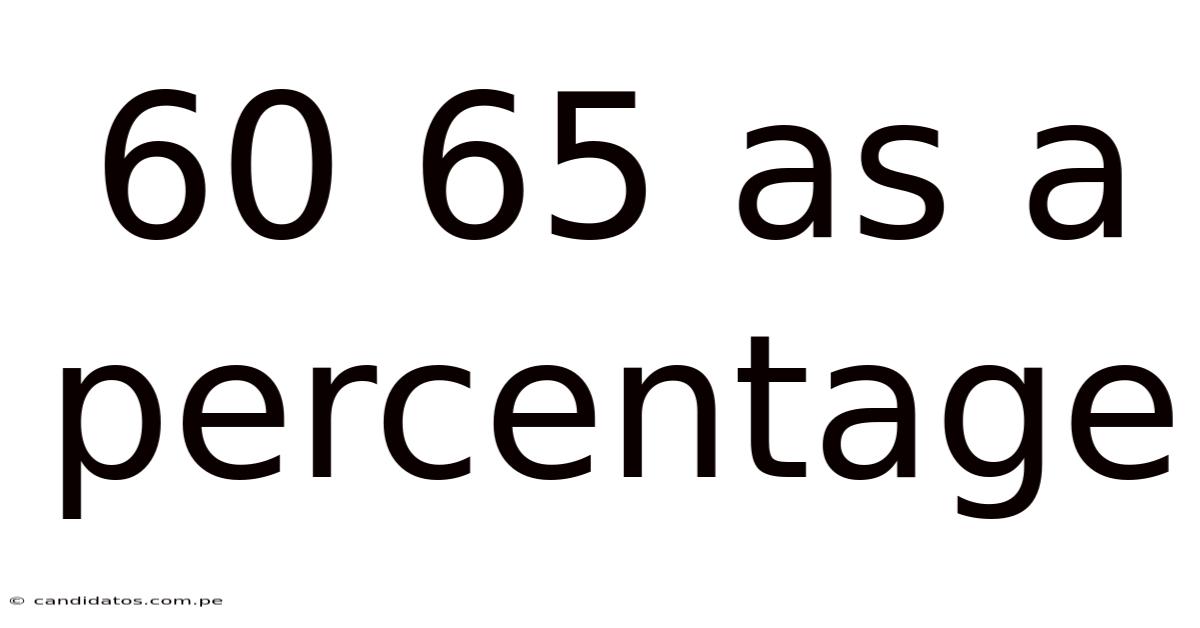
Table of Contents
60 out of 65 as a Percentage: A Comprehensive Guide
Understanding percentages is a fundamental skill in many aspects of life, from calculating discounts in shopping to analyzing data in professional settings. This article delves into the process of converting a fraction, such as 60 out of 65, into a percentage, exploring the underlying mathematical principles and providing practical examples. We'll also look at different methods for calculating percentages and address frequently asked questions. This guide aims to equip you with a thorough understanding of percentage calculations, empowering you to confidently tackle similar problems in the future.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred." Therefore, when we say 50%, we mean 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5. Percentages are incredibly useful for comparing different proportions and making relative comparisons easier to understand.
Calculating 60 out of 65 as a Percentage: Method 1 - The Fraction Method
The most straightforward method involves expressing the given numbers as a fraction and then converting that fraction into a percentage.
-
Form a fraction: Represent "60 out of 65" as a fraction: 60/65.
-
Simplify the fraction (optional): While not strictly necessary, simplifying the fraction makes the subsequent calculations easier. Both 60 and 65 are divisible by 5, resulting in the simplified fraction 12/13.
-
Convert the fraction to a decimal: Divide the numerator (12) by the denominator (13): 12 ÷ 13 ≈ 0.923
-
Convert the decimal to a percentage: Multiply the decimal by 100 and add the "%" symbol: 0.923 × 100 ≈ 92.3%
Therefore, 60 out of 65 is approximately 92.3%.
Calculating 60 out of 65 as a Percentage: Method 2 - The Direct Proportion Method
This method uses the concept of direct proportion to calculate the percentage directly.
-
Set up a proportion: We want to find the percentage x such that:
60/65 = x/100
-
Cross-multiply: This gives us:
65x = 6000
-
Solve for x: Divide both sides by 65:
x = 6000/65 ≈ 92.3
-
Express as a percentage: Therefore, x ≈ 92.3%.
Again, we find that 60 out of 65 is approximately 92.3%.
Understanding the Approximation
It's important to note that the result, 92.3%, is an approximation. The decimal representation of 12/13 is a non-terminating decimal (it goes on forever without repeating). We have rounded the decimal to three decimal places for practical purposes. The higher the number of decimal places you use, the more precise your percentage will be. For most practical applications, however, rounding to one or two decimal places is sufficient.
Practical Applications of Percentage Calculations
The ability to calculate percentages is valuable in a wide range of situations, including:
-
Academic Performance: Calculating grades based on marks obtained. For instance, if a student scores 60 out of 65 in a test, their percentage score is 92.3%, a good indicator of their performance.
-
Financial Calculations: Determining interest rates, discounts, tax amounts, profit margins, and more. Understanding percentage changes in investments is crucial for financial planning.
-
Data Analysis: Representing data in a clear and concise way. Percentages are often used in charts and graphs to illustrate proportions and trends.
-
Sales and Marketing: Calculating sales growth, conversion rates, and customer acquisition costs. Understanding percentages is essential for businesses to track their performance and make informed decisions.
-
Everyday Life: Calculating tips, discounts at stores, and understanding proportions in recipes.
Further Exploring Percentages: Percentage Increase and Decrease
Beyond simple percentage calculations, we often need to determine percentage increases or decreases. For example, if a price increases from 60 to 65, we would calculate the percentage increase.
-
Find the difference: 65 - 60 = 5
-
Divide the difference by the original value: 5 / 60 ≈ 0.0833
-
Multiply by 100 to get the percentage: 0.0833 × 100 ≈ 8.33%
Therefore, the price increased by approximately 8.33%.
Similarly, if the price decreased from 65 to 60, we'd calculate the percentage decrease using the same method, but using the original value of 65:
-
Find the difference: 65 - 60 = 5
-
Divide the difference by the original value: 5 / 65 ≈ 0.0769
-
Multiply by 100 to get the percentage: 0.0769 × 100 ≈ 7.69%
Therefore, the price decreased by approximately 7.69%.
Frequently Asked Questions (FAQ)
Q: What if I need a more precise answer than 92.3%?
A: You can increase the number of decimal places in your calculations. Instead of rounding to three decimal places, you could use more, depending on the required level of accuracy. Calculators and spreadsheet software can handle this easily. Using a calculator or software provides higher precision than manual calculation.
Q: Can I use a calculator to solve this?
A: Absolutely! Calculators and spreadsheet programs (like Microsoft Excel or Google Sheets) have built-in functions to calculate percentages quickly and accurately. Simply enter the fraction (60/65) or use the proportion method and let the calculator do the work.
Q: Are there other ways to express 60 out of 65 besides a percentage?
A: Yes, you can express it as a decimal (approximately 0.923) or as a simplified fraction (12/13). The choice of representation depends on the context and the desired level of precision.
Q: What if the numbers are much larger or smaller?
A: The same methods apply regardless of the magnitude of the numbers. The principles of forming a fraction, converting to a decimal, and then to a percentage remain the same.
Q: Why is understanding percentages important?
A: Percentages provide a standardized way to compare proportions, making it easier to understand and interpret data across different scales. This is crucial in various fields, from finance and science to everyday life.
Conclusion
Calculating 60 out of 65 as a percentage involves straightforward steps, regardless of the method employed. Understanding the underlying principles allows you to confidently tackle similar problems and apply percentage calculations to diverse situations. Whether using the fraction method, the direct proportion method, or technology, achieving an accurate and meaningful result requires careful attention to detail and an understanding of the implications of rounding. Remember that mastering percentages empowers you to analyze data effectively and make informed decisions in various aspects of your life. From academic achievements to financial planning, the skill of percentage calculation remains indispensable.
Latest Posts
Latest Posts
-
Convert Ac Voltage To Dc
Sep 20, 2025
-
1 10th Of A Meter
Sep 20, 2025
-
Bid Price And Ask Price
Sep 20, 2025
-
Potable And Nonpotable Water Definition
Sep 20, 2025
-
How Many Combinations 3 Numbers
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 60 65 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.