6 Divided By 1 4
candidatos
Sep 19, 2025 · 6 min read
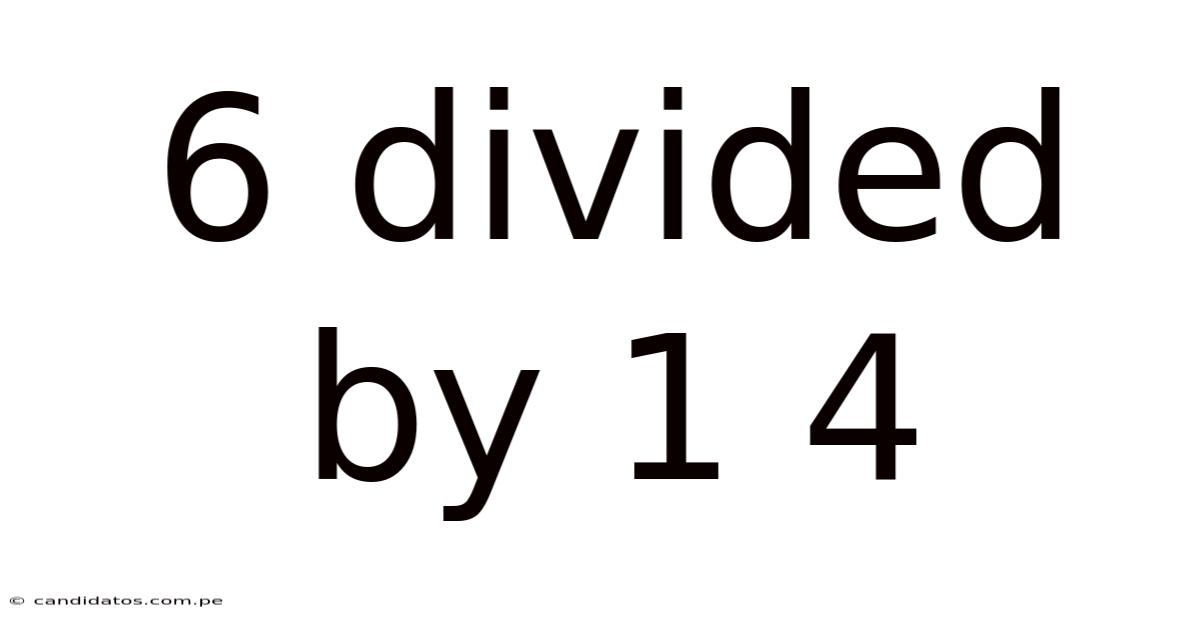
Table of Contents
Unpacking 6 Divided by 1 1/4: A Deep Dive into Fraction Division
This article explores the seemingly simple problem of 6 divided by 1 1/4, delving beyond the basic solution to uncover the underlying mathematical principles and practical applications. Understanding this seemingly straightforward calculation reveals crucial concepts in fraction manipulation and lays the groundwork for more complex mathematical operations. We'll cover the process step-by-step, explain the underlying rationale, and even look at real-world scenarios where this type of calculation is relevant.
Introduction: Why This Problem Matters
Dividing by mixed numbers (a whole number and a fraction, like 1 1/4) might seem intimidating, but mastering this skill is fundamental to a strong grasp of arithmetic. This seemingly simple problem—6 divided by 1 1/4—offers a perfect opportunity to practice key fraction manipulation techniques and build a deeper understanding of division itself. The ability to confidently solve problems like this is crucial for various fields, including cooking, construction, and even programming.
Method 1: Converting to Improper Fractions
The most common and generally preferred method for dividing fractions involves converting mixed numbers into improper fractions. An improper fraction has a numerator larger than or equal to its denominator.
Step 1: Convert the Mixed Number to an Improper Fraction:
The mixed number 1 1/4 can be converted to an improper fraction as follows:
- Multiply the whole number (1) by the denominator (4): 1 * 4 = 4
- Add the numerator (1): 4 + 1 = 5
- Keep the same denominator (4): The improper fraction is 5/4.
Step 2: Rewrite the Division Problem:
Our problem now becomes 6 ÷ 5/4.
Step 3: Remember the "Keep, Change, Flip" Rule:
Dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down.
- Keep: the first number (6). We can represent 6 as the fraction 6/1.
- Change: the division sign (÷) to a multiplication sign (×).
- Flip: the second fraction (5/4) to its reciprocal (4/5).
Step 4: Multiply the Fractions:
Now, multiply the numerators together and the denominators together:
(6/1) × (4/5) = (6 × 4) / (1 × 5) = 24/5
Step 5: Simplify to a Mixed Number (If Necessary):
The improper fraction 24/5 can be converted back to a mixed number:
- Divide the numerator (24) by the denominator (5): 24 ÷ 5 = 4 with a remainder of 4.
- The whole number is the quotient (4).
- The numerator of the fraction is the remainder (4).
- The denominator remains the same (5).
Therefore, 24/5 = 4 4/5.
Conclusion of Method 1: 6 divided by 1 1/4 equals 4 4/5.
Method 2: Using Decimal Conversion
Another approach involves converting both numbers into decimals before performing the division.
Step 1: Convert the Mixed Number to a Decimal:
1 1/4 is equal to 1.25 (because 1/4 is 0.25).
Step 2: Perform the Division:
Divide 6 by 1.25: 6 ÷ 1.25 = 4.8
Step 3: Convert the Decimal Back to a Fraction (if needed):
To convert 4.8 back to a fraction, we can write it as 48/10, which simplifies to 24/5. This, as we saw in Method 1, equals 4 4/5.
Conclusion of Method 2: Again, 6 divided by 1 1/4 equals 4 4/5. While this method might seem simpler for some, it's crucial to remember that the decimal representation might not always be exact for all fractions, potentially introducing rounding errors in more complex calculations.
The Underlying Mathematics: Why Does "Keep, Change, Flip" Work?
The "Keep, Change, Flip" rule isn't just a trick; it's a direct consequence of the definition of division and the properties of fractions. Division is essentially the inverse operation of multiplication. When we divide a by b (a ÷ b), we're asking "what number, when multiplied by b, equals a?"
Let's consider our problem: 6 ÷ (5/4). We're looking for a number x such that x × (5/4) = 6.
To solve for x, we can multiply both sides of the equation by the reciprocal of (5/4), which is (4/5):
x × (5/4) × (4/5) = 6 × (4/5)
The (5/4) and (4/5) cancel each other out, leaving:
x = 6 × (4/5) = 24/5 = 4 4/5
This demonstrates why the "Keep, Change, Flip" method works—it's a shortcut to solving the underlying equation.
Real-World Applications: Where This Matters
The ability to divide by mixed numbers isn't just an academic exercise; it has practical applications in various fields:
- Cooking and Baking: Scaling recipes up or down often requires dividing ingredients by mixed numbers. For example, if a recipe calls for 1 1/4 cups of flour and you want to make half the recipe, you'll need to calculate 1 1/4 ÷ 2.
- Construction and Carpentry: Measuring and cutting materials accurately often involves fractions and mixed numbers. Dividing lengths or quantities is essential for precise work.
- Sewing and Tailoring: Calculating fabric requirements and making adjustments to patterns often involves working with fractional measurements and mixed numbers.
- Finance and Budgeting: Dividing expenses or allocating resources might involve working with fractions and mixed numbers to represent percentages or proportions.
- Engineering and Design: Many engineering and design calculations involve precise measurements and proportions, requiring proficiency in fraction division.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to solve this problem?
A: Yes, most calculators can handle fraction division. However, understanding the underlying principles is crucial for problem-solving in more complex situations where a calculator might not be readily available or where you need to perform mental calculations.
Q: Is there another way to solve this problem?
A: While the methods outlined above are the most common and efficient, you could also use long division after converting everything to decimals. However, this method can be more prone to rounding errors.
Q: Why is it important to learn how to work with fractions?
A: Fractions represent parts of a whole, a fundamental concept in many areas of life and various academic disciplines. Proficiency with fractions is essential for higher-level mathematics and problem-solving.
Q: What if the numbers were larger or involved more complex fractions?
A: The same principles apply. Convert mixed numbers to improper fractions, apply the "Keep, Change, Flip" rule, and simplify the resulting fraction. The process might take longer, but the underlying concepts remain the same.
Conclusion: Mastering Fraction Division
Understanding how to divide by mixed numbers, such as solving 6 divided by 1 1/4, is a crucial skill in mathematics. The methods discussed—converting to improper fractions and using decimals—both lead to the same correct answer: 4 4/5. Mastering these techniques builds a strong foundation for more advanced mathematical concepts and equips you with practical skills applicable across various fields. Remember, the key is not just getting the right answer but also understanding the why behind the method. Practice these techniques regularly, and you’ll find that fraction division becomes second nature. The seemingly simple problem of 6 divided by 1 1/4 serves as a powerful gateway to a deeper appreciation of the elegance and practicality of mathematics.
Latest Posts
Latest Posts
-
13 Degrees C To F
Sep 19, 2025
-
Animal Name Starting From K
Sep 19, 2025
-
Angles In Parallel Lines Worksheet
Sep 19, 2025
-
3 By 2 Digit Multiplication
Sep 19, 2025
-
Words With The Or Sound
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 6 Divided By 1 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.