6 8 As A Percent
candidatos
Sep 24, 2025 · 5 min read
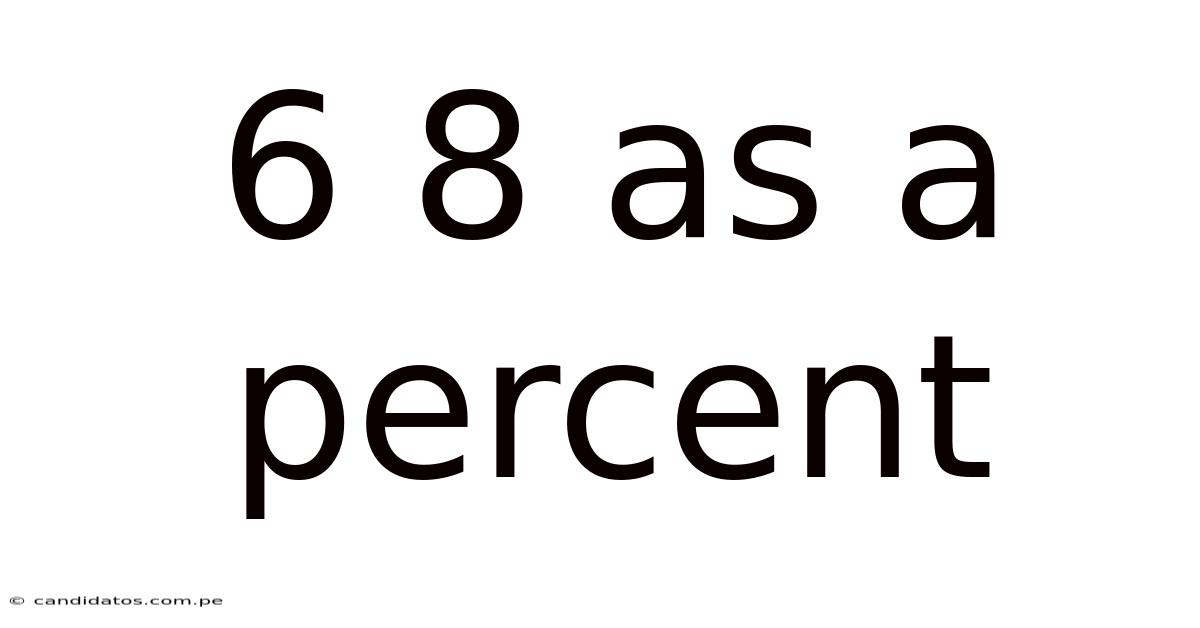
Table of Contents
Understanding 6/8 as a Percentage: A Comprehensive Guide
What is 6/8 as a percent? This seemingly simple question opens the door to a deeper understanding of fractions, decimals, and percentages – fundamental concepts in mathematics with wide-ranging applications in everyday life, from calculating discounts to understanding financial reports. This comprehensive guide will not only answer the initial question but also equip you with the tools and knowledge to confidently tackle similar percentage calculations. We'll explore the core concepts, provide step-by-step solutions, and delve into the underlying mathematical principles.
Understanding Fractions, Decimals, and Percentages
Before diving into the calculation, let's solidify our understanding of the three core components: fractions, decimals, and percentages. They are all different ways of representing parts of a whole.
-
Fractions: A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For example, in the fraction 6/8, 6 is the numerator and 8 is the denominator. This means 6 out of 8 equal parts.
-
Decimals: Decimals are another way to represent parts of a whole. They use a base-ten system, with digits to the right of the decimal point representing tenths, hundredths, thousandths, and so on. For instance, 0.5 represents half (5/10), and 0.75 represents three-quarters (75/100).
-
Percentages: Percentages represent parts of a whole as a fraction of 100. The symbol "%" represents "per cent," meaning "out of 100." So, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
The ability to convert between these three forms is crucial for various mathematical operations. Understanding their interrelationship is key to solving percentage problems effectively.
Converting 6/8 to a Percentage: Step-by-Step Guide
Now, let's tackle the main question: how do we convert the fraction 6/8 into a percentage? There are two primary methods:
Method 1: Simplifying the Fraction and then Converting
This method involves first simplifying the fraction to its lowest terms and then converting the simplified fraction to a decimal and finally to a percentage.
-
Simplify the Fraction: The fraction 6/8 can be simplified by finding the greatest common divisor (GCD) of 6 and 8, which is 2. Dividing both the numerator and the denominator by 2, we get:
6/8 = (6 ÷ 2) / (8 ÷ 2) = 3/4
-
Convert the Simplified Fraction to a Decimal: To convert the fraction 3/4 to a decimal, we divide the numerator (3) by the denominator (4):
3 ÷ 4 = 0.75
-
Convert the Decimal to a Percentage: To convert the decimal 0.75 to a percentage, we multiply it by 100 and add the percentage symbol (%):
0.75 × 100 = 75%
Therefore, 6/8 is equal to 75%.
Method 2: Direct Conversion from Fraction to Percentage
This method involves directly converting the fraction to a percentage without simplifying first.
-
Convert the Fraction to a Decimal: Divide the numerator (6) by the denominator (8):
6 ÷ 8 = 0.75
-
Convert the Decimal to a Percentage: Multiply the decimal by 100 and add the percentage symbol (%):
0.75 × 100 = 75%
This method yields the same result: 6/8 is equal to 75%.
Illustrative Examples: Real-World Applications
Understanding percentage calculations is vital in various real-world scenarios. Let's explore a few examples to solidify our understanding:
Example 1: Test Scores
Imagine a student scores 6 out of 8 questions correctly on a quiz. To determine their percentage score, we would use the same method:
6/8 = 0.75 = 75%
The student achieved a 75% score on the quiz.
Example 2: Sales Discounts
A store offers a 6/8 discount on selected items. This means a discount of 75% (as 6/8 simplifies to 3/4 or 75%). If an item is priced at $100, the discount would be:
$100 × 0.75 = $75
The discounted price would be $100 - $75 = $25.
Example 3: Completion Rate
A project has 8 tasks, and 6 of them are completed. The completion rate is:
6/8 = 0.75 = 75%
The project is 75% complete.
Further Exploration: Percentage Increase and Decrease
The concept of percentages extends beyond simply representing parts of a whole. We often use percentages to describe increases or decreases in quantities.
For instance, if a quantity increases from 8 to 10, the percentage increase is calculated as follows:
- Find the difference: 10 - 8 = 2
- Divide the difference by the original quantity: 2/8 = 0.25
- Multiply by 100 to express as a percentage: 0.25 × 100 = 25%
Therefore, the quantity increased by 25%. Similar calculations can be applied to determine percentage decreases.
Frequently Asked Questions (FAQs)
Q1: What if the fraction is not easily simplified?
A1: Even if a fraction isn't easily simplified, you can still use the direct conversion method (Method 2) to convert it to a percentage. Simply divide the numerator by the denominator and then multiply the result by 100.
Q2: Can I use a calculator to convert fractions to percentages?
A2: Absolutely! Most calculators have the capability to perform division and multiplication, making the conversion process quick and easy.
Q3: Why is understanding percentages important?
A3: Percentages are a fundamental tool for understanding proportions, comparing quantities, and expressing data in a clear and concise manner. They are widely used in various fields, including finance, statistics, science, and everyday life.
Q4: Are there any online tools to help with percentage calculations?
A4: While this article doesn't endorse external links, many websites and apps offer free online percentage calculators that can simplify the conversion process.
Conclusion
Converting 6/8 to a percentage demonstrates the interconnectedness of fractions, decimals, and percentages. Understanding these relationships is crucial for solving various mathematical problems and interpreting data in a meaningful way. By mastering these fundamental concepts, you'll be well-equipped to tackle more complex percentage calculations in various real-world applications. Remember, practice is key to improving your proficiency. Work through different examples, and soon you'll be confidently converting fractions to percentages and vice versa. The ability to understand and manipulate percentages is a valuable skill that will benefit you in many aspects of life.
Latest Posts
Latest Posts
-
Sodium Hydroxide And Nitric Acid
Sep 24, 2025
-
Lead 2 Nitrate Chemical Formula
Sep 24, 2025
-
Five Letter Words Ending El
Sep 24, 2025
-
16 30 As A Percent
Sep 24, 2025
-
Subtract Fraction With Different Denominators
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 6 8 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.