6 23 As A Percentage
candidatos
Sep 18, 2025 · 5 min read
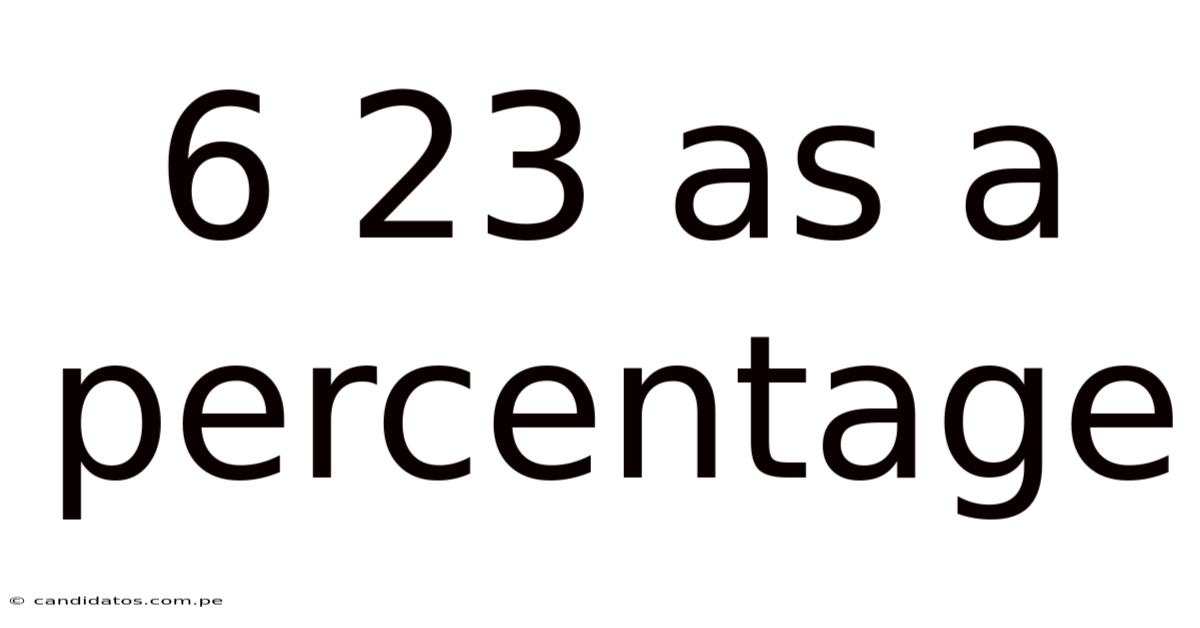
Table of Contents
Understanding 6/23 as a Percentage: A Comprehensive Guide
Understanding how to convert fractions to percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and sales tax to understanding statistical data and financial reports. This comprehensive guide will delve into the process of converting the fraction 6/23 into a percentage, exploring the underlying concepts and offering practical examples along the way. We will cover not just the calculation itself, but also the broader context of percentage calculations and their significance.
Introduction to Fractions, Decimals, and Percentages
Before we dive into converting 6/23, let's refresh our understanding of the relationship between fractions, decimals, and percentages. They are all different ways of representing parts of a whole.
-
Fractions: Represent a part of a whole using a numerator (the top number) and a denominator (the bottom number). For example, 6/23 means 6 out of 23 equal parts.
-
Decimals: Represent a part of a whole using base-10 notation. They are essentially fractions where the denominator is a power of 10 (10, 100, 1000, etc.). For example, 0.5 is equivalent to ½, and 0.25 is equivalent to ¼.
-
Percentages: Represent a part of a whole as a fraction of 100. The symbol "%" represents "per hundred". For example, 50% means 50 out of 100, or ½.
Converting between these three forms is crucial for various mathematical operations. Understanding their interconnectedness is key to mastering this skill.
Converting 6/23 to a Percentage: The Step-by-Step Process
The process of converting a fraction like 6/23 to a percentage involves two main steps:
Step 1: Convert the Fraction to a Decimal
To convert a fraction to a decimal, we simply divide the numerator by the denominator. In this case:
6 ÷ 23 ≈ 0.260869565
We use the approximation symbol (≈) because the decimal representation of 6/23 is non-terminating (it goes on infinitely without repeating). We'll round this to a suitable number of decimal places later, depending on the required level of accuracy.
Step 2: Convert the Decimal to a Percentage
To convert a decimal to a percentage, we multiply the decimal by 100 and add the "%" symbol. So, for our decimal 0.260869565:
0.260869565 × 100 ≈ 26.0869565%
Step 3: Rounding for Practical Use
The percentage we obtained, 26.0869565%, is quite precise but might be cumbersome to use in many practical situations. The level of rounding depends on the context. Here are some examples:
- Rounding to the nearest whole number: 26%
- Rounding to one decimal place: 26.1%
- Rounding to two decimal places: 26.09%
The choice of rounding depends on the context and the desired level of accuracy. For most everyday purposes, rounding to one or two decimal places is sufficient.
The Importance of Understanding Percentage Calculations
Understanding how to convert fractions to percentages is not merely an academic exercise. It's a crucial skill applicable across various real-world scenarios:
-
Financial Calculations: Calculating interest rates, discounts, sales tax, profit margins, and investment returns all involve percentage calculations. Understanding these calculations empowers you to make informed financial decisions.
-
Statistical Analysis: Percentages are frequently used to represent data and proportions in various statistical analyses. Understanding percentages is crucial for interpreting charts, graphs, and statistical reports.
-
Everyday Life: Calculating tips in restaurants, understanding sales discounts, and interpreting survey results all rely on the ability to work with percentages.
-
Scientific Applications: Percentages are used extensively in scientific fields like chemistry (concentration of solutions), biology (population growth rates), and physics (efficiency of machines).
Beyond the Basic Calculation: Deeper Understanding of Ratios and Proportions
The conversion of 6/23 to a percentage highlights the fundamental relationship between ratios and proportions. The fraction 6/23 represents a ratio of 6 to 23. When we convert this ratio to a percentage, we are expressing it as a proportion out of 100. This concept extends to numerous other applications in mathematics and various fields.
Advanced Concepts and Applications
While converting 6/23 to a percentage is a relatively simple calculation, the underlying principles can be applied to more complex scenarios. For example:
-
Calculating percentage increase or decrease: This involves finding the percentage change between two values. It's used extensively in tracking economic indicators, sales growth, and population changes.
-
Percentage points: These represent the absolute difference between two percentages, not a percentage change. Understanding the difference between percentage points and percentage change is vital for accurate interpretation of data.
-
Compound interest: This involves calculating interest on both the principal amount and accumulated interest. It's a crucial concept in finance and investment.
Frequently Asked Questions (FAQ)
Q: Why is the decimal representation of 6/23 non-terminating?
A: A decimal representation is non-terminating if the division process doesn't end with a remainder of zero. This often occurs when the denominator of the fraction has prime factors other than 2 and 5. The denominator 23 is a prime number, leading to a non-terminating decimal.
Q: What is the difference between a percentage and a percentage point?
A: A percentage point represents the absolute difference between two percentages, while a percentage change represents the relative change. For example, if something increases from 10% to 15%, the increase is 5 percentage points, but the percentage increase is 50% (5/10 x 100%).
Q: How can I perform these calculations without a calculator?
A: For simpler fractions, you can sometimes simplify them before converting to a decimal. However, for fractions like 6/23, manual calculation is tedious. A calculator or spreadsheet software significantly simplifies the process.
Conclusion
Converting 6/23 to a percentage (approximately 26.09%) is a straightforward process involving converting the fraction to a decimal and then multiplying by 100. However, understanding the underlying concepts of fractions, decimals, percentages, ratios, and proportions is crucial for applying these skills effectively in diverse contexts. This knowledge empowers you to make informed decisions in finance, statistics, and everyday life, showcasing the practical relevance and importance of seemingly simple mathematical concepts. Remember that accuracy and appropriate rounding are essential when applying percentage calculations in real-world scenarios.
Latest Posts
Latest Posts
-
6 Times Table Practice Worksheet
Sep 18, 2025
-
2020 English Standard Paper 1
Sep 18, 2025
-
Difference Between Usb 2 0 3 0
Sep 18, 2025
-
Convert Kw To Kva Calculator
Sep 18, 2025
-
5 Letter Word Starting Sy
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 6 23 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.