52 75 As A Percentage
candidatos
Sep 23, 2025 · 5 min read
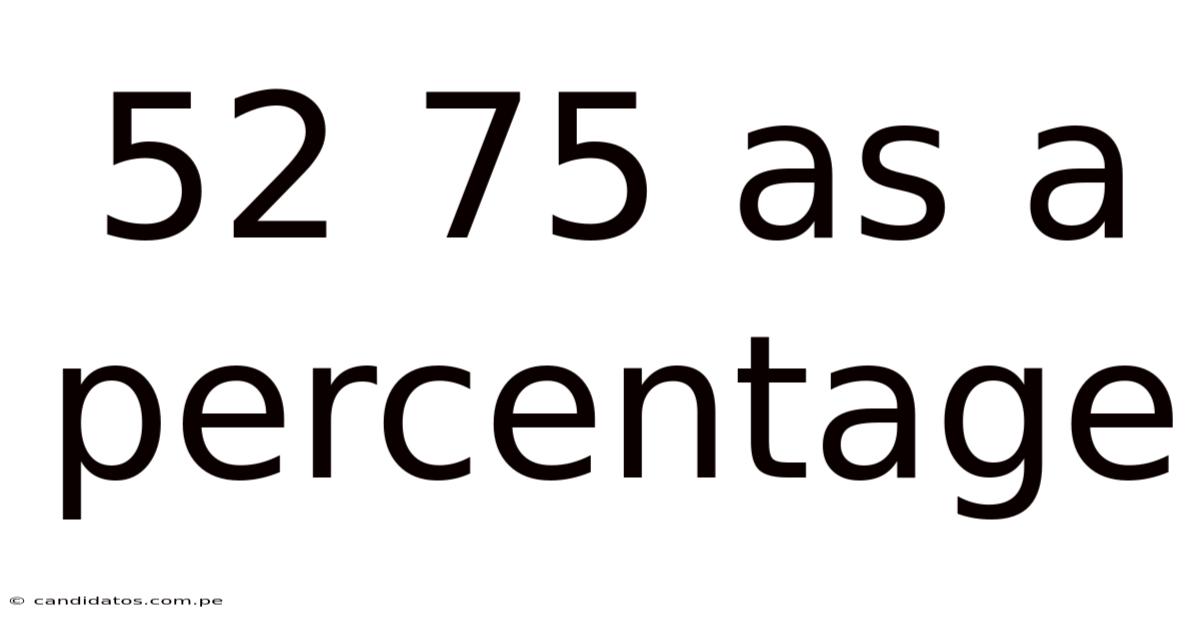
Table of Contents
Decoding 52/75 as a Percentage: A Comprehensive Guide
Understanding percentages is a fundamental skill in various aspects of life, from calculating discounts in a store to analyzing data in a professional setting. This article provides a comprehensive explanation of how to convert the fraction 52/75 into a percentage, exploring different methods and delving into the underlying mathematical principles. We’ll also tackle common misconceptions and address frequently asked questions. This guide aims to equip you with the confidence and knowledge to tackle similar percentage calculations independently.
Understanding Percentages and Fractions
Before we dive into converting 52/75, let's establish a clear understanding of percentages and their relationship with fractions. A percentage is simply a fraction expressed as a part of 100. The symbol "%" signifies "per hundred" or "out of 100". For instance, 50% means 50 out of 100, which can also be written as the fraction 50/100 or the decimal 0.5.
Fractions, on the other hand, represent parts of a whole. They are expressed as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). The fraction 52/75 indicates that we have 52 parts out of a total of 75 parts. To convert a fraction to a percentage, we need to find the equivalent fraction with a denominator of 100.
Method 1: Direct Conversion using a Calculator
The simplest method to convert 52/75 to a percentage is using a calculator. Simply divide the numerator (52) by the denominator (75) and multiply the result by 100.
- Step 1: Division: 52 ÷ 75 = 0.693333...
- Step 2: Multiplication: 0.693333... × 100 = 69.3333...%
Therefore, 52/75 is approximately 69.33%. The repeating decimal indicates that the percentage is an approximation. For most practical purposes, rounding to two decimal places (69.33%) is sufficient.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
This method provides a deeper understanding of the underlying mathematical process. The goal is to manipulate the fraction 52/75 to create an equivalent fraction where the denominator is 100. This can be achieved by finding a number that, when multiplied by 75, results in 100. However, there is no whole number that satisfies this condition. This means we need to use a slightly different approach. We will instead calculate the decimal equivalent and then convert that decimal to a percentage.
- Step 1: Decimal Conversion: Divide 52 by 75: 52 ÷ 75 ≈ 0.6933
- Step 2: Percentage Conversion: Multiply the decimal by 100: 0.6933 × 100 = 69.33%
Method 3: Proportion Method
The proportion method is another useful approach. We set up a proportion where x represents the percentage we are trying to find:
52/75 = x/100
To solve for x, we cross-multiply:
75x = 5200
Then, we divide both sides by 75:
x = 5200 ÷ 75 ≈ 69.33
Therefore, 52/75 is approximately 69.33%.
Understanding the Significance of the Decimal
The decimal value obtained in the calculations (approximately 0.6933) represents the fraction as a part of one. This is a crucial concept because it shows that 52/75 is equivalent to approximately 0.6933 of a whole. Multiplying this decimal by 100 simply scales the value to represent it as a percentage, which is inherently a fraction out of 100.
Rounding and Accuracy
When dealing with percentages, rounding is often necessary to express the value concisely. The level of rounding depends on the context and the required accuracy. In many scenarios, rounding to two decimal places (69.33%) is sufficient. However, if higher precision is needed, you may retain more decimal places or use the fraction form directly if the application allows for it. It is crucial to understand that rounding introduces a slight error. In some cases, especially when dealing with financial calculations, maintaining a higher degree of accuracy might be crucial.
Practical Applications of Percentage Conversions
Converting fractions to percentages is valuable in various fields:
- Business and Finance: Calculating profit margins, discounts, interest rates, and tax rates.
- Science and Statistics: Representing data in charts and graphs, interpreting survey results, and analyzing experimental outcomes.
- Everyday Life: Understanding sales discounts, calculating tips, and comprehending information presented in percentages.
Frequently Asked Questions (FAQ)
Q: Can I use a different method to calculate the percentage?
A: Yes, you can use any method that involves dividing the numerator by the denominator and then multiplying the result by 100. The choice of method depends on personal preference and the tools available.
Q: What if the decimal value is very long?
A: If the decimal value has many repeating digits, you can round it to a reasonable number of decimal places. The appropriate number of decimal places depends on the level of accuracy required for the specific application.
Q: Is it always necessary to round the percentage?
A: While rounding simplifies the representation, it isn't always necessary. If the application requires high precision, retaining the full decimal value is preferable.
Q: Why is understanding percentages important?
A: Percentages provide a standardized way to compare proportions and fractions. This makes it easier to understand and interpret data across different contexts. They are frequently used in everyday life and essential for various professional fields.
Q: What are some common mistakes to avoid when calculating percentages?
A: Common mistakes include misplacing the decimal point, using the wrong order of operations (dividing before multiplying), and neglecting to multiply by 100. Carefully following the steps outlined in any chosen method is crucial to accurate results.
Conclusion
Converting 52/75 to a percentage involves a straightforward process, whether you use a calculator, find an equivalent fraction, or employ the proportion method. The result is approximately 69.33%. Understanding the various methods and their underlying principles allows for a deeper grasp of percentages and their applications in various contexts. Remember to always consider the required level of accuracy when rounding and to carefully execute the steps of chosen methods to prevent errors. By mastering these techniques, you'll build a stronger foundation in mathematical concepts that are essential across many disciplines.
Latest Posts
Latest Posts
-
Is Ammonium Acidic Or Basic
Sep 23, 2025
-
How Long Is 10 Kilometers
Sep 23, 2025
-
X 2 X 4 1
Sep 23, 2025
-
List Of Spices From India
Sep 23, 2025
-
Colour That Starts With I
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 52 75 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.