5 X 47 X 20
candidatos
Sep 20, 2025 · 6 min read
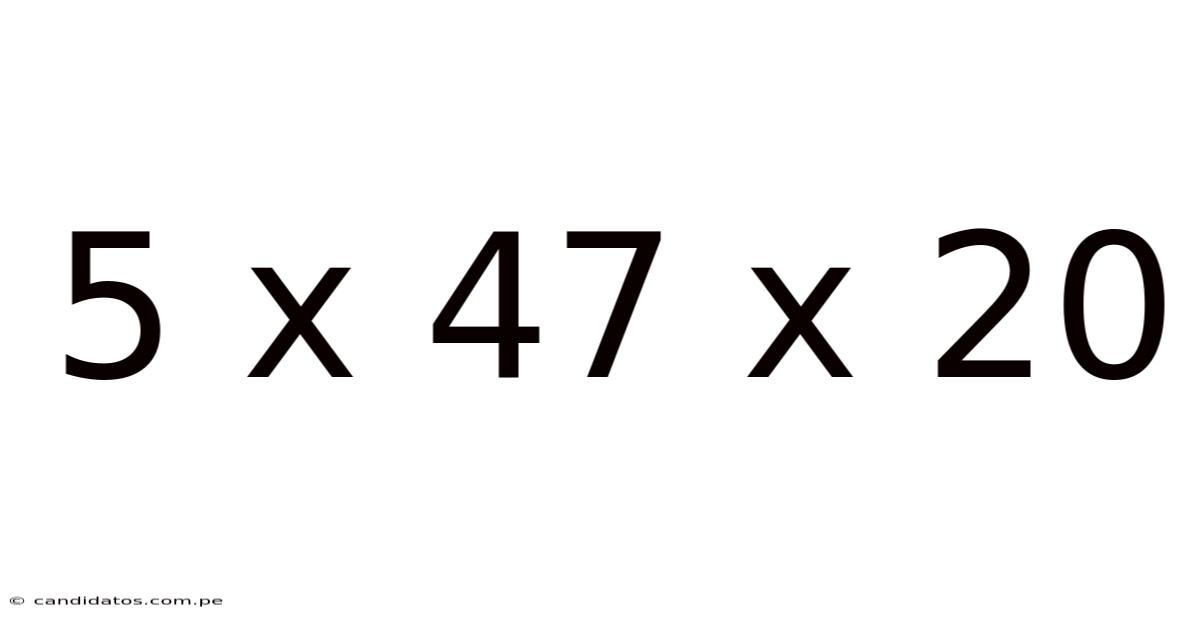
Table of Contents
Decoding 5 x 47 x 20: A Deep Dive into Multiplication and its Applications
This article explores the seemingly simple calculation of 5 x 47 x 20, delving beyond the immediate answer to uncover the underlying mathematical principles and its broader applications in various fields. Understanding this seemingly basic equation offers a gateway to appreciating more complex mathematical concepts and their real-world relevance. We'll examine different approaches to solving the problem, explore the properties of multiplication, and discuss how this type of calculation is used in everyday life and advanced mathematical disciplines.
Introduction: More Than Just Numbers
At first glance, 5 x 47 x 20 appears to be a straightforward multiplication problem. The answer, easily obtained with a calculator, is 4700. However, dissecting this equation reveals a wealth of mathematical concepts and practical applications. This seemingly simple calculation provides a foundation for understanding fundamental mathematical operations, number properties, and their relevance in various fields like engineering, finance, and computer science. This article will guide you through different methods of solving this problem, explain the underlying principles, and highlight the significance of this seemingly simple calculation in a broader context.
Method 1: Direct Multiplication
The most straightforward approach is to perform the multiplication sequentially. We can begin by multiplying 5 and 47:
5 x 47 = 235
Then, multiply the result by 20:
235 x 20 = 4700
This method, while simple, demonstrates the associative property of multiplication, which states that the order in which we multiply numbers doesn't change the result. (5 x 47) x 20 = 5 x (47 x 20).
Method 2: Rearranging for Efficiency
Multiplication allows for rearranging the numbers to simplify the calculation. Notice that we have 5 and 20, which are easily multiplied together:
5 x 20 = 100
Now the problem becomes:
100 x 47 = 4700
This method demonstrates the commutative and associative properties of multiplication, making the calculation considerably easier. This approach highlights the importance of recognizing opportunities for simplification within mathematical problems.
Method 3: Distributive Property
While less efficient in this specific instance, understanding the distributive property is crucial for more complex calculations. The distributive property states that a(b + c) = ab + ac. We can rewrite 47 as (50 - 3) and then apply the distributive property:
5 x 20 x (50 - 3) = 100 x (50 - 3) = (100 x 50) - (100 x 3) = 5000 - 300 = 4700
This method illustrates a different approach to solving the problem and strengthens the understanding of fundamental algebraic concepts.
The Significance of the Commutative and Associative Properties
The ease with which we can rearrange the numbers in 5 x 47 x 20 emphasizes the importance of the commutative and associative properties of multiplication. The commutative property states that the order of the numbers does not affect the product (a x b = b x a). The associative property states that the grouping of numbers does not affect the product ((a x b) x c = a x (b x c)). These properties are fundamental to arithmetic and algebra, enabling us to simplify complex calculations and solve equations more efficiently. They are also critical in more advanced mathematical concepts like matrix multiplication and abstract algebra.
Applications in Real-World Scenarios
This seemingly simple equation, 5 x 47 x 20, mirrors various real-world scenarios:
- Calculating Costs: Imagine buying 20 boxes of pens, each containing 5 packs with 47 pens each. The total number of pens would be 5 x 47 x 20 = 4700.
- Area Calculation: Consider a rectangular field with dimensions 47 meters by 20 meters. If you need to calculate the area of 5 such fields, the calculation would again be 5 x 47 x 20 = 4700 square meters.
- Inventory Management: A warehouse might store 20 pallets, each holding 5 crates, with 47 items in each crate. The total number of items is 4700.
- Scaling Production: A factory producing 47 units per batch, running 5 batches a day for 20 days, produces 4700 units.
These examples demonstrate how the multiplication of three numbers is integral to various aspects of everyday life and business.
Expanding the Concept: Beyond Basic Multiplication
Understanding 5 x 47 x 20 provides a springboard for exploring more advanced mathematical concepts.
- Powers and Exponents: This equation can be easily adapted to incorporate exponents. For example, we could consider (5 x 47)² x 20, which introduces the concept of squaring a number and its impact on the overall result.
- Algebraic Equations: The equation could be part of a larger algebraic equation, introducing variables and unknowns. This would necessitate employing algebraic manipulation techniques to solve for unknown values.
- Calculus and Differential Equations: While seemingly distant, understanding the basics of multiplication is foundational for grasping more complex mathematical concepts like limits, derivatives, and integrals, which are crucial in calculus and differential equations.
Frequently Asked Questions (FAQ)
Q: What are the prime factors of 4700?
A: To find the prime factors of 4700, we can start by factoring out the obvious factors: 4700 = 100 x 47 = (2 x 5)² x 47. Therefore, the prime factorization of 4700 is 2² x 5² x 47.
Q: Can this calculation be done using different number bases?
A: Yes, absolutely. This calculation can be performed using different number bases, such as binary, octal, or hexadecimal. However, the fundamental principles of multiplication remain the same, regardless of the number base used. The result, however, would be represented differently depending on the chosen base.
Q: Are there other efficient methods to multiply large numbers?
A: Yes, various algorithms exist for multiplying large numbers more efficiently than the standard method. These include the Karatsuba algorithm, Toom-Cook multiplication, and the Fast Fourier Transform (FFT)-based multiplication. These algorithms are particularly useful when dealing with extremely large numbers where computational efficiency becomes critical.
Q: How does this relate to computer programming?
A: Multiplication is a fundamental arithmetic operation in computer programming. Understanding its properties and efficient implementation is essential in writing optimized code for various applications, including graphics processing, scientific computing, and simulations.
Conclusion: The Unsung Importance of Simplicity
The seemingly simple calculation of 5 x 47 x 20 serves as a powerful illustration of the fundamental principles of multiplication and their wide-ranging applications. While the answer itself is easily obtained, the journey of exploring different solution methods and uncovering the underlying mathematical properties reveals the depth and interconnectedness of mathematical concepts. From basic arithmetic to advanced mathematical disciplines and real-world applications, this simple equation demonstrates the unsung importance of seemingly straightforward calculations and their essential role in our understanding of the world around us. It encourages us to look beyond the immediate answer and appreciate the foundational knowledge underpinning even the simplest of mathematical operations. Mastering these fundamentals is key to unlocking a deeper appreciation for the power and elegance of mathematics.
Latest Posts
Latest Posts
-
Symbol For A Circuit Breaker
Sep 21, 2025
-
Important Crossword Clue 11 Letters
Sep 21, 2025
-
Carpet Cost Per Square Metre
Sep 21, 2025
-
Words That Start With Ki
Sep 21, 2025
-
Chile Peso To Canadian Dollar
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 5 X 47 X 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.