5 Percent Of 30 000
candidatos
Sep 19, 2025 · 5 min read
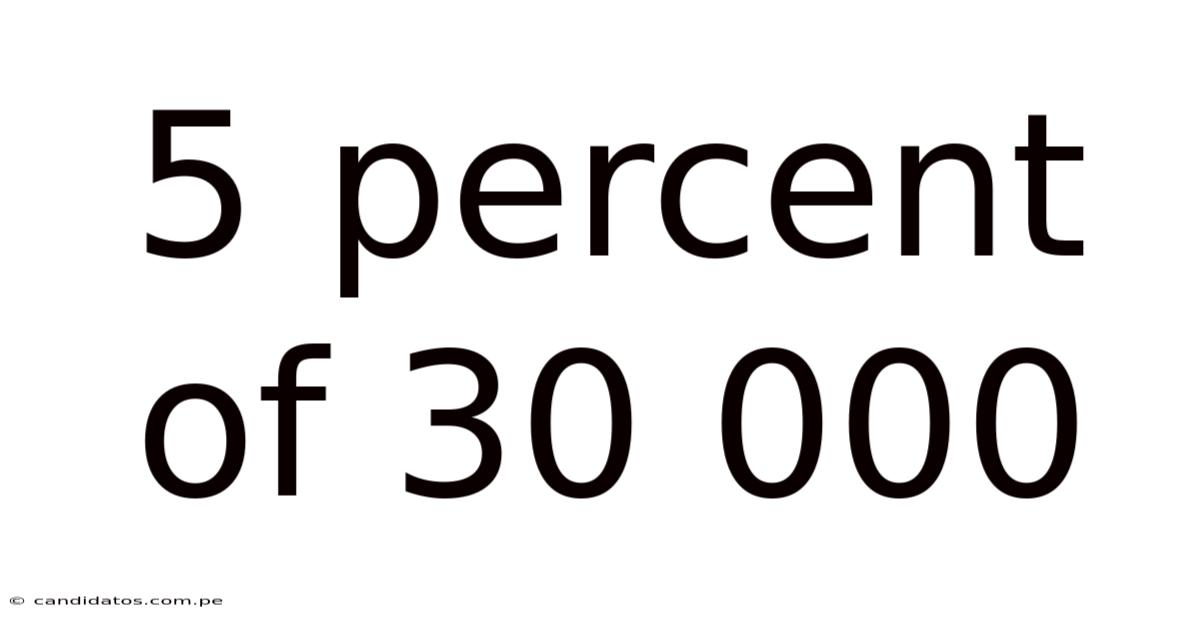
Table of Contents
Decoding 5 Percent of 30,000: A Deep Dive into Percentages and Their Applications
Calculating percentages is a fundamental skill applicable across numerous fields, from everyday budgeting to complex financial modeling. This article will meticulously explore the calculation of 5% of 30,000, explaining the process step-by-step, providing practical examples, and delving into the underlying mathematical principles. Understanding this seemingly simple calculation unlocks a broader understanding of percentage applications in various real-world scenarios. We'll also address frequently asked questions and explore alternative calculation methods.
Understanding Percentages: A Foundation
Before diving into the specific calculation, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent," meaning "out of one hundred." Therefore, 5% can be expressed as 5/100 or 0.05 as a decimal.
This understanding is crucial because it forms the basis of all percentage calculations. To find a percentage of a number, we multiply the number by the percentage expressed as a decimal.
Calculating 5% of 30,000: The Step-by-Step Process
Calculating 5% of 30,000 involves a straightforward process:
-
Convert the percentage to a decimal: As mentioned above, 5% is equivalent to 0.05.
-
Multiply the number by the decimal: Multiply 30,000 by 0.05: 30,000 x 0.05 = 1500
Therefore, 5% of 30,000 is 1500.
Practical Applications: Where Percentages Matter
The calculation of percentages, particularly finding a percentage of a larger number, has widespread practical applications. Let's explore some examples:
-
Sales and Discounts: Imagine a store offering a 5% discount on a $30,000 vehicle. Using our calculation, the discount amount would be $1500, making the final price $28,500. This is a common scenario in retail, where understanding percentages is essential for consumers and businesses alike.
-
Taxes and Fees: Government taxes and service fees are often expressed as percentages. For example, a 5% sales tax on a $30,000 purchase would add $1500 to the total cost. Understanding these percentages is crucial for budgeting and financial planning.
-
Commissions and Bonuses: Sales commissions and employee bonuses are frequently calculated as a percentage of sales or performance targets. If a salesperson earns a 5% commission on $30,000 worth of sales, their commission would be $1500.
-
Financial Investments: Percentage calculations are essential in finance. For instance, calculating investment returns, interest earned, or assessing the growth or decline of an investment portfolio often relies heavily on percentage calculations. A 5% annual return on a $30,000 investment would yield $1500 in profit.
-
Statistics and Data Analysis: Percentages are frequently used to represent proportions in data analysis. For example, if 5% of a sample of 30,000 people responded to a survey, that would represent 1500 respondents.
These examples highlight the versatility of percentage calculations. Mastering this fundamental mathematical concept is crucial for navigating various aspects of personal and professional life.
Alternative Calculation Methods
While the direct multiplication method is the most straightforward, alternative approaches can help enhance understanding and provide flexibility.
-
Using Fractions: We can express 5% as the fraction 5/100. Then, the calculation becomes (5/100) * 30,000. This simplifies to (1/20) * 30,000, which equals 1500. This method is particularly useful when dealing with simpler percentages or when mental calculation is preferred.
-
Breaking Down the Calculation: We can break down the calculation into smaller, more manageable steps. For instance, finding 1% of 30,000 is 300. Since 5% is five times 1%, we simply multiply 300 by 5 to get 1500. This method is beneficial for mental calculation and helps to build an intuitive understanding of percentage relationships.
-
Using a Calculator or Spreadsheet Software: For larger or more complex percentage calculations, using a calculator or spreadsheet software like Microsoft Excel or Google Sheets can significantly expedite the process and reduce the risk of errors. These tools often include built-in functions for percentage calculations.
Further Exploring Percentages: Advanced Concepts
While this article focuses on a specific percentage calculation, understanding the broader concept of percentages opens doors to more advanced mathematical applications.
-
Percentage Increase and Decrease: Calculating percentage changes is crucial in various contexts, including tracking economic growth, monitoring population changes, or assessing the performance of investments.
-
Compound Interest: Understanding compound interest involves calculating percentages repeatedly over time, showcasing the power of exponential growth.
-
Percentage Points: It’s crucial to differentiate between percentage change and percentage points. A change from 10% to 15% is a 5 percentage point increase, but a 50% increase in the percentage itself.
Frequently Asked Questions (FAQ)
Q: What if I need to calculate a different percentage of 30,000?
A: The same principle applies. Simply convert the desired percentage to a decimal and multiply it by 30,000. For example, to find 12% of 30,000, you would multiply 30,000 by 0.12, resulting in 3600.
Q: How can I calculate the percentage one number represents of another?
A: To find what percentage one number represents of another, divide the smaller number by the larger number and multiply the result by 100. For instance, to find what percentage 1500 is of 30,000, you would calculate (1500/30,000) * 100 = 5%.
Q: Are there any online tools to help with percentage calculations?
A: Numerous online calculators and websites are available to assist with percentage calculations. These tools can be particularly helpful for complex calculations or when dealing with large datasets.
Q: Why is understanding percentages important?
A: Understanding percentages is essential for everyday life, from budgeting and shopping to financial planning and career advancement. It’s a fundamental skill applied across various disciplines and industries.
Conclusion
Calculating 5% of 30,000, resulting in 1500, is a straightforward yet pivotal calculation demonstrating the core principles of percentage computations. This seemingly simple calculation opens doors to a wider understanding of percentages and their wide-ranging applications across diverse fields. By mastering this fundamental skill, individuals gain a valuable tool for navigating various personal and professional challenges, enhancing their problem-solving capabilities and decision-making processes. From financial management to data analysis, the ability to calculate percentages effectively is an invaluable asset. Remember to practice regularly and explore different approaches to solidify your understanding.
Latest Posts
Latest Posts
-
Words With Ax And Z
Sep 19, 2025
-
Words With X 3 Letter
Sep 19, 2025
-
Criminal Lawyer Vs Civil Lawyer
Sep 19, 2025
-
Beginning Sentences With Prepositional Phrases
Sep 19, 2025
-
Things To Do In Sines
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 5 Percent Of 30 000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.