5 75 As A Percent
candidatos
Sep 19, 2025 · 5 min read
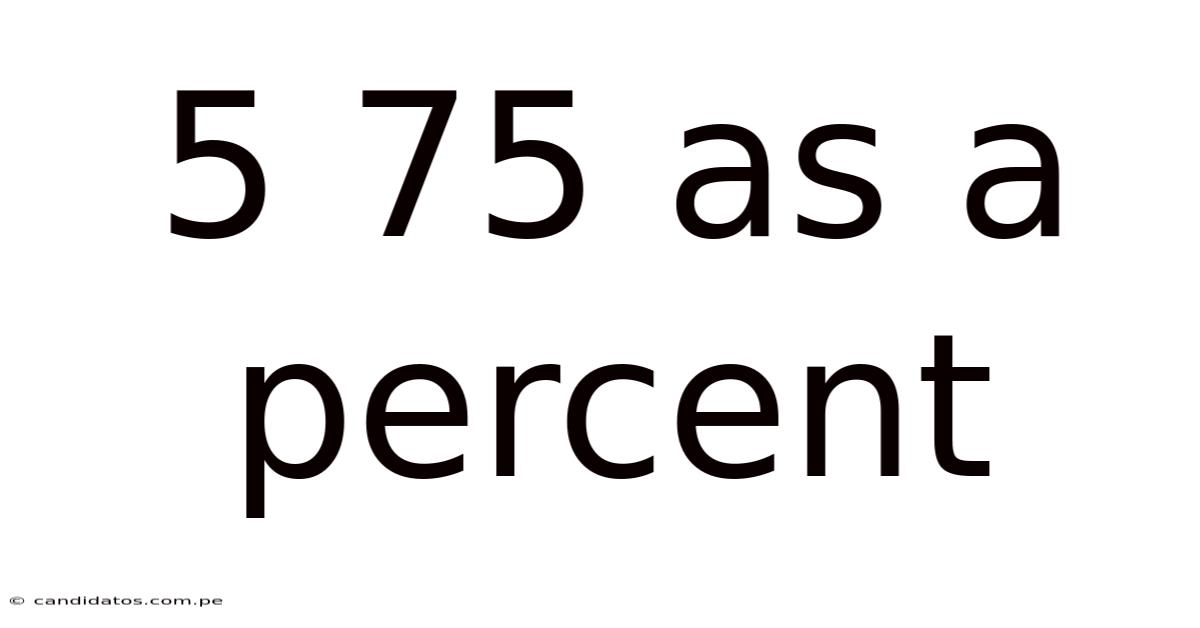
Table of Contents
5/75 as a Percent: A Comprehensive Guide to Fraction-to-Percentage Conversion
Understanding how to convert fractions to percentages is a fundamental skill in mathematics, applicable across various fields from everyday budgeting to advanced scientific calculations. This comprehensive guide will delve into the process of converting the fraction 5/75 into a percentage, explaining the underlying concepts in detail and offering practical examples. We'll explore different methods, address common misconceptions, and even delve into the broader context of fraction-to-percentage conversions. By the end, you'll not only know the answer to "What is 5/75 as a percent?" but also possess a solid understanding of the underlying principles.
Understanding Fractions and Percentages
Before jumping into the conversion, let's clarify the core concepts. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts you have, and the denominator indicates how many parts make up the whole. In our case, 5/75 means we have 5 parts out of a total of 75 parts.
A percentage, on the other hand, expresses a fraction as a portion of 100. The symbol "%" represents "per hundred" or "out of 100." Percentages are commonly used to represent proportions, rates, and changes. For example, 25% means 25 out of 100, which is equivalent to the fraction 25/100 or 1/4.
Method 1: Simplifying the Fraction
The most straightforward method involves simplifying the fraction before converting it to a percentage. This involves finding the greatest common divisor (GCD) of the numerator and the denominator and dividing both by it.
-
Find the GCD: The GCD of 5 and 75 is 5.
-
Simplify the Fraction: Divide both the numerator and denominator by the GCD: 5 ÷ 5 = 1 and 75 ÷ 5 = 15. This simplifies the fraction to 1/15.
-
Convert to a Decimal: Divide the numerator (1) by the denominator (15): 1 ÷ 15 ≈ 0.066666...
-
Convert to a Percentage: Multiply the decimal by 100: 0.066666... × 100 ≈ 6.67%.
Therefore, 5/75 simplifies to approximately 6.67%. The recurring decimal emphasizes the importance of rounding to an appropriate number of decimal places for practical applications. In most cases, rounding to two decimal places (6.67%) is sufficient.
Method 2: Direct Conversion to Percentage
This method skips the simplification step and directly converts the fraction to a percentage.
-
Convert to a Decimal: Divide the numerator (5) by the denominator (75): 5 ÷ 75 ≈ 0.066666...
-
Convert to a Percentage: Multiply the decimal by 100: 0.066666... × 100 ≈ 6.67%.
This method yields the same result as Method 1, demonstrating that simplification is not always necessary, though it can often simplify the calculations.
Method 3: Using Proportions
This method utilizes the concept of proportions to solve the problem. We know that a percentage is a fraction out of 100. We can set up a proportion to find the equivalent percentage:
5/75 = x/100
To solve for x (the percentage), we can cross-multiply:
75x = 500
x = 500/75
x ≈ 6.67
Therefore, 5/75 is approximately 6.67%.
Understanding the Decimal Representation
The recurring decimal 0.066666... in the previous calculations is a significant point. It represents a rational number, meaning it can be expressed as a fraction (1/15). However, its decimal representation is non-terminating, meaning it continues infinitely. Rounding is essential for practical use, and the level of precision required depends on the context.
Practical Applications of Percentage Conversions
The ability to convert fractions to percentages has numerous real-world applications:
- Financial Calculations: Determining interest rates, discounts, profit margins, and tax rates all involve percentage conversions.
- Statistics and Data Analysis: Representing data proportions, analyzing survey results, and calculating probabilities frequently involve percentages.
- Science and Engineering: Many scientific and engineering calculations require expressing ratios and proportions as percentages.
- Everyday Life: Understanding discounts in stores, calculating tips in restaurants, and comprehending statistics in news reports all depend on an understanding of percentages.
Frequently Asked Questions (FAQs)
Q: Why is it important to simplify fractions before converting them to percentages?
A: Simplifying fractions makes the calculation easier and reduces the chance of errors, especially with larger numbers. A simplified fraction often leads to a terminating decimal, making the conversion to a percentage more straightforward.
Q: What if I get a repeating decimal when converting a fraction to a percentage?
A: Repeating decimals are common when converting fractions. You should round the decimal to an appropriate number of decimal places based on the required level of accuracy for your application. Two or three decimal places are generally sufficient for most situations.
Q: Are there any online tools or calculators that can help with fraction-to-percentage conversions?
A: Yes, many online calculators and websites can perform fraction-to-percentage conversions. These tools can be useful for checking your work or for performing quick conversions. However, understanding the underlying mathematical principles remains crucial.
Q: Can I convert percentages back to fractions?
A: Absolutely! To convert a percentage back to a fraction, divide the percentage by 100 and simplify the resulting fraction. For example, 6.67% is approximately equivalent to 6.67/100 = 667/10000, which simplifies to approximately 1/15.
Q: What are some common mistakes to avoid when converting fractions to percentages?
A: Common mistakes include incorrectly dividing the numerator by the denominator, forgetting to multiply the decimal by 100, and rounding incorrectly. Always double-check your work and use appropriate rounding techniques.
Conclusion
Converting fractions to percentages is a vital skill with far-reaching applications. We've explored three methods for converting 5/75 to a percentage, all yielding the approximate result of 6.67%. Understanding the underlying concepts of fractions, decimals, and percentages, and practicing different conversion methods, will enhance your mathematical proficiency and problem-solving skills in various contexts. Remember to always check your work and round to an appropriate number of decimal places depending on the level of accuracy needed. Mastering this skill empowers you to confidently navigate various numerical challenges in your academic, professional, and personal life.
Latest Posts
Latest Posts
-
Examples Of Non Contact Forces
Sep 19, 2025
-
Cross Section Of Animal Cell
Sep 19, 2025
-
Number Line For Negative Numbers
Sep 19, 2025
-
Made Of Clay Crossword Clue
Sep 19, 2025
-
What Is A Principal Clause
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 5 75 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.