4 X 8 X 3
candidatos
Sep 24, 2025 · 6 min read
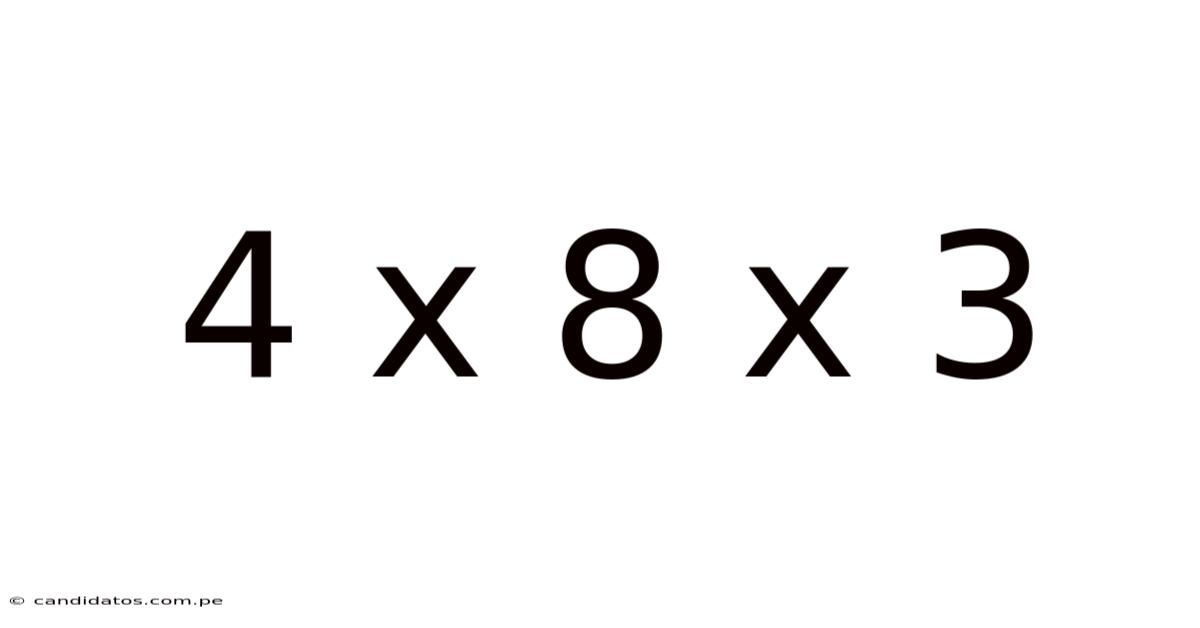
Table of Contents
Decoding 4 x 8 x 3: Exploring Dimensions, Volume, and Applications
Understanding the dimensions "4 x 8 x 3" is far more than simply recognizing three numbers; it unlocks a world of practical applications and mathematical concepts. This seemingly simple expression represents a set of dimensions, most commonly applied to describe the size of a rectangular object like a sheet of plywood, a concrete slab, or even a shipping container. This article will delve into the implications of these dimensions, exploring their volume calculation, potential applications across various industries, and the mathematical principles underlying their representation.
Understanding the Dimensions
The notation "4 x 8 x 3" represents the length, width, and height of a rectangular prism (or cuboid). In this case:
- 4 represents one dimension (e.g., length in feet, meters, or inches).
- 8 represents a second dimension (e.g., width in the same units as the length).
- 3 represents the third dimension (e.g., height in the same units as the length and width).
It's crucial to understand that the order of these numbers matters in some contexts, although for volume calculation, it doesn't affect the final result. However, if you're dealing with spatial orientation, specifying which number represents length, width, and height becomes important. For instance, in construction, understanding the orientation of a 4x8 sheet of plywood is vital for efficient cutting and material usage.
Calculating the Volume
One of the most immediate applications of these dimensions is calculating the volume of the rectangular prism. The formula for the volume (V) of a rectangular prism is:
V = Length x Width x Height
In our case:
V = 4 x 8 x 3 = 96 cubic units
The "cubic units" part is essential. It signifies that the volume is a three-dimensional measurement; the units will depend on the units used for length, width, and height. If the dimensions were in feet, the volume would be 96 cubic feet (ft³). If they were in meters, the volume would be 96 cubic meters (m³). Understanding the units is paramount for accurate calculations and practical applications.
Applications Across Industries
The dimensions 4 x 8 x 3, or variations thereof, appear in numerous industries and applications. Let's explore some key examples:
Construction and Building Materials:
- Plywood Sheets: Standard plywood sheets often come in dimensions close to 4 x 8 feet. Knowing these dimensions is fundamental for calculating the quantity needed for a project, determining cutting patterns, and optimizing material usage. The "3" in this case might represent the thickness of the plywood sheet in inches or centimeters.
- Concrete Slabs: Concrete slabs for foundations, patios, or driveways are often poured in sizes that are multiples of 4 x 8 feet. The "3" might represent the thickness of the slab in inches.
- Framing Lumber: While not perfectly matching the 4 x 8 x 3 dimensions, framing lumber sizes are often multiples or fractions of these dimensions, impacting the structural design and material calculations in building construction.
- Shipping and Packaging: Shipping containers and pallets often utilize dimensions that are multiples or fractions of these base dimensions to maximize efficiency in loading and transportation.
Manufacturing and Production:
- Machining and Fabrication: Parts in various manufacturing processes might be created with dimensions based on these numbers, dictating the size of tools, workspaces, and production processes.
- Packaging Design: Products might be packaged in boxes with dimensions related to 4 x 8 x 3, impacting storage space and shipping costs.
- Inventory Management: Warehouses and storage facilities often utilize spatial arrangements based on these dimensions for efficient storage and retrieval of goods.
Agriculture and Horticulture:
- Greenhouse Structures: The framework and internal layout of greenhouses could be designed using multiples of these basic dimensions.
- Gardening Beds: Raised garden beds or planting areas might be constructed with dimensions related to 4 x 8 x 3, influencing planting strategies and yield optimization.
Other Applications:
- Aquariums and Fish Tanks: While not a standard size, aquariums or fish tanks might be designed with dimensions influenced by these numbers.
- Custom Furniture: Carpenters and furniture makers might use these dimensions as a starting point for designing custom pieces, particularly those involving cabinetry or storage units.
- 3D Printing: Although the dimensions might need scaling, these numbers can be utilized for designing and calculating the volume of objects to be 3D printed.
Advanced Considerations: Scale, Units, and Precision
The apparent simplicity of "4 x 8 x 3" masks the importance of context and precision:
- Scale: The units of measurement are critical. 4 x 8 x 3 inches is vastly different from 4 x 8 x 3 meters. Always clarify the units to avoid errors.
- Precision: The stated dimensions may be approximations. In construction, for example, a 4 x 8 foot sheet of plywood might have slight variations in actual size due to manufacturing tolerances.
- Dimensional Analysis: When performing calculations involving these dimensions, it’s crucial to maintain consistency in units. If you’re working with a mix of units (e.g., feet and inches), convert everything to a common unit before performing calculations.
Frequently Asked Questions (FAQ)
Q: What is the surface area of a rectangular prism with dimensions 4 x 8 x 3?
A: The surface area (SA) is calculated using the formula: SA = 2(lw + lh + wh), where l, w, and h represent length, width, and height respectively. Therefore, SA = 2(4 x 8 + 4 x 3 + 8 x 3) = 2(32 + 12 + 24) = 136 square units. Again, the units (square inches, square feet, etc.) depend on the units of the dimensions.
Q: How many 1 x 1 x 1 cubic units can fit inside a 4 x 8 x 3 rectangular prism?
A: This is simply the volume of the prism, which is 96 cubic units. Therefore, 96 units of 1 x 1 x 1 size can fit inside.
Q: Can I use these dimensions to calculate the weight of an object?
A: No, you can’t determine the weight from dimensions alone. Weight depends on the density of the material. You would need to know the material's density to calculate its weight using the formula: Weight = Volume x Density.
Q: Are 4 x 8 x 3 dimensions always standard?
A: No, these are common but not universal standards. The actual dimensions used vary widely depending on the application and the industry.
Conclusion
The simple expression "4 x 8 x 3" unveils a wealth of practical applications and mathematical concepts. Understanding these dimensions is crucial in various fields, from construction and manufacturing to packaging and agriculture. By mastering the calculation of volume and understanding the importance of units and precision, you gain a valuable tool for problem-solving and decision-making in numerous real-world scenarios. Remember, while the numbers themselves are straightforward, the context and applications are vast and extend far beyond a simple arithmetic calculation. This seemingly basic concept serves as a foundation for more complex engineering, design, and logistical problems. The ability to effectively use and interpret these dimensions forms a cornerstone of understanding spatial relationships and quantitative problem-solving.
Latest Posts
Latest Posts
-
Trial Balance Format With Example
Sep 24, 2025
-
How Long Do Chameleons Live
Sep 24, 2025
-
Make An Effort Crossword Clue
Sep 24, 2025
-
Angles In A Full Turn
Sep 24, 2025
-
1 Cm Grid Graph Paper
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 4 X 8 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.