36 50 As A Percent
candidatos
Sep 16, 2025 · 5 min read
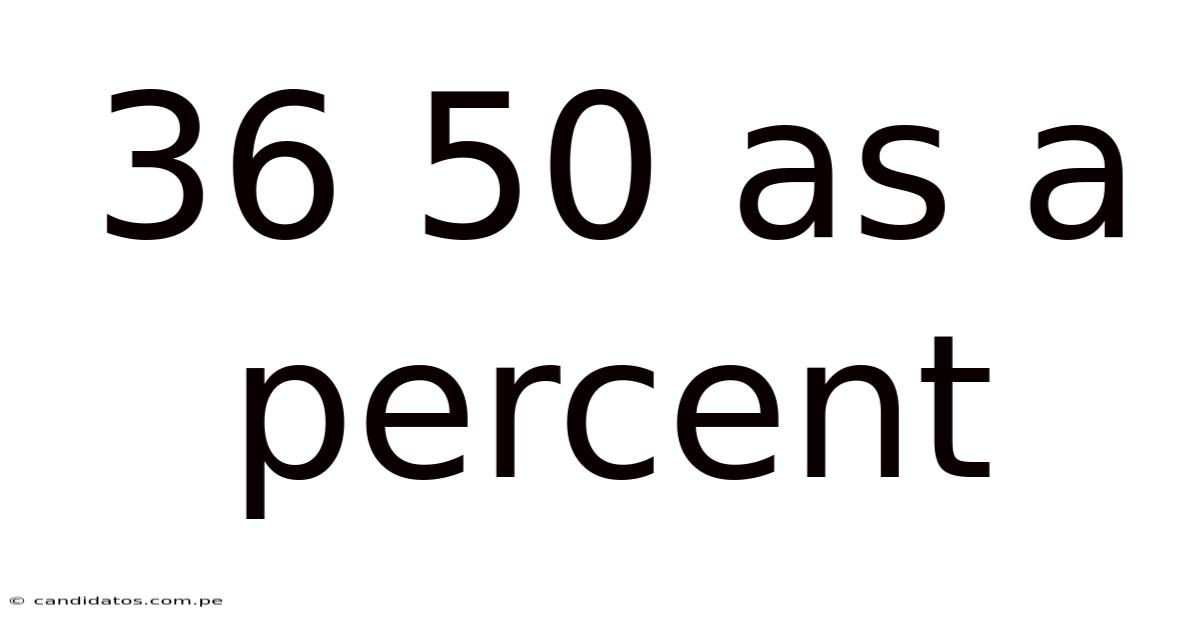
Table of Contents
36/50 as a Percent: A Comprehensive Guide to Understanding Fractions, Decimals, and Percentages
Understanding the relationship between fractions, decimals, and percentages is a fundamental skill in mathematics. This comprehensive guide will explore how to convert the fraction 36/50 into a percentage, explaining the underlying concepts and providing practical examples to solidify your understanding. We'll cover the calculation process, delve into the underlying mathematical principles, and address frequently asked questions to ensure a complete grasp of this essential concept.
Introduction: The Interplay of Fractions, Decimals, and Percentages
Fractions, decimals, and percentages are all different ways of representing parts of a whole. A fraction expresses a part of a whole as a ratio of two numbers (numerator/denominator). A decimal represents a part of a whole using a base-ten system, with a decimal point separating the whole number from the fractional part. A percentage expresses a part of a whole as a fraction of 100. Mastering the conversion between these forms is crucial for various applications, from calculating grades to understanding financial data. This guide focuses on converting the fraction 36/50 to a percentage, a common task encountered in many fields.
Method 1: Converting the Fraction to a Decimal, Then to a Percentage
This is a two-step process. First, we convert the fraction 36/50 into a decimal. Then, we convert that decimal into a percentage.
- Step 1: Converting the Fraction to a Decimal
To convert a fraction to a decimal, we divide the numerator (the top number) by the denominator (the bottom number). In this case:
36 ÷ 50 = 0.72
- Step 2: Converting the Decimal to a Percentage
To convert a decimal to a percentage, we multiply the decimal by 100 and add the percent symbol (%).
0.72 x 100 = 72%
Therefore, 36/50 is equal to 72%.
Method 2: Simplifying the Fraction First
Before converting to a decimal, simplifying the fraction can often make the calculation easier. We look for a common factor between the numerator (36) and the denominator (50). Both numbers are divisible by 2:
36 ÷ 2 = 18 50 ÷ 2 = 25
This simplifies the fraction to 18/25. Now we can convert this simplified fraction to a decimal:
18 ÷ 25 = 0.72
And then convert the decimal to a percentage:
0.72 x 100 = 72%
This method demonstrates that simplifying the fraction beforehand doesn't change the final percentage; it simply makes the calculation more straightforward.
Method 3: Direct Percentage Conversion using Proportion
This method involves setting up a proportion. We know that a percentage is a fraction out of 100. We can set up a proportion:
36/50 = x/100
To solve for 'x' (the percentage), we cross-multiply:
50x = 3600
Then, divide both sides by 50:
x = 3600 ÷ 50 = 72
Therefore, x = 72%, confirming our previous results. This method directly links the fraction to the percentage concept, highlighting the fundamental relationship between them.
Understanding the Mathematical Principles
The conversion from fractions to percentages relies on the core concept of proportionality. A percentage is simply a fraction with a denominator of 100. When we convert 36/50 to a percentage, we're essentially finding an equivalent fraction with a denominator of 100. This involves scaling the fraction up or down proportionally to maintain its value. The process of dividing the numerator by the denominator and then multiplying by 100 achieves this scaling.
Practical Applications of Percentage Calculations
Understanding how to calculate percentages like 36/50 as a percentage is essential in various real-world scenarios:
- Academic Performance: Calculating grades based on the number of correct answers out of the total questions.
- Financial Calculations: Determining interest rates, discounts, tax amounts, and profit margins.
- Statistical Analysis: Representing data proportions and distributions in charts and graphs.
- Data Interpretation: Understanding survey results, market research findings, and other data sets.
- Everyday Life: Calculating tips, sales tax, and other common financial transactions.
Further Exploration: Understanding Different Percentage Types
While we’ve focused on converting a simple fraction to a percentage, it's important to be aware of other types of percentage problems. These include:
- Calculating a percentage of a number: For instance, finding 72% of 200.
- Finding the percentage increase or decrease: Calculating the percentage change between two values.
- Calculating the original value after a percentage increase or decrease: Reversing percentage changes.
Frequently Asked Questions (FAQ)
-
Q: Can I use a calculator to convert 36/50 to a percentage?
- A: Yes, absolutely! Simply divide 36 by 50 and then multiply the result by 100. Most calculators have a percentage function that simplifies this process even further.
-
Q: Why is it important to understand how to convert fractions to percentages?
- A: This skill is essential for interpreting data, making financial calculations, and understanding various real-world scenarios involving proportions and ratios.
-
Q: What if the fraction doesn't simplify easily?
- A: Even if the fraction doesn't simplify easily, the methods outlined above (direct division and then multiplication by 100, or setting up a proportion) will still work accurately. A calculator can be particularly useful in these cases.
-
Q: Are there any other ways to convert a fraction to a percentage?
- A: Yes, you can also use the concept of proportional reasoning to set up an equation. For example, you could set up the equation: (36/50) * 100 = x, where x represents the percentage.
-
Q: What happens if the fraction is an improper fraction (numerator > denominator)?
- A: The same methods apply. The resulting percentage will be greater than 100%.
Conclusion: Mastering Percentage Conversions
Converting fractions like 36/50 into percentages is a fundamental mathematical skill with widespread applications. By understanding the different methods—converting to a decimal first, simplifying the fraction, or using direct proportion—you can confidently tackle various percentage problems. Remember, the key is understanding the underlying relationship between fractions, decimals, and percentages—they all represent parts of a whole, simply expressed in different forms. The ability to seamlessly convert between these forms empowers you to solve a vast range of problems in academic, professional, and everyday contexts. Continue practicing these methods, and you’ll quickly master the art of percentage calculations.
Latest Posts
Latest Posts
-
Words That Rhyme With Boat
Sep 16, 2025
-
Sum If Not Equal To
Sep 16, 2025
-
What Is 151cm In Feet
Sep 16, 2025
-
1000 Sq Ft To Feet
Sep 16, 2025
-
Three Digit Subtraction With Regrouping
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 36 50 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.