33 50 As A Percent
candidatos
Sep 16, 2025 · 6 min read
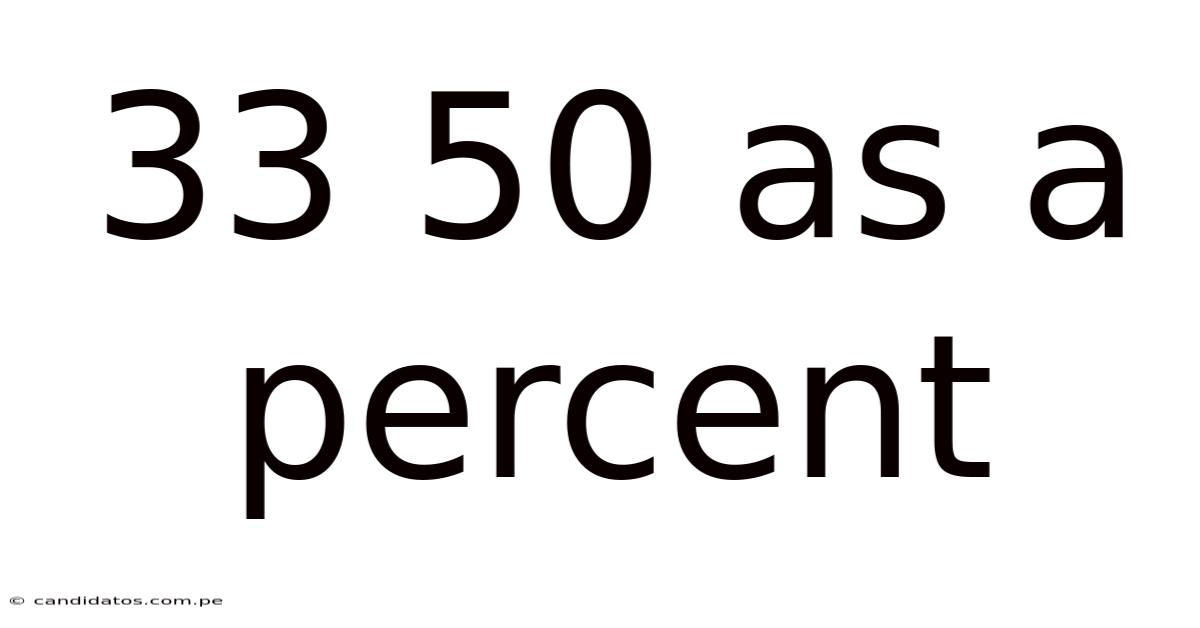
Table of Contents
33/50 as a Percent: A Comprehensive Guide to Fraction-to-Percentage Conversion
Understanding how to convert fractions to percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and tax rates to understanding statistical data and analyzing financial reports. This comprehensive guide will walk you through the process of converting the fraction 33/50 into a percentage, explaining the underlying concepts and providing practical examples. We'll delve into multiple methods, address common misconceptions, and explore the significance of percentage calculations in various contexts. By the end, you'll not only know that 33/50 is 66%, but you'll also possess a deeper understanding of percentage conversion itself.
Understanding Fractions and Percentages
Before diving into the conversion of 33/50, let's establish a clear understanding of fractions and percentages. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts you have, while the denominator indicates the total number of parts. For example, in the fraction 33/50, 33 represents the number of parts, and 50 represents the total number of equal parts.
A percentage, denoted by the symbol %, represents a fraction out of 100. It expresses a proportion as a number out of one hundred. For instance, 66% means 66 out of 100, or 66/100. Percentages are incredibly useful because they provide a standardized way to compare and understand proportions, regardless of the size of the whole.
Method 1: Converting the Fraction Directly
The most straightforward method to convert 33/50 to a percentage involves directly manipulating the fraction. The key is to transform the denominator into 100. Since percentages are expressed as parts of 100, we need to find an equivalent fraction with a denominator of 100.
To do this, we ask ourselves: "What number, when multiplied by 50, gives us 100?" The answer is 2. Therefore, we multiply both the numerator and the denominator of 33/50 by 2:
(33 x 2) / (50 x 2) = 66/100
Now that we have a fraction with a denominator of 100, we can easily express it as a percentage. The numerator, 66, directly represents the percentage. Therefore, 33/50 is equal to 66%.
Method 2: Using Decimal Conversion as an Intermediate Step
Another approach involves converting the fraction to a decimal first and then converting the decimal to a percentage. To convert 33/50 to a decimal, we simply divide the numerator (33) by the denominator (50):
33 ÷ 50 = 0.66
Now, to convert the decimal 0.66 to a percentage, we multiply it by 100:
0.66 x 100 = 66%
This method provides an alternative pathway to arrive at the same result: 33/50 is equivalent to 66%.
Method 3: Using Proportions
This method relies on setting up a proportion to solve for the unknown percentage. We can express the problem as:
33/50 = x/100
Where 'x' represents the unknown percentage. To solve for 'x', we can cross-multiply:
50x = 3300
Now, divide both sides by 50:
x = 3300 ÷ 50 = 66
Therefore, x = 66, confirming that 33/50 is 66%.
Practical Applications of Percentage Conversions
The ability to convert fractions to percentages has countless real-world applications. Here are a few examples:
- Discounts and Sales: If a store offers a 33/50 discount on an item, knowing that this equates to a 66% discount helps consumers quickly understand the savings.
- Test Scores and Grades: If a student answers 33 out of 50 questions correctly on a test, their score is 66%, providing a clear representation of their performance.
- Financial Calculations: Percentage calculations are crucial in finance, whether it's determining interest rates, calculating profit margins, or understanding investment returns. Converting fractions to percentages simplifies the interpretation of financial data.
- Statistical Analysis: In statistics, percentages are frequently used to represent proportions within a data set, facilitating comparisons and drawing meaningful conclusions.
- Everyday Life: Percentages are used to express various proportions in daily life, such as the percentage of ingredients in a recipe, the percentage of battery life remaining on a device, or the percentage of completion of a project.
Common Misconceptions and Troubleshooting
While converting fractions to percentages is relatively straightforward, some common misconceptions can lead to errors:
- Forgetting to multiply by 100: A frequent mistake is to stop after converting the fraction to a decimal. Remember that a decimal needs to be multiplied by 100 to obtain the percentage.
- Incorrectly interpreting the fraction: Ensure you understand which number represents the part and which represents the whole before attempting the conversion.
- Rounding Errors: When dealing with decimals that have many digits after the decimal point, rounding can introduce small errors. It's best practice to carry out calculations with as much precision as possible before rounding the final result.
Frequently Asked Questions (FAQ)
Q1: Can I convert any fraction to a percentage?
A1: Yes, any fraction can be converted to a percentage using the methods described above. However, some fractions may result in percentages with recurring decimals (e.g., 1/3 = 33.333...).
Q2: What if the denominator of the fraction is not easily divisible to reach 100?
A2: If the denominator doesn't easily convert to 100, you can still use the decimal conversion method. Divide the numerator by the denominator to obtain the decimal, and then multiply by 100 to find the percentage.
Q3: Are there any online tools or calculators to help with fraction-to-percentage conversions?
A3: While this article focuses on manual calculation methods, numerous online calculators are available that can quickly convert fractions to percentages. These tools can be particularly helpful for more complex fractions or for verifying your own calculations.
Q4: What's the difference between a percentage and a ratio?
A4: While both percentages and ratios express proportions, a percentage is always a fraction out of 100, whereas a ratio can compare any two quantities. A ratio can be converted into a percentage, but not all ratios are percentages.
Q5: How can I improve my understanding of percentage calculations?
A5: Practice is key! Try converting various fractions to percentages using different methods. Start with simple fractions and gradually work towards more complex ones. Utilize online resources and practice exercises to reinforce your understanding.
Conclusion
Converting fractions to percentages is a crucial skill with wide-ranging applications in various aspects of life. This guide has presented three different methods for converting 33/50 to a percentage, all leading to the same answer: 66%. Understanding the underlying concepts and practicing different methods will strengthen your mathematical abilities and equip you to confidently handle percentage calculations in any situation. Remember the importance of understanding the fundamentals of fractions and decimals, as these are the building blocks for successful percentage conversion. By mastering this skill, you'll unlock a powerful tool for understanding and interpreting data in countless contexts.
Latest Posts
Latest Posts
-
Year 12 English Standard Syllabus
Sep 16, 2025
-
Sodium Carbonate And Sulfuric Acid
Sep 16, 2025
-
Bid Price And Offer Price
Sep 16, 2025
-
Rarest Thing In The World
Sep 16, 2025
-
Number Of Protons In Potassium
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 33 50 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.