32 Out Of 45 Percent
candidatos
Sep 21, 2025 · 5 min read
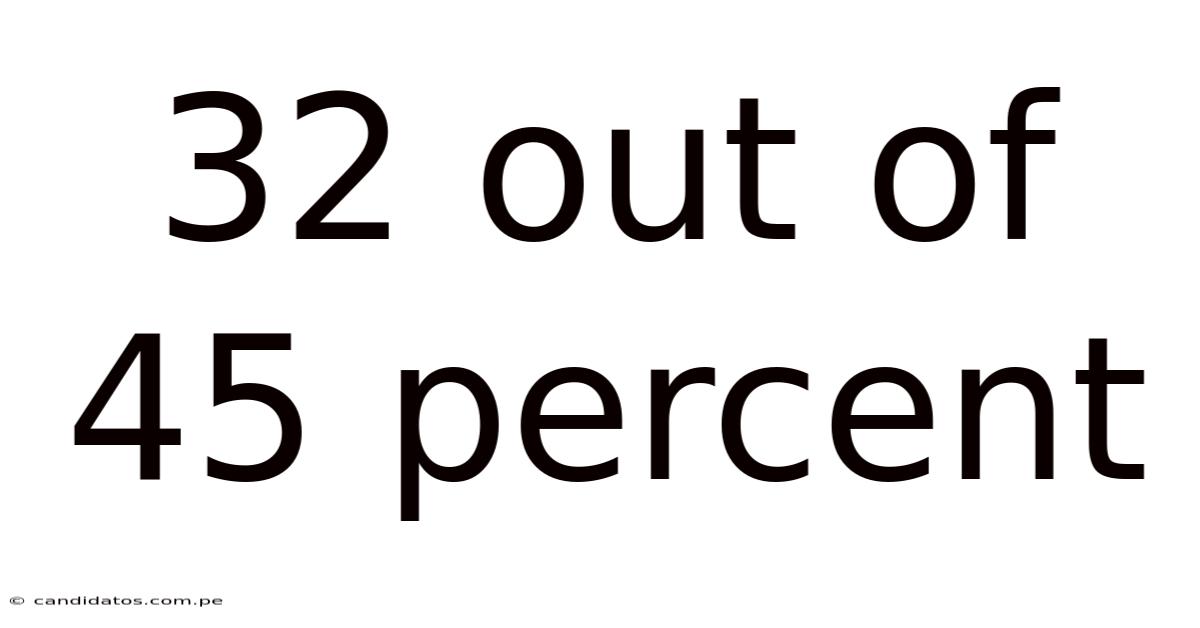
Table of Contents
Decoding 32 out of 45: Percentage, Fraction, and Real-World Applications
Understanding percentages is a fundamental skill applicable across numerous fields, from academic assessments to financial calculations and everyday decision-making. This article delves into the meaning and implications of "32 out of 45," exploring its representation as a percentage, fraction, and demonstrating its practical relevance through diverse examples. We'll also look at how to calculate this and similar scenarios, equipping you with the tools to confidently tackle percentage problems in any context.
Introduction: Understanding the Core Concept
The statement "32 out of 45" signifies a ratio: 32 represents a part of a larger whole, 45. To understand its significance, we must convert this ratio into a more easily interpretable form, primarily a percentage. Percentages express portions of a whole as a fraction of 100. This standardized format simplifies comparisons and facilitates understanding across different scales.
1. Calculating the Percentage:
The process of converting "32 out of 45" into a percentage involves two simple steps:
-
Step 1: Divide the part by the whole: Divide 32 (the part) by 45 (the whole): 32 ÷ 45 ≈ 0.711
-
Step 2: Multiply by 100: Multiply the result from Step 1 by 100 to express it as a percentage: 0.711 × 100 ≈ 71.1%
Therefore, 32 out of 45 represents approximately 71.1%. This signifies that 32 constitutes roughly 71.1% of the total 45.
2. Representing as a Fraction:
The ratio "32 out of 45" can also be represented as a fraction: 32/45. This fraction is already in its simplest form because 32 and 45 share no common factors other than 1. This fractional representation offers an alternative, yet equally valid, way of expressing the same proportion.
3. Real-World Applications: Where Percentages Matter
Understanding percentages is crucial in various real-world scenarios. Let's explore some examples illustrating the practical application of the 71.1% derived from "32 out of 45":
-
Academic Performance: Imagine a student scoring 32 out of 45 marks on a test. Their score translates to 71.1%, which provides a clear indication of their performance relative to the total possible marks. This percentage helps in grading, comparing performance across students, and identifying areas for improvement.
-
Business and Finance: In business, percentages are fundamental for analyzing sales figures, market share, profit margins, and growth rates. For example, if a company planned to sell 45 units of a product and managed to sell 32, the sales performance would be 71.1%. This data helps businesses track progress, assess the effectiveness of marketing strategies, and make informed decisions about future operations.
-
Surveys and Statistics: Percentages are crucial in interpreting survey results and statistical data. If 32 out of 45 respondents to a survey indicated a preference for a particular product, this represents a 71.1% preference rate. This data helps businesses understand consumer sentiment, tailor their products and services accordingly, and make more effective marketing decisions.
-
Everyday Calculations: Percentages are frequently encountered in everyday situations, such as calculating discounts, tips, tax rates, or interest on loans. For instance, a 71.1% discount on an item would significantly reduce its price. Understanding these percentages helps consumers make informed decisions about purchases and manage their finances.
4. Beyond 32 out of 45: Mastering Percentage Calculations
The principles applied to calculating "32 out of 45" are universally applicable to any ratio. Let's explore a more general approach:
To calculate the percentage for any "X out of Y" scenario:
- Divide X by Y: X ÷ Y = Z
- Multiply Z by 100: Z × 100 = Percentage (%)
This formula provides a flexible tool for calculating percentages in diverse contexts.
5. Understanding Different Percentage Scenarios
While calculating the percentage for "32 out of 45" is straightforward, consider these variations to solidify your understanding:
-
Finding the part: If you know the percentage and the whole, you can find the part. For example, what is 71.1% of 45? (45 x 0.711 ≈ 32)
-
Finding the whole: If you know the part and the percentage, you can find the whole. For example, if 32 represents 71.1%, what is the total? (32 ÷ 0.711 ≈ 45)
6. Advanced Applications and Interpretations
Beyond basic calculations, understanding percentages involves appreciating the nuances and potential misinterpretations.
-
Context Matters: A 71.1% score on a difficult exam might be considered excellent, whereas a 71.1% success rate in a simple task might be disappointing. The context significantly influences the interpretation of the percentage.
-
Comparing Percentages: When comparing percentages, ensure they refer to the same base. Comparing percentages from different sample sizes or contexts can be misleading.
-
Margin of Error: In statistical analyses, the margin of error must be considered. A 71.1% approval rating with a large margin of error offers less certainty than a similar rating with a small margin of error.
7. Frequently Asked Questions (FAQ)
-
Q: What is the simplest way to calculate a percentage?
- A: Divide the part by the whole and multiply by 100.
-
Q: Can I use a calculator for percentage calculations?
- A: Absolutely! Calculators are efficient tools for percentage calculations, especially for complex scenarios.
-
Q: What if I get a decimal in my percentage?
- A: Decimals in percentages are common and perfectly acceptable. You can round to a reasonable number of decimal places depending on the context (e.g., 71.1% instead of 71.111%).
-
Q: How do I convert a fraction to a percentage?
- A: Divide the numerator by the denominator and multiply by 100.
-
Q: Are there online tools to help with percentage calculations?
- A: Yes, many websites and apps provide percentage calculators.
8. Conclusion: Mastering Percentages for Life's Challenges
Understanding percentages is a versatile skill with far-reaching applications. From academic assessments to financial decision-making, the ability to calculate and interpret percentages empowers you to make informed choices, analyze data effectively, and navigate various aspects of life with greater confidence. By grasping the fundamental principles and practicing different scenarios, you can build a strong foundation in this essential mathematical skill, enabling you to tackle percentage problems with ease and accuracy. Remember the core principles – divide the part by the whole and multiply by 100 – and you'll be well-equipped to handle any percentage calculation you encounter. Practice regularly, explore different applications, and you'll soon find that percentages become an intuitive and valuable tool in your arsenal.
Latest Posts
Latest Posts
-
Left Handed Bow And Arrow
Sep 21, 2025
-
Iron Iii Nitrate Potassium Thiocyanate
Sep 21, 2025
-
Words That Rhyme With 5
Sep 21, 2025
-
Chemical Formula For Sodium Sulfate
Sep 21, 2025
-
Venn Diagram Eukaryotes And Prokaryotes
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 32 Out Of 45 Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.