32 100 As A Percentage
candidatos
Sep 18, 2025 · 6 min read
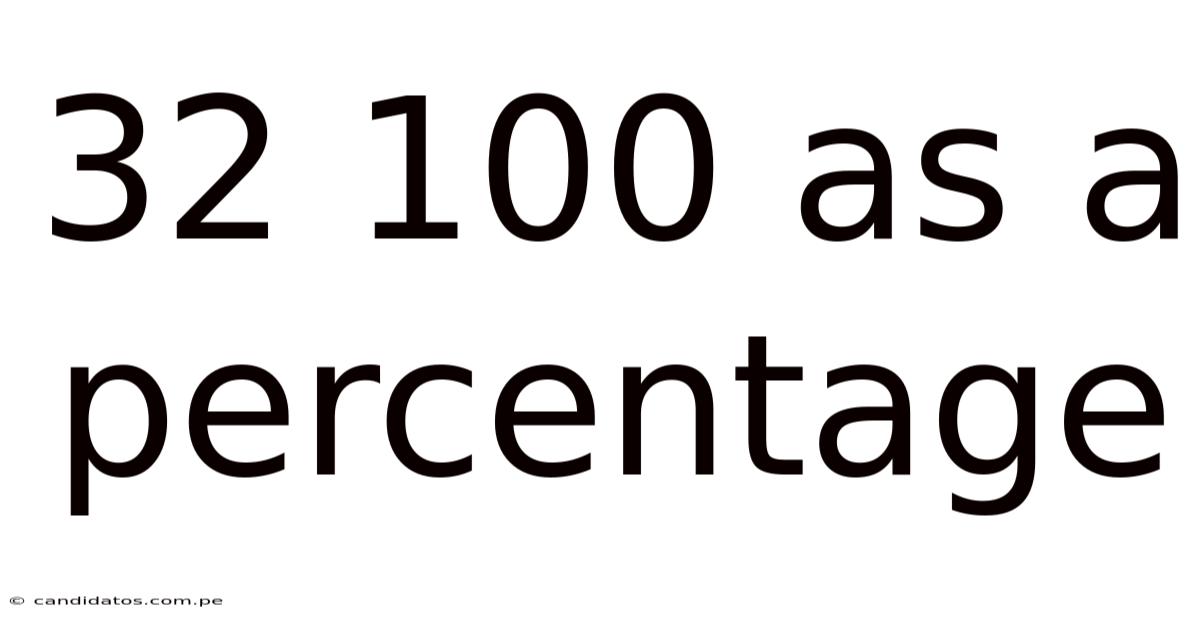
Table of Contents
Understanding 32 out of 100 as a Percentage: A Comprehensive Guide
Understanding percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and taxes to analyzing data and interpreting statistics. This article will comprehensively explore how to express 32 out of 100 as a percentage, delve into the underlying mathematical concepts, and provide practical examples to solidify your understanding. We'll also address common misconceptions and answer frequently asked questions. This guide is designed to be accessible to everyone, from students learning about percentages for the first time to those seeking a refresher on the topic.
What is a Percentage?
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of 100" (from the Latin "per centum"). Percentages are denoted by the symbol "%". They are used to represent proportions or ratios, making comparisons and calculations easier to understand. For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Calculating 32 out of 100 as a Percentage
Converting a fraction to a percentage is a straightforward process. In this case, we have the fraction 32/100. Since a percentage is a fraction out of 100, this conversion is particularly simple:
-
Step 1: Identify the fraction: We are given the fraction 32/100. This represents 32 parts out of a total of 100 parts.
-
Step 2: Convert the fraction to a decimal: To convert a fraction to a decimal, divide the numerator (the top number) by the denominator (the bottom number). In this case, 32 ÷ 100 = 0.32.
-
Step 3: Convert the decimal to a percentage: To convert a decimal to a percentage, multiply the decimal by 100 and add the "%" symbol. So, 0.32 × 100 = 32%.
Therefore, 32 out of 100 is equal to 32%.
Practical Applications of Percentages: Real-world Examples
Understanding percentages is crucial for navigating numerous real-world situations. Here are a few examples:
-
Discounts: A store offers a 32% discount on an item. This means you save 32 cents for every dollar the item originally cost.
-
Taxes: Sales tax is often expressed as a percentage. A 6% sales tax on a $100 item would be $6 (6% of $100).
-
Grades: In many educational systems, grades are expressed as percentages, representing the proportion of correct answers on a test or the overall performance in a course. A score of 32 out of 100 would be a 32% grade.
-
Statistics: Percentages are frequently used to represent data in surveys, polls, and other statistical analyses. For instance, a survey might show that 32% of respondents prefer a particular brand.
-
Financial calculations: Interest rates on loans and savings accounts are usually expressed as percentages. Understanding these percentages is vital for making informed financial decisions.
-
Data representation: Charts and graphs often use percentages to visually represent proportions of data. A pie chart, for example, might divide a whole into segments representing percentages of different categories.
Beyond 32/100: Calculating Other Percentages
The method used to calculate 32/100 as a percentage can be applied to any fraction. Let's look at some examples:
-
To calculate the percentage for 15 out of 25:
- Express the fraction: 15/25
- Convert to a decimal: 15 ÷ 25 = 0.6
- Convert to a percentage: 0.6 × 100 = 60%
-
To calculate the percentage for 7 out of 50:
- Express the fraction: 7/50
- Convert to a decimal: 7 ÷ 50 = 0.14
- Convert to a percentage: 0.14 × 100 = 14%
-
To calculate the percentage for 12 out of 30:
- Express the fraction: 12/30
- Simplify the fraction (optional but helpful): 12/30 = 2/5
- Convert to a decimal: 2 ÷ 5 = 0.4
- Convert to a percentage: 0.4 × 100 = 40%
Understanding Percentage Change
Another crucial aspect of percentages is understanding percentage change. This calculates the relative change between two values. The formula for percentage change is:
[(New Value - Old Value) / Old Value] × 100
For example, if a price increases from $50 to $65, the percentage change is:
[(65 - 50) / 50] × 100 = 30%
This represents a 30% increase. A decrease would result in a negative percentage change.
Advanced Percentage Calculations
While calculating percentages from fractions out of 100 is relatively simple, more complex calculations might involve finding a percentage of a number, or working backward from a percentage to find an original value.
-
Finding a percentage of a number: To find, say, 32% of 200, multiply 200 by 0.32 (the decimal equivalent of 32%). 200 × 0.32 = 64.
-
Finding the original value from a percentage: If 32% of a number is 64, divide 64 by 0.32 to find the original number. 64 ÷ 0.32 = 200.
Frequently Asked Questions (FAQ)
Q1: What if the fraction isn't out of 100?
A: If the denominator is not 100, you still follow the same steps. Divide the numerator by the denominator to get a decimal, then multiply by 100 to convert to a percentage.
Q2: How do I calculate percentages in my head quickly?
A: Practice is key! Familiarize yourself with common percentage equivalents (e.g., 50% = 1/2, 25% = 1/4, 10% = 1/10). You can also use estimation techniques to quickly approximate percentages.
Q3: Are there any online calculators for percentages?
A: Yes, many online calculators are available to assist with percentage calculations. These tools can be helpful for double-checking your work or for more complex calculations.
Q4: What are some common mistakes to avoid when working with percentages?
A: A common mistake is confusing percentage change with absolute change. Another is incorrectly applying percentage calculations, particularly when dealing with compound percentages or percentage increases/decreases over multiple periods.
Q5: How can I improve my understanding of percentages?
A: Practice regularly with various problems, focusing on understanding the underlying concepts. Use real-world examples to relate the concepts to practical applications. Seek help from teachers, tutors, or online resources when needed.
Conclusion
Understanding 32 out of 100 as a percentage—which is 32%—is a stepping stone to mastering a fundamental mathematical concept. This article has provided a detailed explanation of how to calculate percentages, highlighted practical applications, and addressed common questions. Remember that consistent practice and understanding the underlying principles are vital for mastering this skill. By applying the methods and strategies discussed here, you can confidently tackle various percentage-related problems in your daily life and academic pursuits. The ability to work with percentages is a valuable skill that will serve you well across many different fields and situations.
Latest Posts
Latest Posts
-
3 4 Of 1 Meter
Sep 18, 2025
-
How Do You Grow Sprouts
Sep 18, 2025
-
How To Plant Potatoes Sprouted
Sep 18, 2025
-
700 Sq Ft In Meters
Sep 18, 2025
-
Area Of Non Right Triangle
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 32 100 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.