3 1 4 X 4
candidatos
Sep 23, 2025 · 6 min read
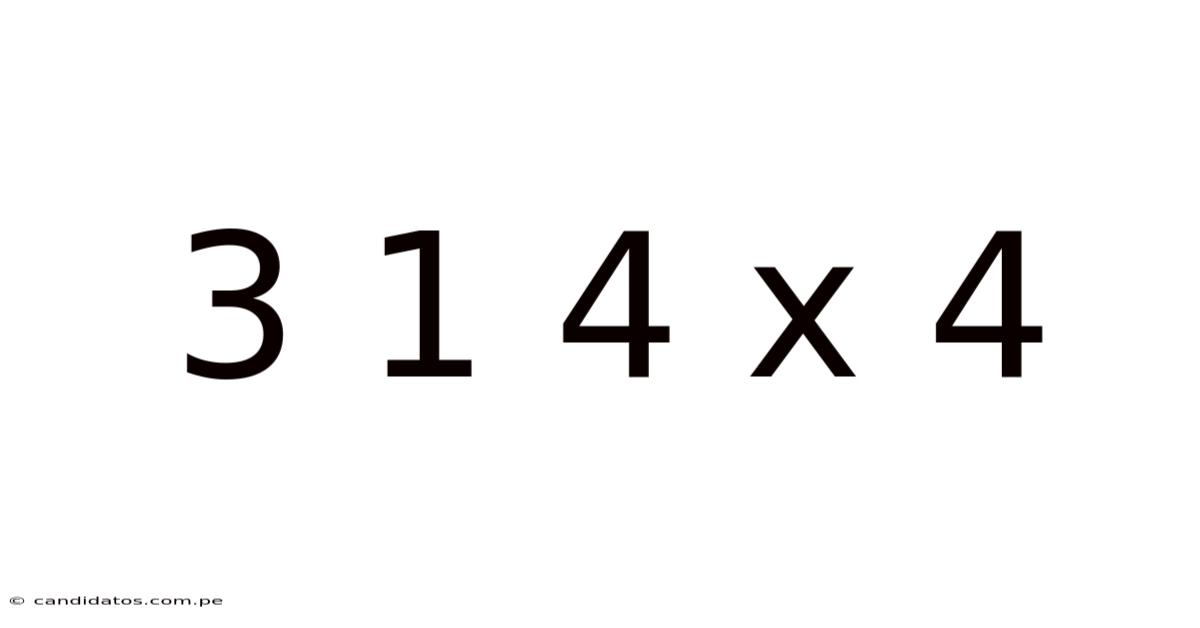
Table of Contents
Decoding the Mystery: A Deep Dive into 3x1x4 and its Applications
The seemingly simple expression "3x1x4" might initially seem unremarkable. However, depending on the context, this sequence of numbers can represent a wide array of concepts, from simple dimensions to complex mathematical problems or even representational models in various fields. This article will explore the diverse interpretations and applications of "3x1x4," delving into its mathematical implications, potential uses in design and engineering, and even its relevance in other fields like data representation and puzzle-solving. We'll unravel its mysteries and uncover its hidden potential, offering a comprehensive understanding for readers of various backgrounds.
Understanding the Basics: Dimensions and Spatial Representation
At its most fundamental level, "3x1x4" can be interpreted as a set of dimensions. This interpretation suggests a three-dimensional object with length 3 units, width 1 unit, and height 4 units. This could represent anything from a simple rectangular prism (or cuboid) to a more complex structure depending on the unit of measurement (e.g., centimeters, meters, inches). Visualizing this helps establish a basic understanding which we can build upon. Imagine a rectangular box; this notation gives us its exact measurements. This basic interpretation is crucial for understanding further applications.
Mathematical Interpretations and Calculations
Beyond simple dimensional representation, "3x1x4" can be subjected to various mathematical operations.
-
Volume Calculation: In the context of the rectangular prism described above, "3x1x4" immediately allows us to calculate the volume. The volume is simply the product of the three dimensions: 3 x 1 x 4 = 12 cubic units. This is a fundamental calculation in geometry and has wide-ranging applications in areas such as packaging design, construction, and even fluid dynamics.
-
Surface Area Calculation: Calculating the surface area requires a more detailed approach. We need to find the area of each face of the rectangular prism and then sum them. The surface area will be: 2(3x1) + 2(3x4) + 2(1x4) = 6 + 24 + 8 = 38 square units. This calculation is essential for determining the amount of material needed to construct a container or cover a surface.
-
Ratio and Proportion: The numbers 3, 1, and 4 can also be viewed as a ratio, representing proportions. This could be useful in various contexts, such as mixing ingredients in a recipe (3 parts of one ingredient, 1 part of another, and 4 parts of a third). This ratio can be scaled up or down while maintaining the same proportions. Understanding ratios is fundamental to many areas, including chemistry, cooking, and even finance.
-
Factorization and Prime Numbers: While not directly related to the spatial representation, analyzing the prime factorization of these numbers can be insightful. 3 is a prime number; 1 is neither prime nor composite; and 4 is 2². This can be important in number theory and related mathematical fields.
Applications in Design and Engineering
The interpretation of "3x1x4" as dimensions has profound implications in design and engineering.
-
Structural Design: In architectural and structural engineering, these dimensions could represent the size of a beam, column, or other structural element. Understanding the dimensions is critical for calculating load-bearing capacity, stress distribution, and overall structural integrity. The choice of these specific dimensions might be dictated by specific engineering requirements and material properties.
-
Mechanical Design: In mechanical engineering, "3x1x4" could denote the size of a component, such as a part in a machine or a piece of equipment. Precision in dimensions is paramount to ensure proper functionality and compatibility with other parts. Tolerance levels, which represent acceptable deviations from the stated dimensions, are also crucial aspects of mechanical design.
-
Packaging and Logistics: In the packaging and logistics industry, these dimensions are vital for determining the size of containers, optimizing space utilization in shipping, and calculating freight costs. Efficient packaging minimizes wasted space and reduces transportation expenses. Understanding cubic measurements and surface area calculations is essential for efficient operations.
-
Industrial Design: "3x1x4" might represent the dimensions of a product or part of a product in industrial design. Considerations beyond functionality also come into play; aesthetics and user experience play a crucial role in designing products which are both effective and appealing.
Beyond the Physical: Data Representation and Other Applications
The sequence "3x1x4" can also transcend physical dimensions and find relevance in less tangible domains.
-
Data Representation: In computer science and data analysis, this sequence could represent an array, a vector, or a specific data structure. Each number could correspond to a specific attribute or data point. Understanding how data is structured is fundamental to processing and interpreting it efficiently.
-
Game Development and Simulation: In game development and simulations, "3x1x4" could represent the size of a game object, a map section, or a specific parameter within the game environment. The precision and accuracy of these numbers are key to creating a realistic and immersive game experience.
-
Project Management: In project management, this sequence could represent a simplified breakdown of project tasks, resources, or deadlines. Each number could represent a different aspect of the project, allowing for a streamlined overview and efficient management.
-
Puzzle Solving: Consider the sequence as part of a larger puzzle or code. Analyzing the numerical relationships within this sequence could be a crucial step towards solving a more complex problem.
Frequently Asked Questions (FAQ)
-
What are the units of measurement for 3x1x4? The units are not specified; they could be centimeters, meters, inches, feet, or any other relevant unit. The context of the problem defines the units.
-
Can the order of numbers (3x1x4) be changed? Changing the order will result in a different shape with a different volume and surface area. For example, 4x1x3 would still have the same volume (12 cubic units) but different surface area and dimensions.
-
What if one of the numbers is zero? If any of the numbers is zero, it implies that the object has no extension in that dimension, resulting in a two-dimensional or one-dimensional object. For example, 3x0x4 would represent a rectangle.
-
How does this relate to other mathematical concepts? This relates to concepts like volume, surface area, ratios, proportions, and even more advanced geometrical concepts when applied to more complex shapes.
Conclusion: The Versatility of a Simple Sequence
The seemingly simple sequence "3x1x4" reveals itself as a surprisingly versatile concept. Its applications span across numerous fields, from straightforward geometric calculations to more complex scenarios in engineering, design, data representation, and even problem-solving. Understanding its diverse interpretations empowers us to approach problems from different perspectives and utilize its potential in various contexts. The key takeaway is the flexibility and adaptability of this simple numerical sequence, proving that even the most basic elements can hold significant meaning and application when viewed through the right lens. Its simplicity belies its inherent power and potential for problem-solving. The ability to interpret and apply this sequence effectively highlights the importance of fundamental mathematical concepts and their profound impact on a wide range of disciplines. This exploration underscores the value of critical thinking and analytical skills in extracting meaning and utility from even the most seemingly basic pieces of information.
Latest Posts
Latest Posts
-
Define Equality Before The Law
Sep 23, 2025
-
Calculating Mechanical Advantage Of Pulleys
Sep 23, 2025
-
Sample Of Letter Of Authority
Sep 23, 2025
-
1 12 Into A Decimal
Sep 23, 2025
-
How To Integrate A Fraction
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 3 1 4 X 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.