27 20 As A Percentage
candidatos
Sep 21, 2025 · 6 min read
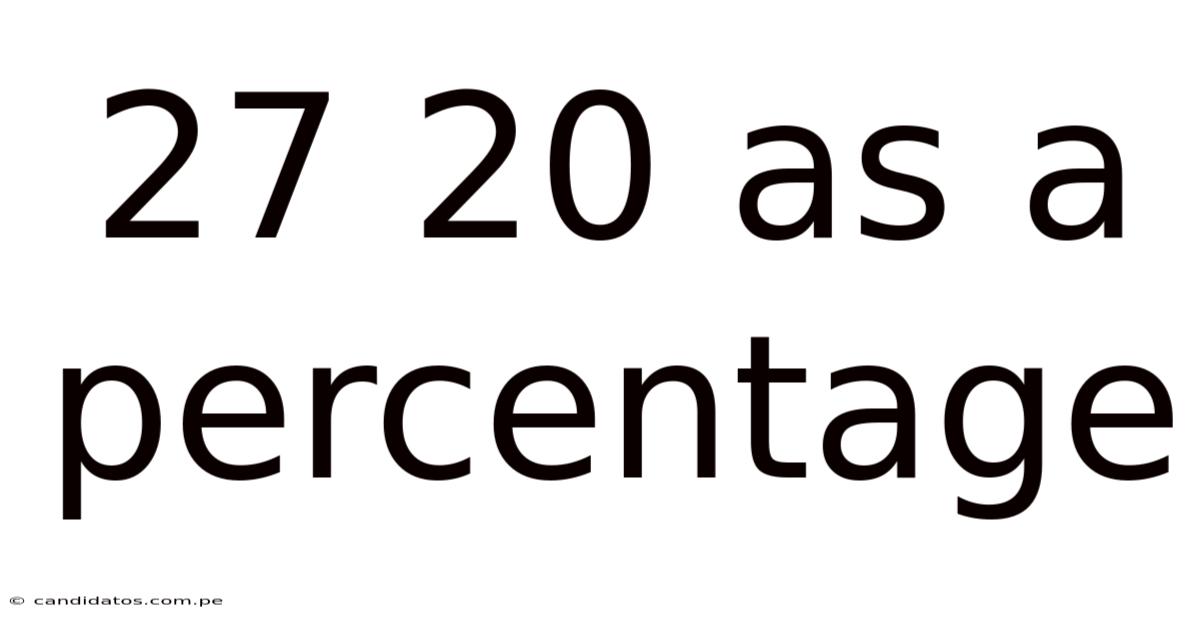
Table of Contents
Decoding 27/20 as a Percentage: A Deep Dive into Fractions, Percentages, and Their Applications
Understanding percentages is a fundamental skill in various aspects of life, from calculating discounts and taxes to interpreting statistics and analyzing data. This article delves deep into converting fractions to percentages, using the example of 27/20, and explores the broader applications of this mathematical concept. We'll cover the process step-by-step, explain the underlying principles, and address common questions and misconceptions. By the end, you'll not only know how to calculate 27/20 as a percentage but also possess a solid understanding of the relationship between fractions and percentages.
Understanding Fractions and Percentages
Before we tackle 27/20, let's briefly review the concepts of fractions and percentages. A fraction represents a part of a whole. It's expressed as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). For example, in the fraction 27/20, 27 is the numerator and 20 is the denominator. This fraction signifies that we have 27 parts out of a total of 20 parts. Notice that this is an improper fraction – the numerator is larger than the denominator, indicating a value greater than one.
A percentage, denoted by the symbol %, represents a fraction of 100. It expresses a proportion out of a hundred. For instance, 50% means 50 out of 100, or 50/100, which simplifies to 1/2. Percentages are widely used because they provide a standardized way to compare and understand proportions.
Converting 27/20 to a Percentage: A Step-by-Step Guide
Converting a fraction to a percentage involves two key steps:
-
Convert the fraction to a decimal: To do this, divide the numerator by the denominator. In our case, we divide 27 by 20:
27 ÷ 20 = 1.35
-
Convert the decimal to a percentage: Multiply the decimal by 100 and add the percentage symbol (%).
1.35 × 100 = 135%
Therefore, 27/20 as a percentage is 135%.
Why is the Percentage Greater than 100%?
The result, 135%, might seem unusual at first glance. Percentages are often perceived as being between 0% and 100%. However, percentages can exceed 100% when the fraction is an improper fraction (numerator > denominator), as in this case. This simply means that the value represented by the fraction is greater than the whole. Imagine having 27 slices of pizza when you only expected 20. You have more than the initial expectation (100%). The extra 35% represents the excess.
Real-world Applications of Percentages Greater Than 100%
Percentages exceeding 100% are common in various real-world scenarios:
- Growth and Increase: If a company's revenue increases from $20 million to $27 million, the percentage increase is 135% [(27-20)/20 * 100%].
- Overachievement: If a sales target was $20,000 and the actual sales reached $27,000, the sales team exceeded the target by 135%.
- Inflation: If the price of an item increased by more than its original value, the price inflation would be represented by a percentage greater than 100%.
- Financial Returns: Investment returns often exceed 100% in periods of rapid growth.
Different Methods for Converting Fractions to Percentages
While the division-then-multiplication method is straightforward, there's an alternative approach:
-
Find an equivalent fraction with a denominator of 100: To do this, you find a number that, when multiplied by the denominator (20), gives you 100. In this case, that number is 5 (20 x 5 = 100).
-
Multiply both the numerator and denominator by that number:
(27 x 5) / (20 x 5) = 135/100
-
The numerator of the equivalent fraction is the percentage: Since 135/100 represents 135 out of 100, the percentage is 135%.
This method is particularly helpful when the denominator is a factor of 100 (e.g., 10, 20, 25, 50).
Understanding the Concept of Ratio and Proportion
The conversion of fractions to percentages is fundamentally about understanding ratios and proportions. A ratio compares two quantities, while a proportion states that two ratios are equal. In our example, 27/20 is a ratio, and the equation 27/20 = 135/100 is a proportion. The proportion highlights that 27 parts out of 20 is equivalent to 135 parts out of 100.
Percentage Increase and Decrease Calculations
Related to percentage calculations are the concepts of percentage increase and percentage decrease. These calculations are frequently used to quantify changes in values over time. The formula for percentage increase is:
[(New Value - Old Value) / Old Value] x 100%
For percentage decrease, the formula is:
[(Old Value - New Value) / Old Value] x 100%
For example, if the old value is 20 and the new value is 27, the percentage increase is:
[(27 - 20) / 20] x 100% = 35%
This highlights that while 27/20 represents a 135% value relative to 20, the increase from 20 to 27 is 35%. It's crucial to understand the context and the appropriate calculation to use.
Frequently Asked Questions (FAQ)
-
Can percentages be negative? Yes, percentages can be negative, indicating a decrease or loss. For example, a -10% change implies a decrease of 10%.
-
What if the denominator of the fraction is zero? Division by zero is undefined in mathematics. A fraction with a zero denominator is meaningless.
-
Are there any online calculators for converting fractions to percentages? Yes, many online calculators are available that can quickly convert fractions to percentages. However, understanding the underlying principles is crucial for applying the concept effectively in various situations.
-
How are percentages used in finance? Percentages are fundamental in finance for calculating interest rates, returns on investment, profit margins, and various financial ratios.
-
How are percentages used in statistics? Percentages are used extensively in statistics to represent proportions of data, such as calculating percentages of respondents in a survey who answered a particular question in a specific way, or to express the likelihood of an event (probability).
Conclusion
Converting 27/20 to a percentage results in 135%. This article provides a detailed walkthrough of the conversion process, explains the rationale behind percentages greater than 100%, and illustrates the concept's broad application in various fields. Mastering percentage calculations is essential for anyone who needs to interpret data, analyze trends, or make informed decisions in various contexts. Understanding the relationship between fractions, decimals, and percentages empowers you to tackle a wide range of mathematical problems and real-world challenges with confidence. Remember that while calculators can simplify the process, a solid grasp of the underlying principles enhances your problem-solving abilities and fosters a deeper understanding of mathematical concepts.
Latest Posts
Latest Posts
-
Pictures Of Fruit And Vegetables
Sep 21, 2025
-
Difference Between Nucleus And Nucleolus
Sep 21, 2025
-
6 7 In A Decimal
Sep 21, 2025
-
The Oxford Dictionary Of Proverbs
Sep 21, 2025
-
Decreasing At A Decreasing Rate
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 27 20 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.