26 Out Of 45 Percentage
candidatos
Sep 16, 2025 · 5 min read
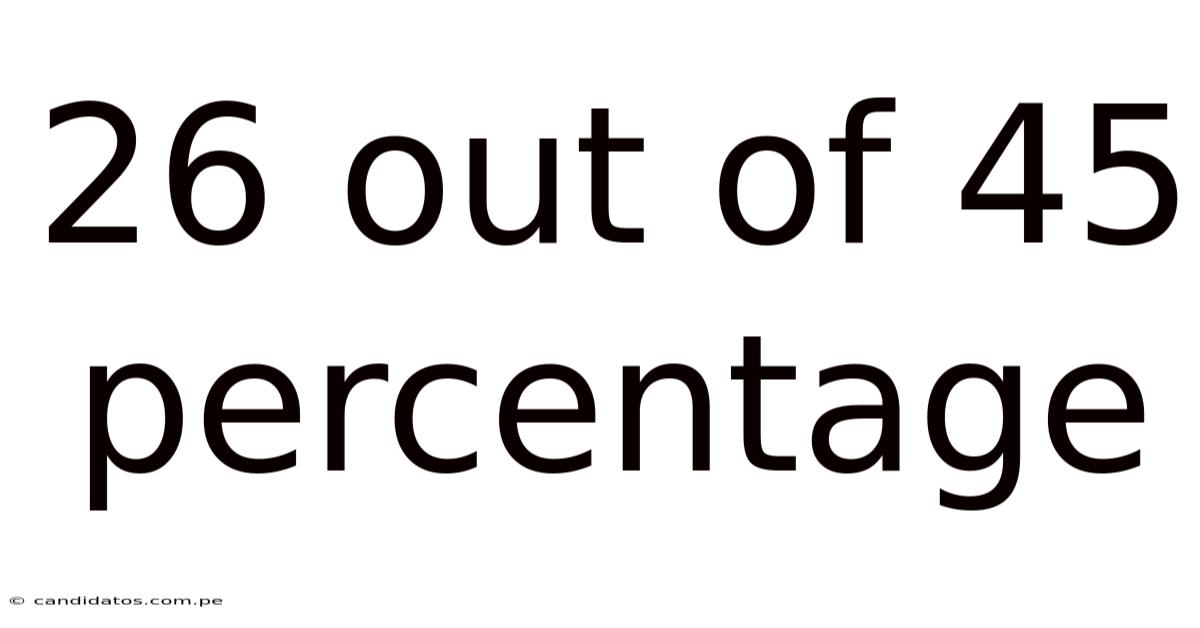
Table of Contents
Decoding 26 out of 45: Understanding Percentages and Their Context
Understanding percentages is a fundamental skill applicable across numerous fields, from academic assessments to financial calculations and everyday decision-making. This article delves into the meaning of 26 out of 45 as a percentage, exploring its calculation, interpretation, and practical applications. We'll also address common misconceptions and provide examples to solidify your understanding. By the end, you'll not only know how to calculate this specific percentage but also possess a stronger grasp of percentage calculations in general.
What Does 26 out of 45 Represent?
The phrase "26 out of 45" represents a part-to-whole relationship. It indicates that 26 items represent a portion of a larger group containing 45 items. To understand its significance, we need to express this ratio as a percentage. Percentages are essentially fractions expressed as parts of 100. This conversion allows for easier comparison and interpretation across different datasets.
Calculating the Percentage: A Step-by-Step Guide
Calculating the percentage equivalent of 26 out of 45 involves a straightforward process:
-
Form a Fraction: Express the part (26) as the numerator and the whole (45) as the denominator of a fraction: 26/45.
-
Convert to Decimal: Divide the numerator (26) by the denominator (45). This gives us the decimal equivalent of the fraction: 26 ÷ 45 ≈ 0.5778
-
Convert to Percentage: Multiply the decimal value by 100 to express it as a percentage: 0.5778 x 100 ≈ 57.78%
Therefore, 26 out of 45 is approximately 57.78%.
Understanding the Result: Context is Key
The numerical value of 57.78% on its own is relatively meaningless. Its interpretation depends entirely on the context in which it appears. For instance:
-
Academic Performance: If 26 represents the number of correct answers out of 45 questions on a test, a score of 57.78% might be considered a passing grade in some systems, but failing in others. The context of the grading system is crucial.
-
Sales Figures: If 26 represents the number of units sold out of a total of 45 units produced, a 57.78% sales rate might indicate strong demand or potential inventory issues, depending on the industry and business goals. Analyzing sales trends over time provides additional insight.
-
Survey Results: If 26 out of 45 respondents answered "yes" to a survey question, the 57.78% positive response could point to a significant trend or public opinion. However, the size of the sample group (45) should be considered to evaluate the statistical significance of the results.
-
Project Completion: If 26 tasks are completed out of a total of 45 tasks in a project, the 57.78% completion rate suggests the project is more than halfway done, but further analysis is needed to assess whether it's on schedule and within budget.
Beyond the Calculation: Exploring Related Concepts
Understanding the calculation of 26 out of 45 as a percentage opens doors to exploring related concepts:
-
Proportions: The relationship between 26 and 45 can be expressed as a proportion: 26/45 = x/100. Solving for 'x' provides the percentage.
-
Ratios: The ratio of 26 to 45 (26:45) expresses the relative size of one quantity compared to another. This ratio simplifies to approximately 0.58:1.
-
Fractions: As shown above, the initial representation (26/45) is a fraction. Understanding fraction simplification and conversion to decimals and percentages is essential.
-
Statistical Significance: In larger datasets, the significance of a percentage like 57.78% needs to be evaluated using statistical methods. This is vital in research and surveys.
Common Misconceptions about Percentages
Several common misconceptions surround percentages:
-
Adding Percentages Directly: You cannot simply add percentages directly unless they are from the same base. For example, a 10% increase followed by a 10% decrease does not result in a net change of 0%.
-
Misinterpreting Percentage Changes: A percentage change is relative to the original value. A 50% increase from 10 is 15, but a 50% decrease from 15 back to 10 is not the same relative change.
-
Ignoring the Base: Always consider the base value (the total or "whole") when interpreting percentages. A small percentage of a large number can be more significant than a large percentage of a small number.
Practical Applications and Real-World Examples
Percentages are used extensively in various real-world scenarios:
-
Finance: Calculating interest rates, discounts, taxes, and profit margins.
-
Science: Representing experimental results, statistical probabilities, and error margins.
-
Retail: Determining discounts, sales tax, and profit margins.
-
Healthcare: Tracking disease prevalence, success rates of treatments, and patient demographics.
-
Education: Assessing student performance, evaluating program effectiveness, and measuring participation rates.
Frequently Asked Questions (FAQs)
-
Q: How do I calculate a percentage increase or decrease?
A: To calculate a percentage increase, subtract the original value from the new value, divide the result by the original value, and multiply by 100. For a percentage decrease, follow the same steps but express the result as a negative value.
-
Q: What if I need to calculate a percentage of a percentage?
A: Convert both percentages to decimals and then multiply them together. Finally, multiply the result by 100 to express the answer as a percentage.
-
Q: How can I improve my understanding of percentages?
A: Practice regularly with various problems. Use online resources, calculators, and educational materials to reinforce your understanding.
Conclusion: Mastering Percentages for Success
Understanding percentages is a critical skill for navigating various aspects of life. This article demonstrates the calculation and interpretation of 26 out of 45 as approximately 57.78%, emphasizing the importance of context in understanding the meaning of this value. By grasping the fundamentals of percentage calculations and avoiding common misconceptions, you'll be well-equipped to apply this valuable skill in various academic, professional, and personal contexts. Remember that the power of percentages lies not just in the calculation, but in the meaningful insights it provides when applied to real-world situations. Continue practicing and exploring diverse applications of percentages to truly master this fundamental concept.
Latest Posts
Latest Posts
-
Baking Soda Vs Bicarb Soda
Sep 16, 2025
-
What Is Suspense In Accounting
Sep 16, 2025
-
What Fruit Starts With K
Sep 16, 2025
-
Body Parts Beginning With H
Sep 16, 2025
-
What Fruit Starts With Z
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 26 Out Of 45 Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.