26 30 As A Percentage
candidatos
Sep 20, 2025 · 5 min read
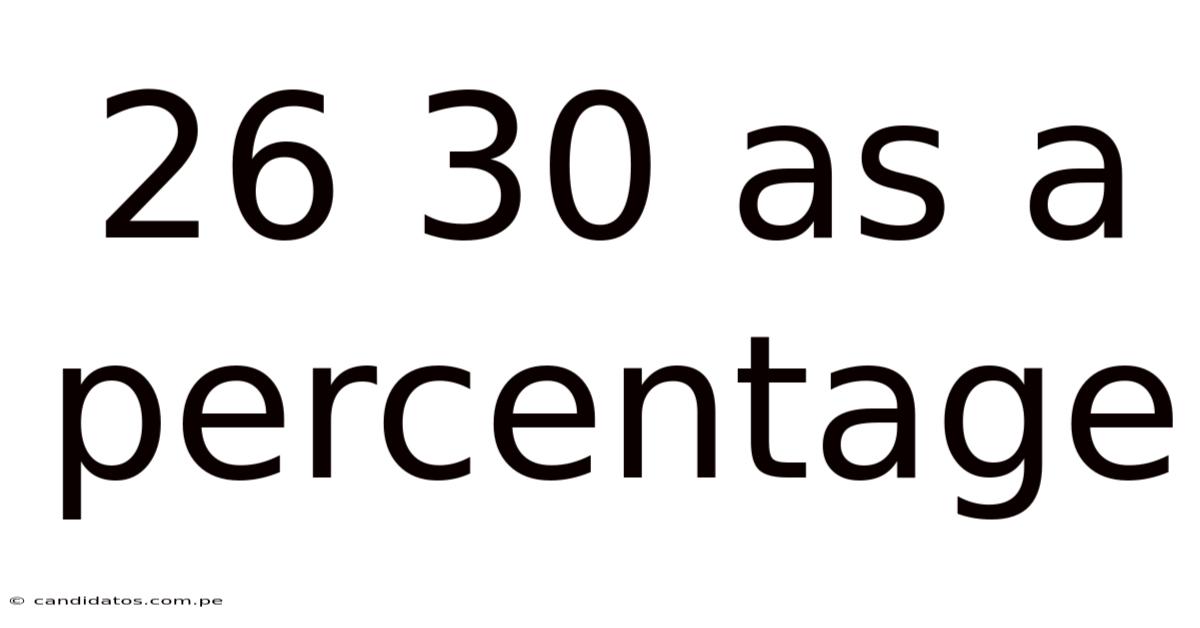
Table of Contents
Decoding 26 out of 30: A Comprehensive Guide to Percentage Calculations and Interpretations
Understanding percentages is a fundamental skill applicable across various fields, from academic assessments to financial analysis. This article delves deep into calculating and interpreting the percentage represented by 26 out of 30, offering a comprehensive understanding beyond a simple numerical answer. We'll explore the calculation process, discuss its practical applications, and address common misunderstandings surrounding percentage calculations. This guide is designed for anyone looking to grasp the nuances of percentage calculations and apply them effectively.
Understanding the Fundamentals: What is a Percentage?
A percentage is a fraction or ratio expressed as a number out of 100. It represents a proportion of a whole. The symbol "%" signifies "per hundred," indicating the part relative to the total. For instance, 50% means 50 out of 100, or one-half. Understanding this basic principle is crucial for correctly calculating and interpreting percentages.
Calculating 26 out of 30 as a Percentage: A Step-by-Step Guide
The calculation of 26 out of 30 as a percentage involves a straightforward process:
-
Formulate the Fraction: Express the given numbers as a fraction. In this case, it's 26/30. This fraction represents the proportion of 26 relative to the total of 30.
-
Convert the Fraction to a Decimal: Divide the numerator (26) by the denominator (30). This gives you a decimal value: 26 ÷ 30 = 0.866666... We can round this to a manageable number of decimal places, such as 0.867.
-
Convert the Decimal to a Percentage: Multiply the decimal value by 100. This converts the decimal representation to a percentage: 0.867 x 100 = 86.7%.
Therefore, 26 out of 30 is 86.7%.
Interpreting the Result: What Does 86.7% Mean?
The calculated 86.7% signifies that 26 represents 86.7% of the total value of 30. This implies a high proportion; a significant portion of the total is represented by 26. The interpretation will vary depending on the context.
For example:
- Academic Performance: If 26 represents the number of correct answers out of 30 questions on a test, an 86.7% score indicates a strong performance.
- Sales Targets: If 26 represents the number of units sold out of a target of 30, 86.7% indicates near achievement of the sales goal.
- Project Completion: If 26 tasks are completed out of a total of 30 tasks in a project, 86.7% shows significant progress towards completion.
The meaning and significance of 86.7% are entirely dependent on the context in which it is used.
Expanding the Understanding: Practical Applications of Percentage Calculations
Percentage calculations are ubiquitous in various aspects of daily life and professional fields. Here are a few examples:
- Finance: Calculating interest rates, discounts, profit margins, and tax rates all involve percentage calculations. Understanding percentages is essential for making informed financial decisions.
- Statistics: Percentages are used to represent proportions and probabilities in data analysis and interpretation. They are crucial for understanding trends and making predictions.
- Science: Percentage changes are frequently used to express variations in experimental results and data analysis.
- Education: Grades, test scores, and performance metrics are often expressed as percentages.
- Retail: Sales discounts, markups, and profit margins are expressed as percentages to attract customers and manage inventory efficiently.
Beyond the Basics: Advanced Percentage Calculations
While calculating 26 out of 30 as a percentage is straightforward, understanding more complex scenarios is beneficial. Let's consider some advanced aspects:
-
Percentage Increase/Decrease: Calculating the percentage increase or decrease between two values involves finding the difference between the two values, dividing this difference by the original value, and multiplying by 100.
-
Percentage of a Percentage: This involves calculating a percentage of an already existing percentage. For example, finding 10% of 86.7% would involve multiplying 0.867 by 0.1, resulting in 8.67%.
-
Reverse Percentage Calculations: This involves finding the original value when given a percentage and the resulting value. For instance, if 86.7% of a number is 26, then the original number can be calculated by dividing 26 by 0.867.
Mastering these advanced calculations expands the practical applicability of percentage understanding.
Addressing Common Misconceptions: Avoiding Percentage Pitfalls
Several common misconceptions can lead to incorrect percentage calculations. Let's clarify these potential pitfalls:
-
Confusing Percentage with Absolute Values: A percentage represents a proportion, not an absolute value. A 10% increase in a large quantity is significantly larger than a 10% increase in a small quantity.
-
Incorrect Rounding: Rounding decimals during intermediate steps of calculation can lead to inaccuracies in the final result. It’s generally best to maintain precision until the final answer.
-
Misinterpreting Percentage Change: The percentage change between two values depends on which value is used as the base. Understanding the context is crucial for accurate interpretation.
Frequently Asked Questions (FAQ)
Q: What is the formula for calculating percentages?
A: The basic formula is: (Part / Whole) x 100 = Percentage
Q: How do I calculate a percentage increase?
A: (New Value - Original Value) / Original Value) x 100 = Percentage Increase
Q: How do I calculate a percentage decrease?
A: (Original Value - New Value) / Original Value) x 100 = Percentage Decrease
Q: Can I use a calculator to find percentages?
A: Yes, most calculators have a percentage function that simplifies these calculations. Alternatively, you can perform the calculations manually using the formulas.
Conclusion: Mastering the Art of Percentage Calculations
Understanding percentage calculations is a valuable life skill. This article provided a detailed explanation of calculating 26 out of 30 as a percentage (86.7%), along with a comprehensive exploration of the underlying principles, practical applications, and potential pitfalls. By mastering these concepts and avoiding common mistakes, you can confidently tackle percentage-related problems in various contexts, from academic pursuits to professional endeavors. Remember that the key lies not just in the calculation itself but also in the insightful interpretation of the results within their specific context.
Latest Posts
Latest Posts
-
Birds That Start With S
Sep 20, 2025
-
225 Degrees F In C
Sep 20, 2025
-
Rarest Fruit In The World
Sep 20, 2025
-
Adjectives For The Letter L
Sep 20, 2025
-
Liquefied Petroleum Gas Vs Propane
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 26 30 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.