25 Squared - 7 Squared
candidatos
Sep 20, 2025 · 6 min read
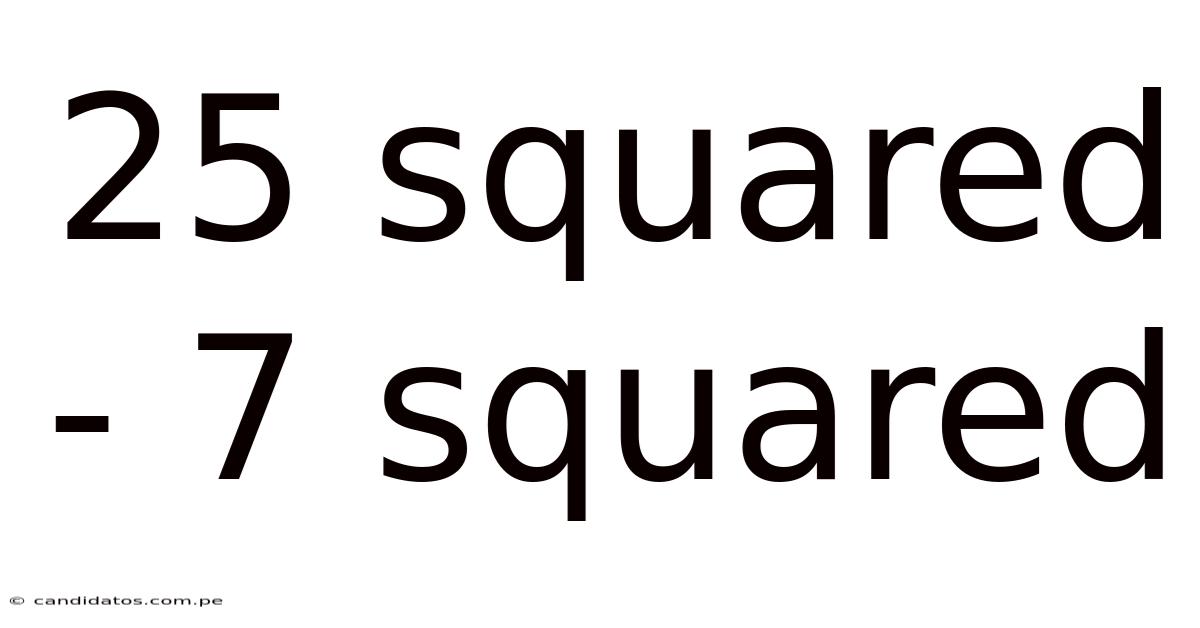
Table of Contents
Unveiling the Mystery: A Deep Dive into 25 Squared Minus 7 Squared
This article explores the seemingly simple mathematical expression "25 squared minus 7 squared," delving far beyond the basic calculation to uncover underlying mathematical principles, explore practical applications, and connect this seemingly isolated problem to broader mathematical concepts. We'll unravel the mystery, not just providing the answer, but equipping you with a deeper understanding of squares, differences of squares, and their significance in various fields. This exploration is perfect for anyone from high school students brushing up on their algebra to adults seeking to refresh their mathematical knowledge. Understanding this concept opens doors to more advanced mathematical concepts and their real-world applications.
Understanding Squares and the Difference of Squares
Before diving into the calculation of 25² - 7², let's solidify our understanding of the fundamental concepts involved.
-
Squares: A square of a number is simply that number multiplied by itself. For example, 5 squared (written as 5²) is 5 * 5 = 25. The square of a number represents the area of a square with sides of that length.
-
Difference of Squares: This is a specific algebraic expression in the form a² - b², where 'a' and 'b' are any numbers or variables. It's called a "difference" because it involves subtraction, and "of squares" because both terms are squares. The difference of squares has a very useful factorization: a² - b² = (a + b)(a - b). This factorization is a crucial tool in many algebraic manipulations and problem-solving techniques.
Calculating 25 Squared Minus 7 Squared: The Direct Approach
The most straightforward approach to solving 25² - 7² is to calculate each square individually and then subtract:
- Calculate 25²: 25 * 25 = 625
- Calculate 7²: 7 * 7 = 49
- Subtract: 625 - 49 = 576
Therefore, 25² - 7² = 576. This method is simple and effective for smaller numbers, but it becomes cumbersome with larger numbers or when dealing with variables.
Calculating 25 Squared Minus 7 Squared: Using the Difference of Squares Formula
This is where the elegance and power of the difference of squares factorization shines. Recognizing that 25² - 7² is in the form a² - b², we can directly apply the formula:
a² - b² = (a + b)(a - b)
In our case, a = 25 and b = 7. Therefore:
25² - 7² = (25 + 7)(25 - 7) = (32)(18)
Now, we can easily multiply 32 and 18:
32 * 18 = 576
This method provides the same result (576) as the direct approach but demonstrates a more efficient and conceptually richer approach, especially useful for more complex problems.
Applications of the Difference of Squares: Beyond Simple Calculations
The difference of squares formula is far from a mere mathematical curiosity; it has significant applications in various fields:
-
Algebraic Simplification: The formula simplifies complex algebraic expressions, making them easier to manipulate and solve equations. Consider expressions like (x² - 16). Using the difference of squares, we can factor it as (x + 4)(x - 4), which is much simpler to work with.
-
Solving Quadratic Equations: The difference of squares is often a key step in solving quadratic equations, particularly those that can be factored.
-
Geometry and Area Calculations: Remember that a square of a number represents the area of a square. The difference of squares can represent the difference in areas between two squares. This concept finds application in various geometric problems involving area calculations.
-
Calculus: The difference of squares forms the basis for various techniques in calculus, particularly when dealing with limits and derivatives.
-
Number Theory: The difference of squares plays a role in number theory, specifically in exploring perfect squares and their properties. Understanding the difference of squares helps analyze the structure of numbers and their relationships.
-
Physics and Engineering: Many physical phenomena and engineering designs involve relationships that can be represented using quadratic equations. The ability to factor quadratic equations using the difference of squares is essential for solving various engineering and physics problems. For example, in projectile motion, the difference in squares can simplify calculations related to the vertical component of displacement.
-
Computer Science: The concept is essential in algorithm design and optimization. Many algorithms rely on efficient mathematical operations, and the difference of squares provides a faster way to compute certain values. For example, cryptographic algorithms utilize efficient number theory, and concepts like the difference of squares can contribute to the design of optimized security systems.
Extending the Concept: Beyond 25 and 7
The principles explored with 25² - 7² apply equally to any numbers or variables. Consider these examples:
-
100² - 25²: Using the difference of squares formula: (100 + 25)(100 - 25) = (125)(75) = 9375
-
x² - y²: This remains as (x + y)(x - y). The formula holds true for any variables 'x' and 'y'.
-
(a + b)² - c²: This can be expanded using the formula, but it first requires expanding (a + b)². The result would then be factored using difference of squares. This shows the power of this concept in simplifying even more complex scenarios.
Frequently Asked Questions (FAQs)
Q: Is there any other way to calculate 25² - 7² without using the difference of squares formula?
A: Yes, you can use the direct method of calculating each square individually and then subtracting. However, the difference of squares method is generally more efficient and reveals the underlying mathematical structure more clearly.
Q: What if the expression was 7² - 25²?
A: In this case, we would have a negative result. The difference of squares formula would still apply: (7 + 25)(7 - 25) = (32)(-18) = -576. This highlights the importance of paying attention to the order of subtraction.
Q: Are there any limitations to the difference of squares formula?
A: The formula applies only to expressions that are in the form a² - b². It cannot be directly applied to expressions like a² + b² or a³ - b³. However, other factorization techniques exist for handling these types of expressions.
Q: How can I practice applying the difference of squares formula?
A: Practice with various examples. Start with simple numbers and gradually increase the complexity. You can also create your own problems to challenge yourself. Working through various examples helps solidify your understanding. Consider working with problems that involve variables to deepen your grasp of the application within broader algebraic contexts.
Conclusion: More Than Just a Calculation
This deep dive into "25 squared minus 7 squared" reveals that this simple-looking mathematical problem opens doors to a wider understanding of fundamental algebraic concepts and their significant implications. The difference of squares formula is a powerful tool, simplifying complex expressions, solving equations, and finding applications in various fields, ranging from basic geometry and algebra to advanced physics and computer science. Mastering this concept builds a solid foundation for tackling more advanced mathematical challenges and highlights the elegance and interconnectedness of mathematical principles. The journey beyond the simple calculation of 576 showcases the richness and practicality of mathematical concepts often underestimated in their initial presentation.
Latest Posts
Latest Posts
-
Pictures Of A Rock Cycle
Sep 20, 2025
-
Lithium Element Protons Neutrons Electrons
Sep 20, 2025
-
Desire Crossword Clue 4 Letters
Sep 20, 2025
-
Do Other Animals Get Pimples
Sep 20, 2025
-
Animal Name With Letter E
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 25 Squared - 7 Squared . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.