25 50 As A Percent
candidatos
Sep 23, 2025 · 5 min read
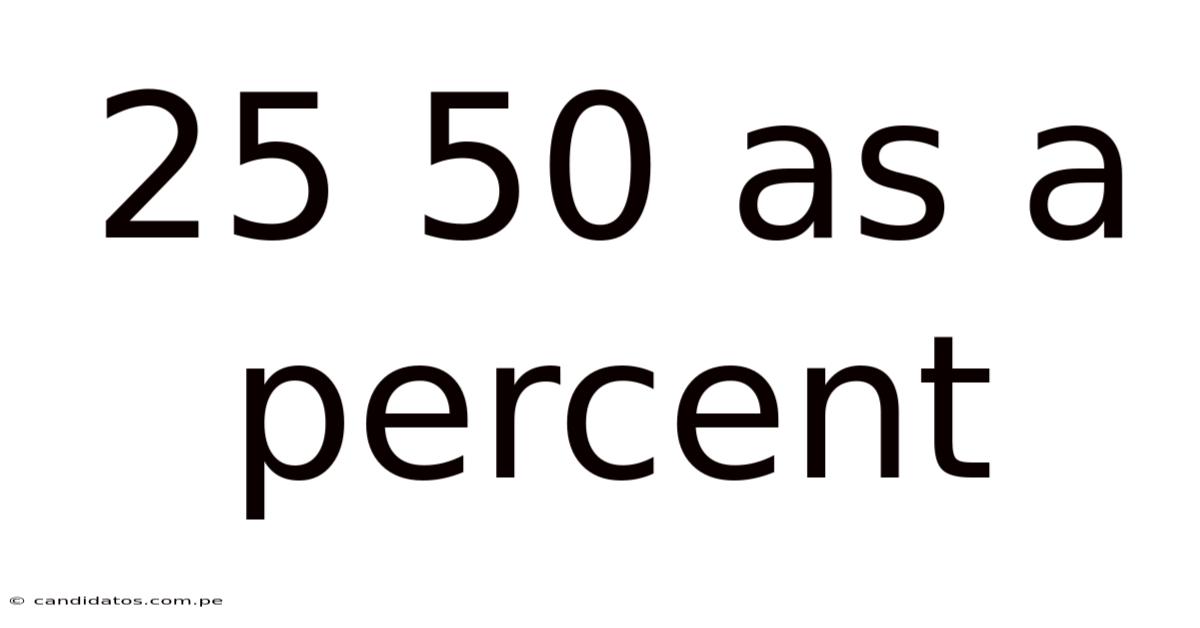
Table of Contents
25 of 50 as a Percent: Understanding Percentages and Their Applications
Understanding percentages is a fundamental skill in mathematics with widespread applications in everyday life, from calculating discounts and taxes to analyzing data and understanding financial reports. This article will delve into how to calculate "25 of 50 as a percent," explaining the process step-by-step and exploring various methods. We'll also examine the broader context of percentage calculations, offering practical examples and addressing frequently asked questions. This comprehensive guide aims to equip you with a solid grasp of percentages and their relevance in various situations.
Understanding Percentages: A Quick Refresher
A percentage is a way of expressing a number as a fraction of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of a hundred." Therefore, a percentage represents a proportion or ratio out of 100. For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5 as a decimal.
Calculating percentages involves understanding the relationship between the part, the whole, and the percentage itself. The formula is:
(Part / Whole) * 100% = Percentage
Calculating 25 of 50 as a Percentage: Step-by-Step Guide
Let's apply this to our specific question: "What is 25 of 50 as a percentage?"
1. Identify the Part and the Whole:
- Part: This is the number we're considering as a portion of the whole – in this case, 25.
- Whole: This is the total amount that the part is a fraction of – in this case, 50.
2. Apply the Percentage Formula:
Using the formula above, we substitute the values:
(25 / 50) * 100% = Percentage
3. Perform the Calculation:
- First, divide the part by the whole: 25 / 50 = 0.5
- Then, multiply the result by 100%: 0.5 * 100% = 50%
Therefore, 25 out of 50 is 50%.
Alternative Methods for Calculating Percentages
While the above method is straightforward, there are alternative approaches that can be useful depending on the context and your comfort level with mathematical operations:
-
Using Proportions: You can set up a proportion to solve for the percentage. For example:
25/50 = x/100
Cross-multiplying gives: 50x = 2500
Solving for x: x = 2500 / 50 = 50
Therefore, x = 50%, demonstrating the same result.
-
Mental Math: For simpler percentages, mental math can be quicker. Recognizing that 25 is half of 50 allows for immediate calculation: half as a percentage is 50%. This approach is valuable for quick estimations.
-
Using a Calculator: Calculators are especially helpful for more complex percentage calculations. Simply input (25/50)*100 to arrive at the answer, 50%.
Practical Applications of Percentage Calculations
Understanding percentage calculations is essential in various real-world situations, including:
-
Financial Calculations: Calculating interest rates, discounts, taxes, tips, profit margins, and investment returns all heavily rely on percentage calculations. For instance, a 10% discount on a $100 item means a saving of $10 (10% of $100).
-
Data Analysis: Percentages are used extensively to represent data in charts, graphs, and reports. For example, the percentage of students who passed an exam, or the market share of a particular company, are expressed as percentages to provide a clear and concise representation.
-
Scientific Studies: In scientific research, percentages are frequently used to present results and draw conclusions. For example, the success rate of a particular medical treatment or the percentage of participants exhibiting a specific trait in a study are expressed as percentages.
-
Everyday Life: Determining sales tax, calculating the percentage of ingredients in a recipe, or figuring out the tip at a restaurant involves percentage calculations.
Beyond the Basics: Working with More Complex Percentages
While "25 of 50 as a percent" presents a relatively simple calculation, understanding percentages extends to more complex scenarios:
-
Calculating Percentage Increase or Decrease: This involves determining the percentage change between two numbers. For example, if a price increases from $50 to $60, the percentage increase is calculated as:
[(60 - 50) / 50] * 100% = 20%
-
Finding the Original Value: If you know the percentage and the final value after a percentage increase or decrease, you can work backward to find the original value. This often requires setting up an algebraic equation.
-
Compounding Percentages: This deals with situations where percentages are applied repeatedly. For instance, compound interest calculations in finance involve applying interest rates to an accumulating balance over time.
Frequently Asked Questions (FAQs)
Q1: What if the "part" is larger than the "whole"?
If the part is larger than the whole, the resulting percentage will be greater than 100%. This indicates that the part exceeds the whole, which can happen in certain contexts (e.g., growth percentages exceeding 100%).
Q2: How do I convert a decimal to a percentage?
To convert a decimal to a percentage, multiply the decimal by 100 and add the "%" symbol. For example, 0.75 becomes 75%.
Q3: How do I convert a fraction to a percentage?
To convert a fraction to a percentage, divide the numerator by the denominator and multiply the result by 100%. For example, 3/4 becomes (3/4) * 100% = 75%.
Q4: Are there any online tools or calculators for percentage calculations?
Yes, many online calculators and tools are available for performing various percentage calculations, simplifying the process. However, understanding the underlying principles is crucial for effective problem-solving.
Q5: Why is understanding percentages important?
Understanding percentages is crucial for making informed decisions in various aspects of life, from personal finance to professional endeavors, by enabling the interpretation and application of numerical data efficiently.
Conclusion: Mastering the Art of Percentages
Understanding how to calculate "25 of 50 as a percent," and percentages in general, is a valuable mathematical skill with countless real-world applications. From simple calculations to more complex scenarios involving percentage increases, decreases, and compounding, mastering this fundamental concept empowers you to navigate various quantitative challenges with confidence and accuracy. By applying the straightforward formula and understanding the underlying principles, you can confidently tackle percentage problems and use this knowledge to make informed decisions in your daily life. Remember that consistent practice and a firm grasp of the underlying concepts are key to mastering this essential mathematical skill.
Latest Posts
Latest Posts
-
Modulus Of Elasticity In Steel
Sep 24, 2025
-
How To Pronounce The Maldives
Sep 24, 2025
-
Ascorbic Acid Vs Citric Acid
Sep 24, 2025
-
Diagram Of Male Human Body
Sep 24, 2025
-
Liquid Solid And Gas Diagram
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 25 50 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.