23 25 As A Percent
candidatos
Sep 22, 2025 · 5 min read
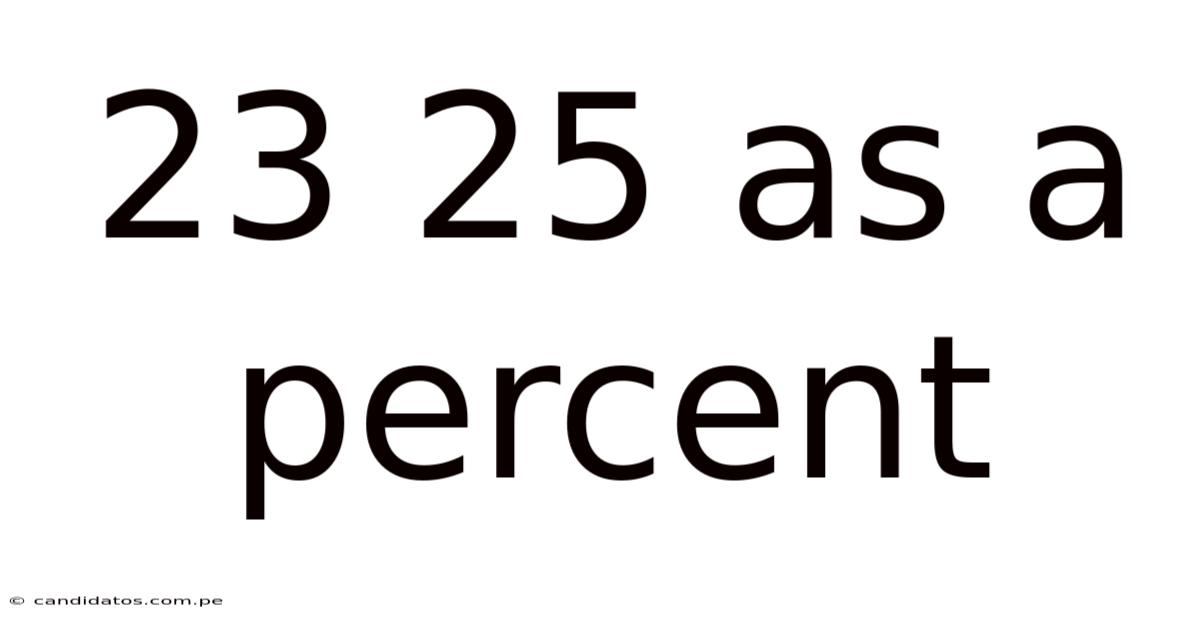
Table of Contents
Understanding 23/25 as a Percentage: A Comprehensive Guide
Calculating percentages is a fundamental skill applicable across numerous fields, from everyday budgeting to complex scientific analyses. This article will provide a comprehensive guide on how to calculate 23/25 as a percentage, explaining the underlying principles and offering various methods to solve this and similar problems. We'll delve into the theoretical background, explore practical applications, and address frequently asked questions. By the end, you'll not only know the answer but also understand the process deeply, empowering you to tackle any percentage calculation with confidence.
Introduction: Percentages and Their Significance
A percentage is a way of expressing a number as a fraction of 100. It represents a proportion or ratio out of a whole. The symbol "%" signifies "per cent," meaning "out of one hundred." Percentages are ubiquitous in our daily lives, used to express discounts, interest rates, tax rates, statistical data, and much more. Understanding percentages is crucial for informed decision-making in various contexts.
The core concept involves relating a part to a whole. For instance, if you score 23 out of 25 on a test, you've achieved a certain percentage of the total possible marks. This article focuses on precisely that – calculating the percentage represented by the fraction 23/25.
Method 1: The Direct Conversion Method
The most straightforward approach to convert a fraction to a percentage involves two simple steps:
-
Convert the fraction to a decimal: Divide the numerator (the top number) by the denominator (the bottom number). In this case, we divide 23 by 25:
23 ÷ 25 = 0.92
-
Convert the decimal to a percentage: Multiply the decimal by 100 and add the "%" symbol.
0.92 x 100 = 92%
Therefore, 23/25 is equal to 92%.
Method 2: Using Proportions
This method is particularly useful for understanding the underlying relationship between the fraction and the percentage. We set up a proportion:
- Fraction: 23/25
- Percentage: x/100 (where 'x' represents the unknown percentage)
We then solve for 'x' by cross-multiplying:
23/25 = x/100
23 * 100 = 25 * x
2300 = 25x
x = 2300 / 25
x = 92
Therefore, x = 92%, confirming our previous result. This method emphasizes the equivalence between the fraction and the percentage, highlighting that they represent the same proportion.
Method 3: Applying Percentage Formula Directly
The fundamental formula for calculating a percentage is:
(Part / Whole) * 100% = Percentage
In our case:
(23 / 25) * 100% = 92%
This formula directly incorporates the fraction into the percentage calculation, providing a concise and efficient way to determine the percentage.
Practical Applications of Percentage Calculations
The ability to convert fractions to percentages has wide-ranging applications:
-
Academic Performance: Calculating grades, test scores, and overall academic progress. A score of 23 out of 25 on a quiz represents a strong performance of 92%.
-
Financial Matters: Determining discounts, interest rates, profit margins, tax calculations, and investment returns. Understanding percentages is critical for making informed financial decisions.
-
Data Analysis: Representing and interpreting statistical data, such as survey results, market share, and population demographics. Percentages allow for easy comparison and visualization of data.
-
Science and Engineering: Expressing experimental results, measurement errors, and efficiency ratios. Accurate percentage calculations are vital for maintaining precision in scientific and engineering projects.
-
Everyday Life: Calculating tips at restaurants, understanding sales discounts, and comparing prices of different products. Percentages are an integral part of everyday decision-making.
Beyond the Basics: Working with Different Fractions
While this article focused on 23/25, the methods described are applicable to any fraction. Let's explore a few examples:
-
15/20: 15 ÷ 20 = 0.75 => 0.75 * 100% = 75%
-
7/10: 7 ÷ 10 = 0.7 => 0.7 * 100% = 70%
-
3/4: 3 ÷ 4 = 0.75 => 0.75 * 100% = 75%
By consistently applying these methods, you can efficiently convert any fraction into its percentage equivalent.
Understanding Decimal Places and Rounding
In some cases, the decimal resulting from the division might have more than two decimal places. For example, if the fraction was 23/27, the decimal would be approximately 0.85185. When converting to a percentage, you may need to round the number. Common rounding practices include:
- Rounding to the nearest whole number: 0.85185 rounded to the nearest whole number is 0.85, resulting in 85%.
- Rounding to one decimal place: 0.85185 rounded to one decimal place is 0.9, resulting in 90%.
- Rounding to two decimal places: 0.85185 rounded to two decimal places is 0.85, resulting in 85%.
The level of precision required depends on the context of the calculation. For many applications, rounding to one or two decimal places is sufficient.
Frequently Asked Questions (FAQ)
Q1: What if the denominator is zero?
A1: Division by zero is undefined in mathematics. You cannot calculate a percentage if the denominator (the whole) is zero.
Q2: Can I convert a percentage back into a fraction?
A2: Yes, absolutely! To convert a percentage to a fraction, divide the percentage by 100 and simplify the resulting fraction. For example, 92% becomes 92/100, which simplifies to 23/25.
Q3: How do I handle very large or very small fractions?
A3: The methods remain the same. Use a calculator or software for larger numbers to ensure accuracy. For extremely small fractions, you might need to express the percentage with more decimal places to capture the precision needed.
Q4: Are there any online calculators to verify my results?
A4: Yes, many online calculators are available that can perform fraction-to-percentage conversions. These can be useful for double-checking your manual calculations.
Conclusion: Mastering Percentage Calculations
Converting fractions to percentages is a fundamental mathematical skill with widespread applications. This comprehensive guide has explored three different methods for calculating 23/25 as a percentage, demonstrating that the answer is 92%. Beyond the specific example, the principles outlined here empower you to tackle any fraction-to-percentage conversion with confidence. Remember the core concepts, practice the methods, and you will master this essential skill for academic, professional, and personal success. Understanding percentages is not just about knowing the formulas; it's about grasping the underlying principles and their relevance to the world around us.
Latest Posts
Latest Posts
-
Port On The Arabian Sea
Sep 22, 2025
-
Probability From Two Way Tables
Sep 22, 2025
-
1 27 As A Percent
Sep 22, 2025
-
Hope Gets Naughty In Class
Sep 22, 2025
-
Does Freezing Food Kill Germs
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 23 25 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.