21 56 In Simplest Form
candidatos
Sep 17, 2025 · 5 min read
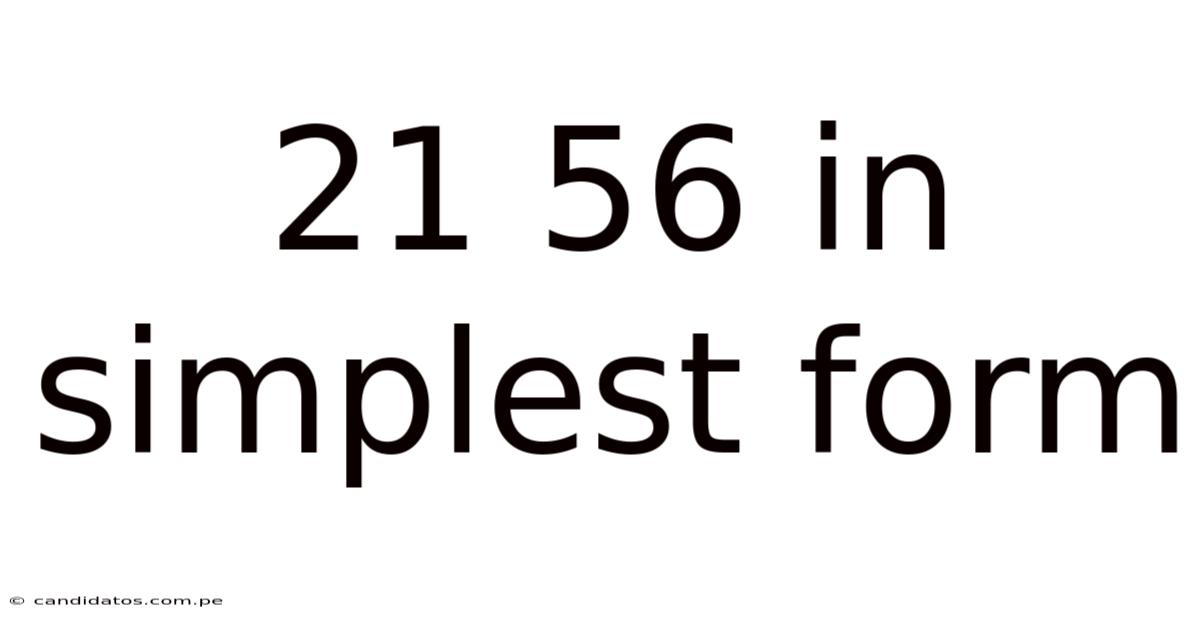
Table of Contents
Simplifying Fractions: A Deep Dive into 21/56
Understanding fractions is a fundamental concept in mathematics, crucial for various applications in everyday life and advanced studies. This article will explore the simplification of the fraction 21/56, providing a step-by-step guide and delving into the underlying mathematical principles. We will cover the process, explain the reasoning behind it, and address frequently asked questions. By the end, you will not only know the simplest form of 21/56 but also grasp the broader concept of fraction reduction.
Introduction: What is Fraction Simplification?
Simplifying a fraction, also known as reducing a fraction to its simplest form or expressing a fraction in lowest terms, means finding an equivalent fraction where the numerator and denominator have no common factors other than 1. This process makes the fraction easier to understand and work with in calculations. It essentially represents the same proportion or value in a more concise and efficient manner. The fraction 21/56, while perfectly valid, can be simplified to a smaller, equivalent fraction.
Steps to Simplify 21/56
The simplification process involves finding the greatest common divisor (GCD) or highest common factor (HCF) of the numerator (21) and the denominator (56). The GCD is the largest number that divides both the numerator and denominator without leaving a remainder. Here’s a step-by-step breakdown:
-
Find the factors of the numerator (21): The factors of 21 are 1, 3, 7, and 21. These are the numbers that divide 21 evenly.
-
Find the factors of the denominator (56): The factors of 56 are 1, 2, 4, 7, 8, 14, 28, and 56.
-
Identify the greatest common factor (GCF): Comparing the lists of factors, we see that the largest number that appears in both lists is 7. Therefore, the GCF of 21 and 56 is 7.
-
Divide both the numerator and denominator by the GCF: Divide both 21 and 56 by 7:
- 21 ÷ 7 = 3
- 56 ÷ 7 = 8
-
The simplified fraction: The simplified form of 21/56 is therefore 3/8.
Understanding the Mathematical Principles
The process of simplifying fractions relies on the fundamental principle of equivalent fractions. Two fractions are equivalent if they represent the same proportion or value. We can obtain an equivalent fraction by multiplying or dividing both the numerator and denominator by the same non-zero number.
In our case, we divided both 21 and 56 by their GCF, 7. This operation doesn't change the value of the fraction; it simply expresses it in a more concise form. Think of it like this: Imagine you have a pizza cut into 56 slices. If you take 21 slices, you have 21/56 of the pizza. Now imagine that you group the slices into sets of 7. You now have 3 sets of 7 slices out of 8 sets of 7 slices, which is 3/8 of the pizza. The amount of pizza remains the same; only the representation has changed.
Alternative Methods for Finding the GCF
While listing factors works well for smaller numbers, it can become cumbersome for larger numbers. Here are two alternative methods for finding the GCF:
-
Prime Factorization: This method involves breaking down the numerator and denominator into their prime factors. The GCF is the product of the common prime factors raised to the lowest power.
- Prime factorization of 21: 3 x 7
- Prime factorization of 56: 2 x 2 x 2 x 7 = 2³ x 7
The only common prime factor is 7. Therefore, the GCF is 7.
-
Euclidean Algorithm: This is a more efficient method for finding the GCF of larger numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCF.
- Divide 56 by 21: 56 = 2 x 21 + 14
- Divide 21 by the remainder 14: 21 = 1 x 14 + 7
- Divide 14 by the remainder 7: 14 = 2 x 7 + 0
The last non-zero remainder is 7, which is the GCF.
Applications of Fraction Simplification
Simplifying fractions is essential in various mathematical contexts:
-
Arithmetic Operations: Simplifying fractions before performing addition, subtraction, multiplication, or division makes calculations easier and less prone to errors.
-
Algebra: Simplifying fractions is crucial in manipulating algebraic expressions and solving equations.
-
Geometry: Many geometric problems involve fractions, and simplifying them makes it easier to interpret the results.
-
Real-world problems: Fractions are used to represent parts of wholes in numerous real-world situations, such as measuring ingredients in cooking, calculating proportions in construction, or expressing probabilities in statistics. Simplifying these fractions provides a clearer and more efficient representation.
Frequently Asked Questions (FAQ)
-
Q: Is 3/8 the only simplified form of 21/56?
- A: Yes, 3/8 is the simplest form because the numerator (3) and denominator (8) have no common factors other than 1.
-
Q: What happens if I divide the numerator and denominator by a number that is not the GCF?
- A: You will obtain an equivalent fraction, but it won't be in its simplest form. You'll need to repeat the simplification process until you reach the fraction with the GCF. For example, if you divide 21/56 by 3, you get 7/18.66... which still needs further simplification.
-
Q: Can I simplify a fraction that has a numerator greater than its denominator (an improper fraction)?
- A: Yes, you can simplify improper fractions using the same method. For instance, the improper fraction 28/21 can be simplified to 4/3 by dividing both numerator and denominator by their GCF, 7.
-
Q: What if the GCF is 1?
- A: If the GCF of the numerator and denominator is 1, then the fraction is already in its simplest form. It cannot be further simplified.
Conclusion: Mastering Fraction Simplification
Simplifying fractions is a fundamental skill in mathematics, and mastering this process is essential for success in various mathematical and real-world applications. We’ve explored several methods to simplify fractions, focusing on the fraction 21/56 and illustrating the underlying mathematical principles. Remember, the goal is to find the greatest common factor of the numerator and denominator and then divide both by this factor. By understanding these concepts and practicing regularly, you will build confidence and proficiency in working with fractions. The journey from 21/56 to its simplest form, 3/8, demonstrates the power and elegance of this fundamental mathematical operation. Understanding this not only helps with solving problems but also builds a crucial foundation for more complex mathematical concepts in the future.
Latest Posts
Latest Posts
-
Words That Start With Ke
Sep 17, 2025
-
I Can Smell Your Nappy
Sep 17, 2025
-
Chemical Formula For Lithium Fluoride
Sep 17, 2025
-
Calculator For Coefficient Of Variation
Sep 17, 2025
-
Musical Instruments In A Band
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 21 56 In Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.