20 Percent Of 500 000
candidatos
Sep 22, 2025 · 5 min read
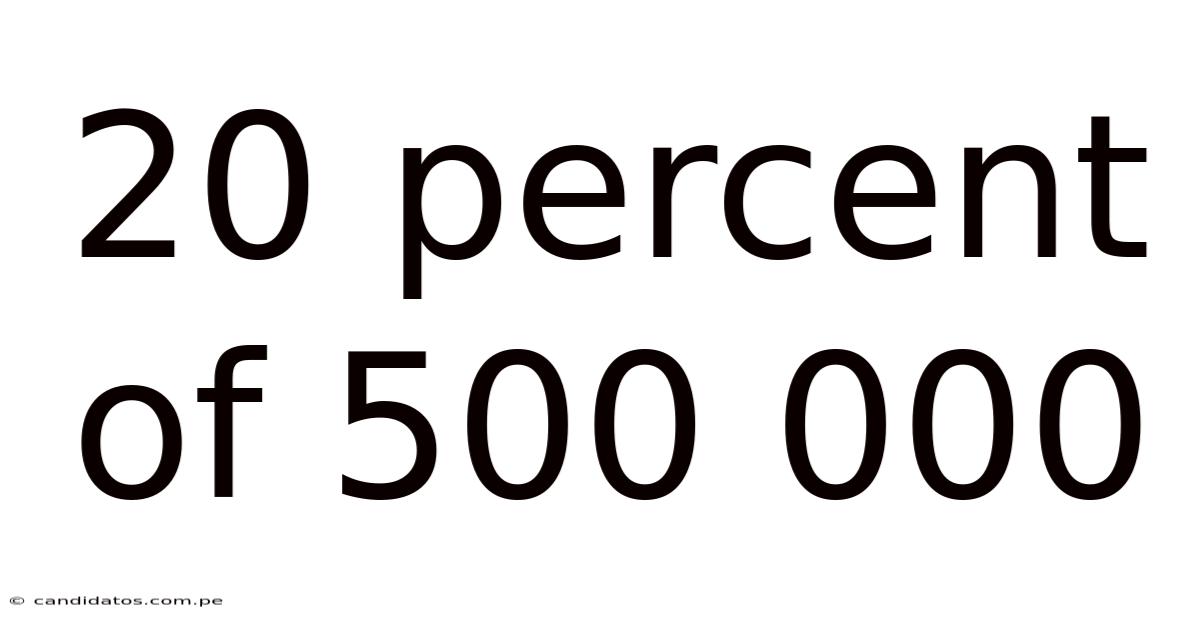
Table of Contents
Decoding 20% of 500,000: A Deep Dive into Percentages and Their Applications
Finding 20% of 500,000 might seem like a simple arithmetic problem, easily solvable with a calculator. However, understanding the underlying principles of percentages and their diverse applications extends far beyond a single calculation. This article delves into the intricacies of percentage calculations, explores different methods to solve this specific problem, and expands on the significance of percentages in various fields, from finance and statistics to everyday life. We'll even tackle some common misconceptions and provide you with the tools to confidently tackle similar percentage problems in the future.
Understanding Percentages: The Foundation
A percentage is simply a fraction expressed as a part of 100. The word "percent" literally means "out of one hundred" ( per centum in Latin). Therefore, 20% represents 20 parts out of 100, or the fraction 20/100, which simplifies to 1/5. This fundamental understanding allows us to approach percentage calculations in several ways.
Method 1: Direct Calculation using Decimal Conversion
The most straightforward method involves converting the percentage to a decimal and then multiplying it by the total value. To find 20% of 500,000:
- Convert the percentage to a decimal: 20% is equal to 20/100 = 0.20.
- Multiply the decimal by the total value: 0.20 * 500,000 = 100,000
Therefore, 20% of 500,000 is 100,000.
Method 2: Fractional Approach
As mentioned earlier, 20% is equivalent to the fraction 1/5. This allows us to solve the problem using division:
- Express the percentage as a fraction: 20% = 1/5
- Divide the total value by the denominator of the fraction: 500,000 / 5 = 100,000
Again, we arrive at the answer: 100,000. This method is particularly useful when dealing with simpler percentages that can be easily expressed as fractions.
Method 3: Proportion Method
This method utilizes the concept of proportions to solve the problem. We set up a proportion where 'x' represents the unknown value (20% of 500,000):
20/100 = x/500,000
To solve for 'x', we cross-multiply:
100x = 20 * 500,000 100x = 10,000,000 x = 10,000,000 / 100 x = 100,000
This confirms our answer: 100,000. This method is helpful for understanding the proportional relationship between the percentage and the total value.
Beyond the Calculation: Real-World Applications
The ability to calculate percentages accurately is crucial across numerous disciplines. Let's explore some practical examples:
-
Finance: Calculating interest on loans, investments (compound interest calculations), discounts, taxes (VAT, sales tax), and profit margins all rely heavily on percentage calculations. Understanding 20% of 500,000 could represent the profit made on a large-scale investment or the tax levied on a significant transaction.
-
Statistics: Percentages are fundamental to expressing and interpreting statistical data. For example, if 500,000 people participated in a survey and 20% responded positively to a particular question, the result (100,000) provides a crucial insight into public opinion. This involves calculating percentages and understanding their representation within larger datasets.
-
Science: In scientific research, percentages often express the concentration of a substance in a solution, the success rate of an experiment, or the proportion of a population exhibiting a certain characteristic. Accuracy in percentage calculations is critical for the reliability of scientific findings.
-
Everyday Life: From calculating tips in restaurants to understanding sale discounts in stores, percentages are integral to our daily financial transactions. Knowing how to quickly calculate percentages can save you money and help you make informed decisions.
Common Misconceptions about Percentages
Several common misconceptions can lead to errors in percentage calculations. Let's clarify some of them:
-
Adding Percentages Directly: You cannot simply add percentages directly when dealing with different base values. For example, a 10% increase followed by a 10% decrease does not result in the original value. The base value changes after the first calculation.
-
Confusing Percentage Change with Absolute Change: A percentage change reflects the relative change, while the absolute change is the actual numerical difference. For instance, a 10% increase on 100 is 10, while a 10% increase on 1000 is 100. The percentage change is the same (10%), but the absolute change is vastly different.
-
Incorrect Interpretation of Percentage Points: Percentage points refer to the difference between two percentages, not the percentage of the difference. For example, an increase from 20% to 30% is a 10-percentage-point increase, not a 50% increase.
Frequently Asked Questions (FAQ)
-
How can I calculate a different percentage of 500,000? Simply replace "20" in the above calculations with the desired percentage and follow the same steps. For example, to find 15% of 500,000, you would calculate 0.15 * 500,000 = 75,000.
-
What are some online resources for practicing percentage calculations? Many websites and educational platforms offer interactive exercises and quizzes to help you improve your skills in percentage calculations.
-
Are there any shortcuts for calculating percentages mentally? While mental calculation for complex percentages is challenging, mastering simple fractions (like 1/2, 1/4, 1/5, 1/10) can assist in quick estimation.
Conclusion: Mastering Percentages for a Brighter Future
Understanding and mastering percentage calculations is a fundamental skill applicable across diverse areas of life. While finding 20% of 500,000 might seem trivial, the underlying principles and their applications are far-reaching and essential for navigating the complexities of finance, statistics, science, and everyday decision-making. By understanding the different methods of calculation, recognizing common misconceptions, and practicing regularly, you can confidently tackle percentage problems and unlock a deeper understanding of the world around you. The ability to perform accurate percentage calculations empowers you to make informed choices, analyze data critically, and succeed in various aspects of your personal and professional life. Remember, the key is not just to get the answer, but to understand the why behind the calculation.
Latest Posts
Latest Posts
-
In Which State In India
Sep 23, 2025
-
What Does A Chairperson Do
Sep 23, 2025
-
What Is An Llp Partnership
Sep 23, 2025
-
4 Letter Words Starting L
Sep 23, 2025
-
Shortcut For Highlighting In Word
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 20 Percent Of 500 000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.