2 X 1 X 4
candidatos
Sep 22, 2025 · 6 min read
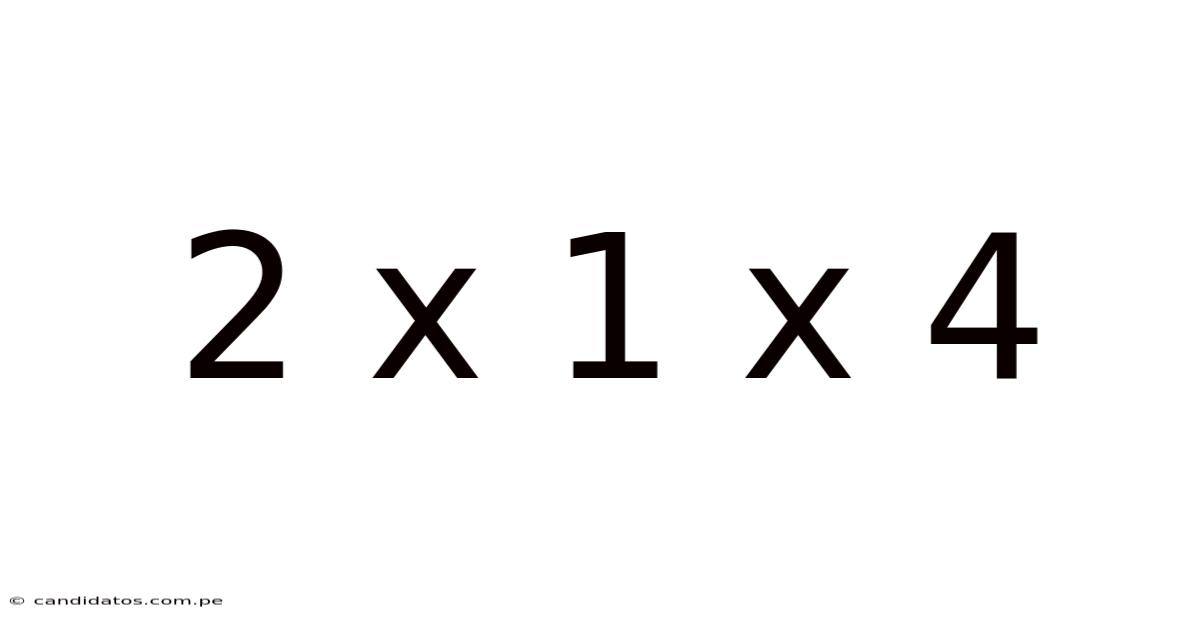
Table of Contents
Decoding 2 x 1 x 4: Exploring Dimensions, Volume, and Applications
This article delves into the seemingly simple expression "2 x 1 x 4," exploring its significance across various fields, from basic mathematics to advanced engineering and design. While appearing straightforward at first glance, understanding the implications of these three numbers unveils a surprisingly rich tapestry of concepts related to dimensions, volume calculations, and practical applications in construction, manufacturing, and even everyday life. We will dissect the meaning, explore its mathematical implications, delve into real-world applications, and answer frequently asked questions to provide a comprehensive understanding of this fundamental concept.
Understanding the Basics: Dimensions and Volume
The expression "2 x 1 x 4" fundamentally represents three dimensions: length, width, and height. These numbers usually denote measurements in a specific unit, such as inches, centimeters, or meters. In this case, we have:
- Length: 2 units
- Width: 1 unit
- Height: 4 units
These dimensions define a rectangular prism (or cuboid), a three-dimensional shape with six rectangular faces. Visualize a rectangular box: its length is 2 units, its width is 1 unit, and its height is 4 units. This simple representation has profound implications when we consider its volume.
The volume of a rectangular prism is calculated by multiplying its length, width, and height. Therefore, the volume of a shape with dimensions 2 x 1 x 4 is:
Volume = Length x Width x Height = 2 x 1 x 4 = 8 cubic units
This means that the rectangular prism can hold 8 cubes of the same unit size. Understanding this basic volume calculation is crucial in many areas, from packaging design to material estimations in construction projects.
Mathematical Implications: Beyond Simple Volume
While the volume calculation (8 cubic units) is straightforward, the expression "2 x 1 x 4" opens doors to more complex mathematical explorations. Let's consider a few:
-
Scale and Proportion: Changing one or more of the dimensions directly impacts the volume. Doubling the length (4 x 1 x 4) results in a volume of 16 cubic units, while doubling the height (2 x 1 x 8) also yields a volume of 16 cubic units. Understanding this relationship between dimensions and volume is essential for scaling designs and models.
-
Surface Area: The surface area of a rectangular prism is the sum of the areas of all its six faces. Calculating the surface area requires adding the areas of each face: two faces with area 2 x 1, two faces with area 2 x 4, and two faces with area 1 x 4. The total surface area for a 2 x 1 x 4 prism is 2(2 x 1) + 2(2 x 4) + 2(1 x 4) = 28 square units. This calculation is important in applications where surface treatment, coating, or material usage are relevant.
-
Variations and Transformations: The numbers 2, 1, and 4 can be rearranged, resulting in different shapes but the same volume. For example, a 1 x 2 x 4 prism, or a 4 x 2 x 1 prism, all have a volume of 8 cubic units. This illustrates the concept of volume conservation despite variations in shape.
Real-World Applications: From Construction to Packaging
The seemingly simple 2 x 1 x 4 dimensions are far from theoretical; they have practical applications across diverse fields:
1. Construction and Engineering:
-
Timber Framing: In carpentry and construction, lumber often comes in standard sizes. A 2 x 1 x 4 (in inches or centimeters depending on the measurement system) piece of wood is a common dimension used for various framing purposes, structural components, and support beams. Knowing the dimensions is vital for accurate material estimations and structural design.
-
Concrete Formwork: Formwork for pouring concrete often requires specific dimensions. Understanding the volume calculation allows for precise estimations of the amount of concrete needed.
-
Building Design: The understanding of these dimensional relationships helps architects and engineers in designing spaces with efficient use of volume and materials.
2. Manufacturing and Industry:
-
Packaging Design: Many products use packaging with dimensions based on these types of simple calculations. Optimizing package dimensions ensures efficient use of space, reducing material costs, and improving shipping logistics. A 2 x 1 x 4 box might represent an ideal size for a particular product range.
-
Shipping Containers: Similar to packaging, understanding dimensional relationships is crucial for optimizing the efficient use of space within shipping containers, minimizing transportation costs.
-
Machining and Tooling: In manufacturing processes, understanding dimensions is crucial for creating parts and components with precise measurements.
3. Everyday Applications:
-
Home Organization: Estimating the space required for storing items often involves visualizing rectangular prisms. A 2 x 1 x 4 foot shelf, for instance, has a specific storage capacity.
-
Gardening: Planning raised garden beds or understanding the volume of soil needed involves calculating dimensions of rectangular prisms.
-
DIY Projects: Numerous DIY projects rely on accurate dimensional measurements to build furniture, shelves, or other structures.
Frequently Asked Questions (FAQ)
Q: What units are typically used with 2 x 1 x 4 dimensions?
A: The units depend on the context. In construction, it might be inches (2 inches x 1 inch x 4 inches) or centimeters (2 cm x 1 cm x 4 cm). In larger-scale applications, it could be feet or meters. The unit must always be specified to avoid ambiguity.
Q: Are there other ways to represent the same volume of 8 cubic units?
A: Yes, many different sets of dimensions can result in the same volume. For example: 1 x 2 x 4, 1 x 1 x 8, 2 x 2 x 2, and so on. The number of possibilities is virtually infinite, allowing for design flexibility.
Q: How does the orientation of the dimensions (2 x 1 x 4 vs. 4 x 1 x 2) affect the application?
A: The orientation often significantly impacts practical application. In construction, a 2 x 1 x 4 timber might be used differently than a 4 x 1 x 2 timber due to strength considerations and how the wood grain is oriented. The orientation choice depends on the specific application's structural and functional requirements.
Q: What are some limitations of using simple dimensional analysis?
A: Simple dimensional analysis like 2 x 1 x 4 provides an idealized model. In reality, material imperfections, manufacturing tolerances, and other factors can affect the actual volume or dimensions of a physical object. More sophisticated analysis techniques may be needed for complex projects and precise engineering tasks.
Q: How can I improve my understanding of volume calculations?
A: Practice is key. Start with simple examples like 2 x 1 x 4 and work your way up to more complex shapes. Use visual aids like online calculators, 3D modelling software, or even physical blocks to grasp the concepts better. Solving various problems related to volume and surface area calculation helps develop a strong understanding.
Conclusion: The Profound Simplicity of 2 x 1 x 4
The seemingly simple expression "2 x 1 x 4" encapsulates a wealth of mathematical concepts and practical applications. Understanding its implications in terms of dimensions, volume, and surface area is crucial in various fields, ranging from construction and manufacturing to everyday life. While this article focused on rectangular prisms, the underlying principles extend to more complex shapes and situations. By mastering the basic principles illustrated here, individuals can develop a strong foundation for tackling more advanced mathematical and engineering challenges. The key takeaway is that even the simplest mathematical concepts can hold profound significance when applied to the real world. Continue exploring, practicing, and applying these fundamental ideas to unlock their full potential.
Latest Posts
Latest Posts
-
Square Cm To Square Meter
Sep 22, 2025
-
Fish That Start With T
Sep 22, 2025
-
5 Letter Words With Aj
Sep 22, 2025
-
Example Of Wheel And Axle
Sep 22, 2025
-
Periodic Table Of Elements H2o
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 2 X 1 X 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.