2 8 As A Percent
candidatos
Sep 22, 2025 · 5 min read
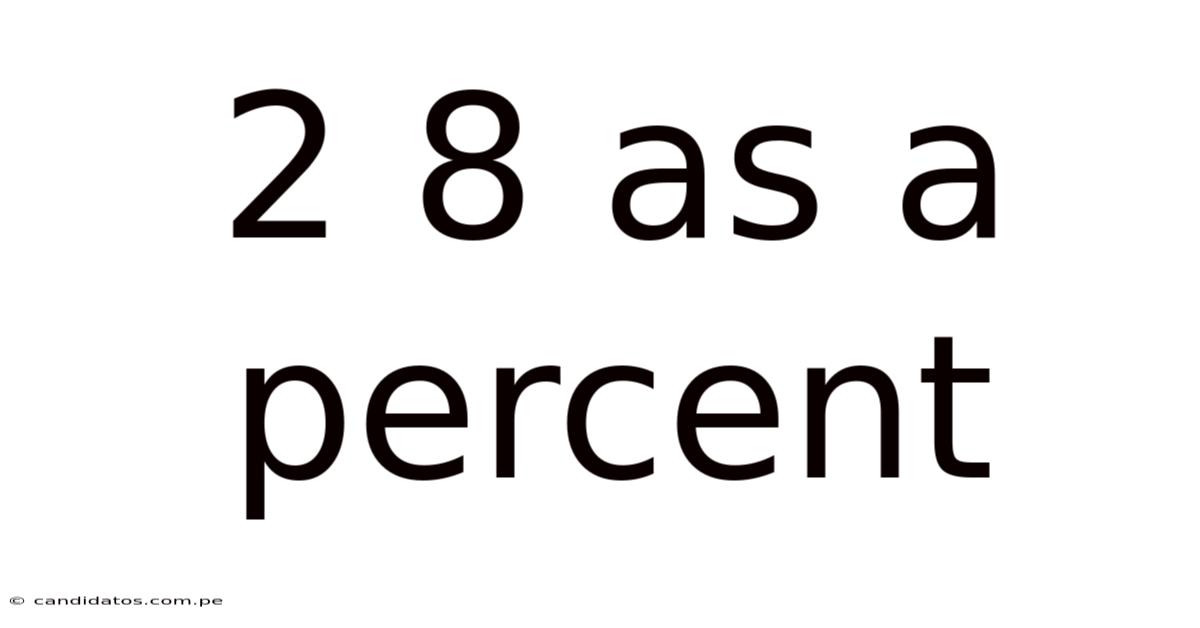
Table of Contents
Understanding 2/8 as a Percentage: A Comprehensive Guide
Understanding fractions and their percentage equivalents is a fundamental skill in mathematics with applications spanning various fields, from finance and cooking to science and engineering. This comprehensive guide will delve into the conversion of the fraction 2/8 into a percentage, exploring the underlying principles and providing practical examples to solidify your understanding. We'll also examine the broader concept of converting fractions to percentages, tackling common challenges and misconceptions along the way.
Introduction: Fractions, Decimals, and Percentages – A Triad of Representation
Numbers can be expressed in many forms. Fractions, decimals, and percentages are three common ways to represent parts of a whole. A fraction shows a part of a whole using a numerator (top number) and a denominator (bottom number). A decimal uses a base-ten system, representing parts of a whole using digits after a decimal point. A percentage expresses a fraction or decimal as parts per hundred, indicated by the symbol %. Understanding the relationships between these three representations is crucial for mathematical fluency. This article specifically focuses on converting the fraction 2/8 into its percentage equivalent.
Step-by-Step Conversion of 2/8 to a Percentage
There are two primary methods to convert the fraction 2/8 into a percentage:
Method 1: Simplifying the Fraction First
-
Simplify the Fraction: The fraction 2/8 can be simplified by finding the greatest common divisor (GCD) of the numerator and denominator. The GCD of 2 and 8 is 2. Dividing both the numerator and the denominator by 2, we get:
2/8 = 1/4
-
Convert the Simplified Fraction to a Decimal: To convert the fraction 1/4 to a decimal, divide the numerator (1) by the denominator (4):
1 ÷ 4 = 0.25
-
Convert the Decimal to a Percentage: To convert a decimal to a percentage, multiply the decimal by 100 and add the percentage symbol (%):
0.25 × 100 = 25%
Therefore, 2/8 is equal to 25%.
Method 2: Direct Conversion from Fraction to Percentage
-
Convert the Fraction to a Decimal: Divide the numerator (2) by the denominator (8):
2 ÷ 8 = 0.25
-
Convert the Decimal to a Percentage: Multiply the decimal by 100 and add the percentage symbol (%):
0.25 × 100 = 25%
This method yields the same result, demonstrating that simplifying the fraction beforehand is not strictly necessary but can simplify the calculation.
The Mathematical Explanation Behind the Conversion
The conversion from a fraction to a percentage fundamentally involves expressing the fraction as a proportion of 100. A percentage is simply a fraction with a denominator of 100. The process of converting a fraction to a percentage is essentially finding an equivalent fraction with a denominator of 100.
Let's break it down mathematically:
- We start with the fraction 2/8.
- We want to find the equivalent fraction x/100.
- To find x, we can set up a proportion: 2/8 = x/100
- Cross-multiplying, we get: 8x = 200
- Solving for x, we get: x = 200/8 = 25
- Therefore, 2/8 is equivalent to 25/100, which is 25%.
Practical Applications and Real-World Examples
Understanding how to convert fractions to percentages is vital in numerous real-world scenarios:
- Finance: Calculating interest rates, discounts, and profit margins often involves working with percentages. For example, if a store offers a 2/8 discount on an item, it means a 25% discount.
- Science: Percentages are widely used to express data and results in scientific studies and experiments. For instance, expressing the percentage of a certain element in a compound or the percentage of successful trials in an experiment.
- Cooking and Baking: Recipes often involve fractions, but understanding percentage equivalents allows for scaling recipes up or down easily.
- Data Analysis: Percentages are essential for interpreting statistical data, expressing proportions, and visualizing data in charts and graphs.
Frequently Asked Questions (FAQ)
-
Q: Can I convert any fraction to a percentage?
- A: Yes, any fraction can be converted to a percentage by following the steps outlined above.
-
Q: What if the decimal resulting from the fraction division is a long, repeating decimal?
- A: You can round the decimal to a certain number of decimal places before converting to a percentage. For instance, if the decimal is 0.3333..., you might round it to 0.33 and convert that to 33%. The level of precision required depends on the context.
-
Q: Is there a shortcut to convert fractions with a denominator of 100 directly to percentages?
- A: Yes! Fractions with a denominator of 100 convert directly to percentages. The numerator becomes the percentage value. For example, 30/100 = 30%.
-
Q: Why is understanding percentage important?
- A: Percentages provide a standardized way to compare and understand proportions. They make it easier to grasp relative amounts and are universally understood.
Conclusion: Mastering the Conversion from Fraction to Percentage
Converting fractions to percentages is a fundamental mathematical skill with far-reaching applications. By understanding the underlying principles and employing the methods outlined in this guide, you can confidently convert any fraction to its percentage equivalent. Remember the key steps: simplify the fraction (if possible), convert to a decimal by division, and then multiply by 100 to express the value as a percentage. Practice these steps regularly to build your fluency and confidence in working with fractions and percentages. Mastering this skill will empower you to tackle numerous problems across various disciplines and improve your overall mathematical proficiency. The ability to seamlessly navigate between fractions, decimals, and percentages is a crucial building block for more advanced mathematical concepts and real-world applications.
Latest Posts
Latest Posts
-
In Which State In India
Sep 23, 2025
-
What Does A Chairperson Do
Sep 23, 2025
-
What Is An Llp Partnership
Sep 23, 2025
-
4 Letter Words Starting L
Sep 23, 2025
-
Shortcut For Highlighting In Word
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 2 8 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.