2/3 Is Greater Than 1/2
candidatos
Sep 18, 2025 · 7 min read
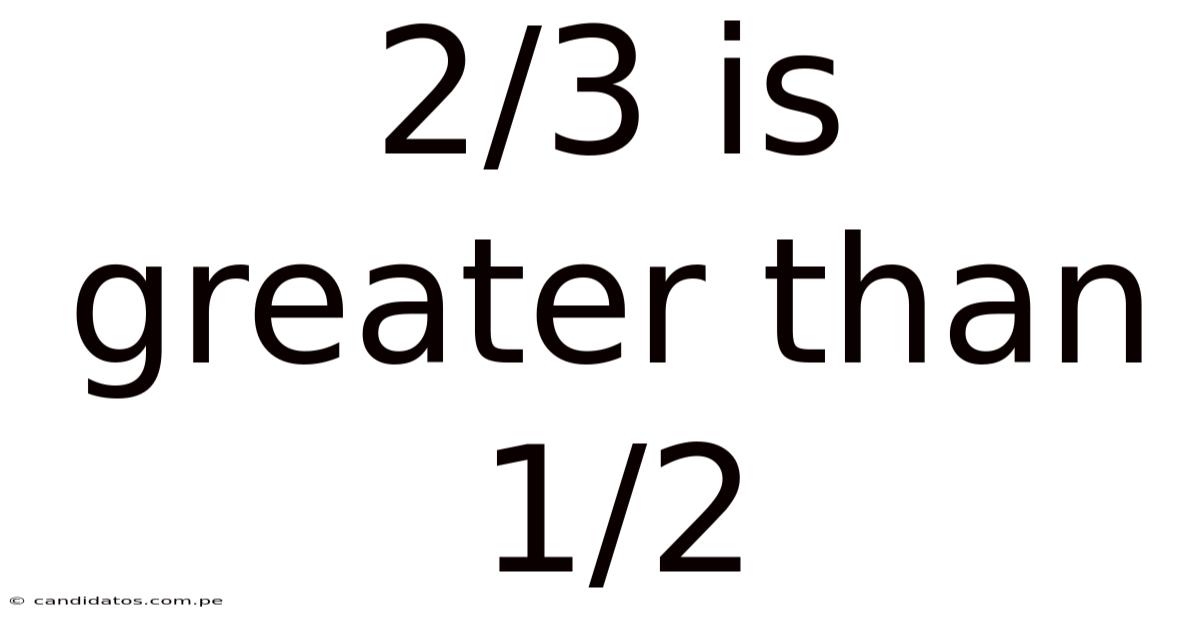
Table of Contents
2/3 is Greater Than 1/2: A Deep Dive into Fraction Comparison
Understanding fractions is a cornerstone of mathematical literacy. While seemingly simple, comparing fractions can be a source of confusion for many. This article will explore why 2/3 is greater than 1/2, not just through simple calculation but by delving into various methods of comparison, visualizing the fractions, and addressing common misconceptions. We'll also look at the broader implications of understanding fraction comparison in everyday life and further mathematical studies.
Introduction: Why Understanding Fraction Comparison Matters
The ability to compare fractions is crucial for a variety of reasons. From everyday tasks like dividing a pizza fairly to more advanced mathematical concepts like algebra and calculus, a solid grasp of fraction comparison is essential. Being able to quickly and confidently determine which fraction is larger is not just about getting the right answer; it's about developing a fundamental understanding of numerical relationships and proportional reasoning. This article aims to provide a comprehensive understanding of why 2/3 is greater than 1/2 and equip you with the tools to compare any two fractions.
Method 1: Finding a Common Denominator
One of the most common and reliable methods for comparing fractions is to find a common denominator. A common denominator is a number that is a multiple of both denominators. In this case, we're comparing 2/3 and 1/2. The denominators are 3 and 2. The least common multiple (LCM) of 3 and 2 is 6.
-
Converting the fractions:
- To convert 2/3 to a fraction with a denominator of 6, we multiply both the numerator and the denominator by 2: (2 x 2) / (3 x 2) = 4/6
- To convert 1/2 to a fraction with a denominator of 6, we multiply both the numerator and the denominator by 3: (1 x 3) / (2 x 3) = 3/6
-
Comparing the fractions: Now that both fractions have the same denominator, we can simply compare their numerators. Since 4 > 3, we can conclude that 4/6 > 3/6, therefore 2/3 > 1/2.
This method provides a clear and unambiguous way to compare fractions, making it a particularly useful approach for beginners. The principle of finding a common denominator works for comparing any two fractions, regardless of their complexity.
Method 2: Visual Representation using Fraction Bars
Visual aids can significantly enhance understanding, especially when dealing with abstract concepts like fractions. Imagine two identical bars representing a whole.
- Representing 1/2: Divide the first bar into two equal sections. Shade one section to represent 1/2.
- Representing 2/3: Divide the second bar into three equal sections. Shade two sections to represent 2/3.
By visually comparing the shaded portions of both bars, it becomes evident that the shaded area representing 2/3 is larger than the shaded area representing 1/2. This visual representation confirms that 2/3 > 1/2. This method is particularly helpful for those who learn best through visual means, providing a concrete illustration of the abstract concept. It’s a great method to use for teaching children about fractions.
Method 3: Converting to Decimals
Another way to compare fractions is to convert them into decimals. This method provides a numerical comparison that is often easier to understand intuitively.
- Converting 2/3 to a decimal: Divide the numerator (2) by the denominator (3): 2 ÷ 3 ≈ 0.666... (a repeating decimal)
- Converting 1/2 to a decimal: Divide the numerator (1) by the denominator (2): 1 ÷ 2 = 0.5
Comparing the decimal values, we see that 0.666... > 0.5, confirming that 2/3 > 1/2. While this method is straightforward, it's important to remember that some fractions, like 2/3, result in repeating decimals which might require rounding for practical comparisons. The accuracy depends on the level of precision required.
Method 4: Using Cross-Multiplication
Cross-multiplication offers a quick and efficient way to compare fractions, especially when dealing with larger numbers or fractions that are not easily converted to common denominators.
-
Cross-multiply: Multiply the numerator of the first fraction (2) by the denominator of the second fraction (2): 2 x 2 = 4
-
Cross-multiply: Multiply the numerator of the second fraction (1) by the denominator of the first fraction (3): 1 x 3 = 3
-
Compare the products: Since 4 > 3, we conclude that 2/3 > 1/2. This method works because it implicitly finds a common denominator (although it doesn't explicitly calculate it) and compares the resulting numerators.
While efficient, it’s important to remember that the larger product corresponds to the larger fraction only when comparing two fractions. This method is not directly applicable to comparing more than two fractions at a time.
Understanding the Numerator and Denominator
The numerator represents the number of parts you have, while the denominator represents the total number of equal parts the whole is divided into. In 2/3, you have 2 parts out of a total of 3 equal parts. In 1/2, you have 1 part out of a total of 2 equal parts. Understanding this fundamental concept is key to comparing fractions effectively.
Think of cutting a cake. If you have 2/3 of a cake, you have more cake than if you only have 1/2. This simple analogy illustrates the practical application of fraction comparison in real-world scenarios. The larger the numerator relative to the denominator, the larger the fraction.
Addressing Common Misconceptions
A common misconception is that the larger the denominator, the larger the fraction. This is incorrect. The denominator only indicates the size of each part, not the number of parts. For example, 1/10 is smaller than 1/2, even though 10 is larger than 2. The context of the numerator and denominator must be considered together.
Another misconception is assuming that adding the same number to both the numerator and the denominator will result in an equivalent fraction. This is generally false. Adding 1 to both the numerator and denominator of 1/2 (resulting in 2/3) changes the value of the fraction. These misconceptions highlight the importance of a thorough understanding of the underlying principles of fraction representation and comparison.
Fraction Comparison in Advanced Mathematics
The ability to compare fractions is fundamental to numerous advanced mathematical concepts. In algebra, understanding fraction comparison is critical for solving inequalities and manipulating equations involving fractions. In calculus, the concept extends to comparing areas under curves and evaluating limits involving fractions. Mastering fraction comparison lays a solid foundation for success in these advanced mathematical fields.
Real-World Applications Beyond Simple Calculations
The ability to compare fractions is not limited to mathematical exercises. It plays a vital role in various real-world situations:
- Cooking and Baking: Following recipes often involves working with fractions. Understanding fraction comparison ensures accurate measurements and successful outcomes.
- Finance: Calculating interest rates, proportions of investments, and understanding discounts all involve working with fractions.
- Construction and Engineering: Precise measurements are essential in construction and engineering, and a strong understanding of fractions helps ensure accuracy.
- Data Analysis: Representing and interpreting data often involves fractions and percentages, making fraction comparison a valuable skill.
Frequently Asked Questions (FAQ)
-
Q: Are there any other methods for comparing fractions besides the ones mentioned?
- A: Yes, there are other less common methods, such as converting fractions to percentages or using a number line. However, the methods described above are generally the most efficient and widely applicable.
-
Q: What if the fractions have very large denominators?
- A: For very large denominators, using a calculator to convert the fractions to decimals or employing cross-multiplication can be more efficient than finding a common denominator.
-
Q: Is there a quick way to determine if one fraction is larger than another without performing any calculations?
- A: While not always possible, if one fraction has a significantly larger numerator and a smaller denominator compared to another, it is likely larger. However, this is a heuristic and not a reliable method for all comparisons.
Conclusion: Mastering the Art of Fraction Comparison
Comparing fractions, while seemingly a simple task, is a fundamental skill that underpins a deeper understanding of mathematics and its real-world applications. This article has explored various methods for comparing fractions, emphasizing the importance of understanding the underlying principles of numerators and denominators. By mastering these methods and addressing common misconceptions, you will be well-equipped to confidently compare any two fractions and apply this knowledge in diverse contexts. Remember, the ability to compare fractions is not just about finding the right answer; it's about developing a solid understanding of numerical relationships and proportional reasoning, which is a valuable skill throughout life. Through practice and understanding, comparing fractions can become second nature, unlocking a deeper appreciation for the beauty and power of mathematics.
Latest Posts
Latest Posts
-
Year 8 Cambridge Maths Textbook
Sep 18, 2025
-
Form Of Triangle Crossword Clue
Sep 18, 2025
-
Eukaryote And Prokaryote Venn Diagram
Sep 18, 2025
-
Words With The Re Prefix
Sep 18, 2025
-
33 40 As A Percent
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 2/3 Is Greater Than 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.