19 25 As A Percentage
candidatos
Sep 19, 2025 · 5 min read
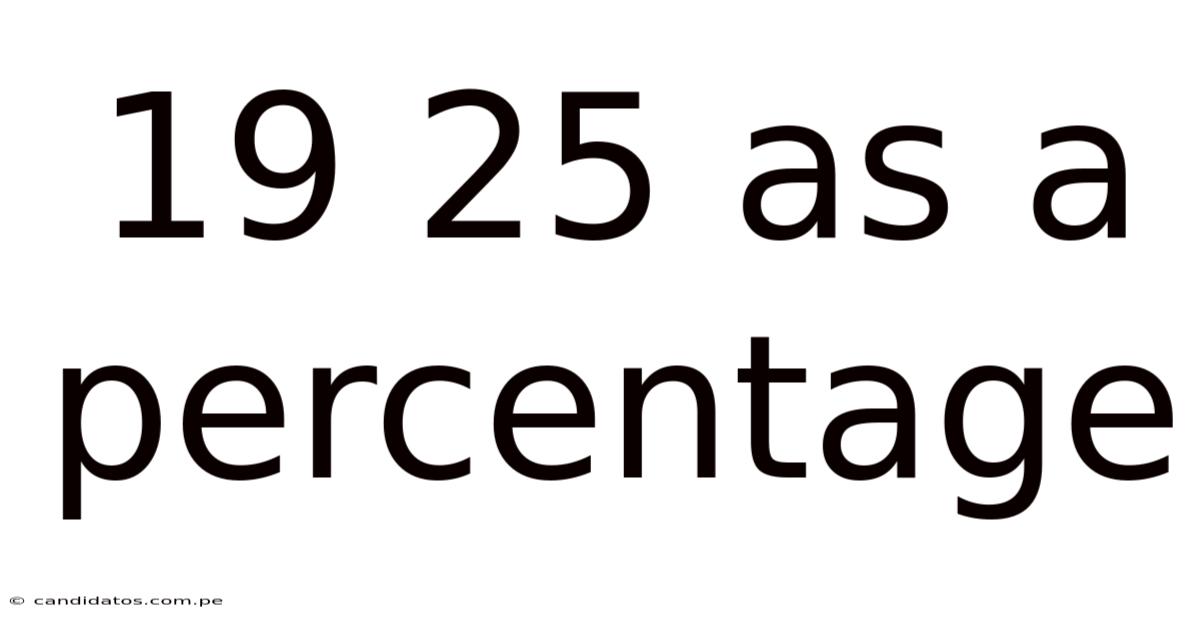
Table of Contents
19/25 as a Percentage: A Comprehensive Guide to Fraction-to-Percentage Conversion
Understanding how to convert fractions to percentages is a fundamental skill in mathematics, crucial for various applications from everyday budgeting to advanced statistical analysis. This article will provide a detailed explanation of how to calculate 19/25 as a percentage, offering multiple approaches and exploring the underlying concepts. We'll delve into the process, provide examples, address common questions, and explore related percentage calculations. By the end, you'll not only know the answer but also grasp the broader principles of fraction-to-percentage conversion.
Understanding Fractions and Percentages
Before diving into the calculation, let's refresh our understanding of fractions and percentages. A fraction represents a part of a whole, expressed as a ratio of two numbers – the numerator (top number) and the denominator (bottom number). For instance, in the fraction 19/25, 19 represents the part and 25 represents the whole.
A percentage, denoted by the symbol %, represents a fraction of 100. It expresses a proportion out of 100, providing a standardized way to compare different fractions or proportions. For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100, or simplified, 1/2.
Method 1: Direct Conversion using Division
The most straightforward method to convert a fraction to a percentage is through division. Here's how to calculate 19/25 as a percentage:
-
Divide the numerator by the denominator: Divide 19 by 25. This gives you 0.76.
-
Multiply by 100: Multiply the result (0.76) by 100 to express it as a percentage. This yields 76.
Therefore, 19/25 is equal to 76%.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
Another approach involves finding an equivalent fraction with a denominator of 100. This method is particularly useful when dealing with fractions that can be easily scaled to a denominator of 100.
-
Determine the scaling factor: To convert the denominator of 25 to 100, we need to multiply it by 4 (25 x 4 = 100).
-
Apply the scaling factor to the numerator: We must also multiply the numerator by the same factor (19 x 4 = 76).
-
Express as a percentage: The equivalent fraction becomes 76/100, which directly translates to 76%.
This method highlights the relationship between fractions and percentages, clearly showing that 76 out of 100 is equivalent to 76%.
Method 3: Using Proportions
The concept of proportions offers another insightful way to approach this conversion. A proportion is a statement that two ratios are equal. We can set up a proportion to solve for the percentage:
19/25 = x/100
To solve for x (the percentage), we cross-multiply:
19 * 100 = 25 * x
1900 = 25x
x = 1900 / 25
x = 76
Therefore, x = 76%. This method reinforces the idea of equivalent ratios and provides a systematic approach to solving for the unknown percentage.
Practical Applications and Real-World Examples
Understanding percentage calculations is invaluable in many aspects of daily life:
-
Academic Performance: If a student answers 19 out of 25 questions correctly on a test, their score is 76%.
-
Sales and Discounts: A store offering a 76% discount on an item means the customer pays only 24% of the original price.
-
Financial Calculations: Calculating interest rates, profit margins, and tax percentages all rely on the ability to convert fractions to percentages.
-
Data Analysis: Interpreting statistical data often involves converting fractions or ratios into percentages for easier understanding and comparison.
Further Exploration: Calculating Related Percentages
Let's extend our understanding by exploring calculations related to 19/25:
-
Calculating the remaining percentage: If 19/25 represents a certain portion, the remaining portion is 6/25 (25 - 19 = 6). Converting 6/25 to a percentage using any of the methods above gives us 24%. This demonstrates that the sum of the two percentages (76% + 24%) equals 100%, representing the whole.
-
Scaling the fraction: What if we had 38/50? This fraction is equivalent to 19/25 (both numerator and denominator are multiplied by 2), so it also equals 76%. This illustrates the concept of equivalent fractions and how they represent the same proportion.
-
Working with larger numbers: Imagine a scenario where you have 190 items out of 250. This is still equivalent to 19/25, resulting in the same 76% because the ratio remains constant.
Frequently Asked Questions (FAQ)
-
Q: Why is multiplying by 100 necessary when converting a decimal to a percentage?
A: A percentage is defined as a fraction of 100. Multiplying by 100 scales the decimal value to represent it as a proportion out of 100, effectively converting it into a percentage.
-
Q: Can I use a calculator to convert fractions to percentages?
A: Yes, most calculators have a division function that allows you to directly compute the decimal equivalent of a fraction, which can then be multiplied by 100 to obtain the percentage.
-
Q: What if the fraction results in a repeating decimal?
A: In such cases, you can round the decimal to a reasonable number of decimal places before multiplying by 100 to get an approximate percentage. For example, if the fraction yielded 0.3333..., you might round it to 0.33 and then multiply by 100 to get 33%. The level of precision needed depends on the context of the problem.
-
Q: Are there any other methods for converting fractions to percentages?
A: While the methods described are the most common and efficient, there are other approaches involving using proportions with different reference values besides 100. However, these methods often involve more complex calculations without significant added benefits.
Conclusion
Converting fractions to percentages is a fundamental mathematical skill with far-reaching applications. This article has demonstrated three different methods for converting 19/25 to a percentage, clarifying the underlying principles and providing real-world examples. By understanding these methods and the concepts of fractions, percentages, and proportions, you'll be well-equipped to tackle a wide variety of percentage calculations with confidence. Remember that the key is to understand the relationship between fractions and percentages, and to choose the method most suitable for the specific problem at hand. Practice is essential for mastering these concepts; the more you work with these calculations, the more intuitive they will become.
Latest Posts
Latest Posts
-
Advantages And Disadvantages Sole Trader
Sep 19, 2025
-
How To Calculate Electricity Usage
Sep 19, 2025
-
4 Letter Word With Aq
Sep 19, 2025
-
Who Discovered The Element Carbon
Sep 19, 2025
-
Dividing Decimals With Decimals Worksheet
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 19 25 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.