13 65 As A Percentage
candidatos
Sep 23, 2025 · 5 min read
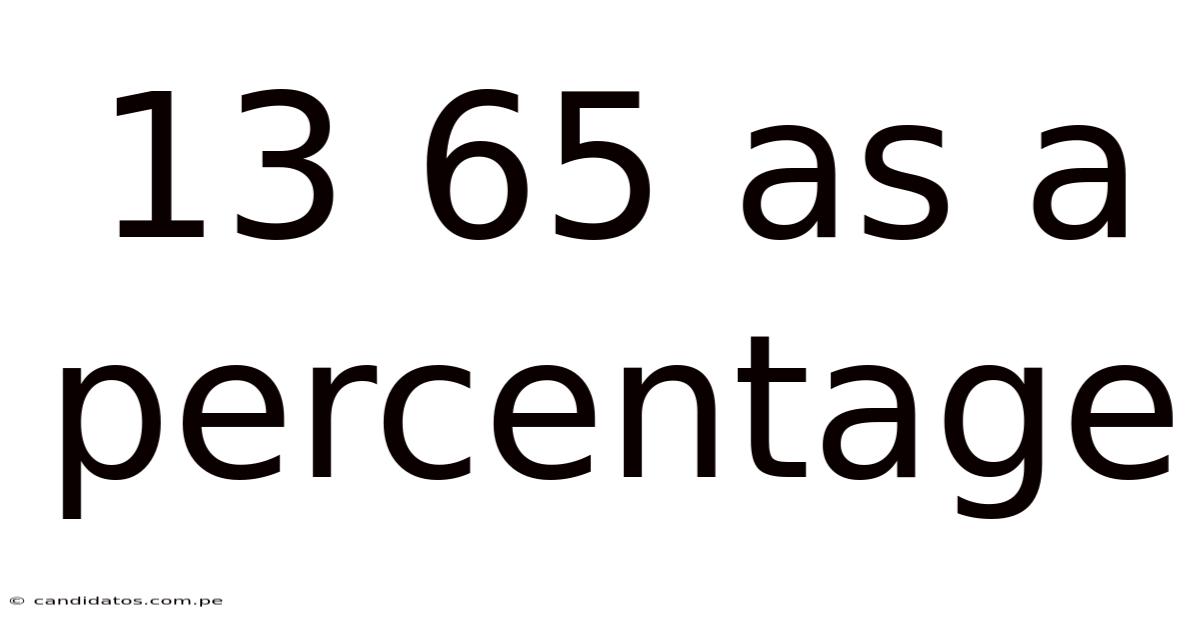
Table of Contents
Understanding 13/65 as a Percentage: A Comprehensive Guide
Calculating percentages is a fundamental skill in mathematics with widespread applications in everyday life, from calculating discounts and taxes to understanding statistical data and financial reports. This article will delve into the detailed process of converting the fraction 13/65 into a percentage, exploring various methods and providing a deeper understanding of the underlying concepts. We'll cover different approaches, including the direct calculation method, the decimal method, and practical applications, ensuring a thorough grasp of this important mathematical concept. This comprehensive guide aims to clarify how to determine what 13 out of 65 represents as a percentage and why this conversion is valuable.
Introduction: Fractions, Decimals, and Percentages
Before jumping into the calculation of 13/65 as a percentage, let's briefly review the relationships between fractions, decimals, and percentages. These three represent different ways of expressing parts of a whole.
-
Fraction: A fraction represents a part of a whole, expressed as a ratio of two numbers – the numerator (top number) and the denominator (bottom number). For example, 13/65 means 13 parts out of a total of 65 parts.
-
Decimal: A decimal represents a part of a whole using the base-10 system. It's expressed using a decimal point to separate the whole number part from the fractional part.
-
Percentage: A percentage represents a part of a whole as a fraction of 100. It's denoted by the symbol "%" and indicates "out of 100". For instance, 20% means 20 out of 100.
Method 1: Direct Calculation
The most straightforward method to convert a fraction to a percentage involves two simple steps:
-
Divide the numerator by the denominator: This gives you the decimal equivalent of the fraction. In our case, 13 divided by 65 is:
13 ÷ 65 = 0.2
-
Multiply the decimal by 100: This converts the decimal to a percentage. Multiplying 0.2 by 100 gives:
0.2 x 100 = 20
Therefore, 13/65 is equal to 20%.
Method 2: Simplifying the Fraction First
Often, simplifying the fraction before converting to a percentage can make the calculation easier. This involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it.
The GCD of 13 and 65 is 13. Dividing both the numerator and denominator by 13, we get:
13 ÷ 13 = 1 65 ÷ 13 = 5
This simplifies the fraction to 1/5. Now, we can convert this simplified fraction to a percentage:
1 ÷ 5 = 0.2 0.2 x 100 = 20%
As expected, we arrive at the same answer: 20%. Simplifying the fraction beforehand can be particularly helpful when dealing with larger numbers.
Method 3: Using Proportions
Another approach involves setting up a proportion. We know that a percentage is a fraction out of 100. So, we can set up the following proportion:
13/65 = x/100
To solve for x (the percentage), we can cross-multiply:
65x = 1300
Now, divide both sides by 65:
x = 1300 ÷ 65 = 20
Therefore, x = 20, meaning 13/65 is 20%.
Understanding the Result: What Does 20% Mean?
The result, 20%, signifies that 13 represents 20% of 65. This means that if you divide 65 into 100 equal parts, 13 would occupy 20 of those parts. This percentage representation provides a concise and easily understandable way to express the relationship between 13 and 65.
Practical Applications of Percentage Calculations
Calculating percentages has numerous practical applications in various fields:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns.
-
Retail: Determining sale prices, calculating markups, and analyzing sales data.
-
Statistics: Representing data in a clear and concise manner, making comparisons easier to understand.
-
Science: Expressing experimental results, calculating error margins, and representing data in graphs and charts.
-
Everyday Life: Calculating tips, splitting bills, understanding nutritional information, and much more.
Expanding on the Concept: Working with Percentages in Reverse
Understanding how to calculate a percentage is crucial, but it's equally important to understand how to work with percentages in reverse. For example:
-
Finding a percentage of a number: What is 20% of 65? This is calculated as (20/100) * 65 = 13. This confirms our original fraction.
-
Finding the original number from a percentage: If 20% of a number is 13, what is the original number? This can be solved using the formula: Original Number = (Percentage Number / Percentage) * 100. In this case, (13 / 20) * 100 = 65.
These reverse calculations are equally important in practical applications.
Frequently Asked Questions (FAQ)
Q1: Can I use a calculator to convert 13/65 to a percentage?
A1: Yes, absolutely! Most calculators have a percentage function. Simply divide 13 by 65 and then multiply the result by 100.
Q2: What if the fraction doesn't simplify easily?
A2: Even if the fraction doesn't simplify easily, the direct calculation method (dividing the numerator by the denominator and multiplying by 100) will always work.
Q3: Are there any online tools that can help with percentage calculations?
A3: Yes, many online calculators and converters are readily available to assist with percentage calculations.
Q4: Why is understanding percentages important?
A4: Percentages provide a standardized way to compare proportions and make sense of numerical data in various contexts. They are essential for understanding financial information, statistical data, and numerous everyday situations.
Q5: What if I have a more complex fraction?
A5: The same principles apply. Divide the numerator by the denominator and multiply the result by 100 to convert any fraction to a percentage. Simplifying the fraction first can often make the calculation easier.
Conclusion: Mastering Percentage Calculations
Converting fractions to percentages is a fundamental skill that finds application in diverse fields. This article has explored various methods for converting 13/65 to a percentage, demonstrating that the answer is 20%. We've also examined the practical implications of percentage calculations and addressed frequently asked questions. Mastering these techniques will enhance your mathematical skills and provide valuable tools for tackling various problems in your academic and professional life. Remember that understanding the underlying concepts, not just the formula, is key to truly grasping the power of percentage calculations. Practice with different fractions and you'll soon become proficient in converting fractions to percentages and using this knowledge effectively in various contexts.
Latest Posts
Latest Posts
-
Converting Fractions Into Decimals Worksheet
Sep 23, 2025
-
Words That Start With Sch
Sep 23, 2025
-
What Is 5 Of 200000
Sep 23, 2025
-
Words That Start With Ao
Sep 23, 2025
-
Words To Describe My Father
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 13 65 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.