12 8 Divided By 4
candidatos
Sep 21, 2025 · 6 min read
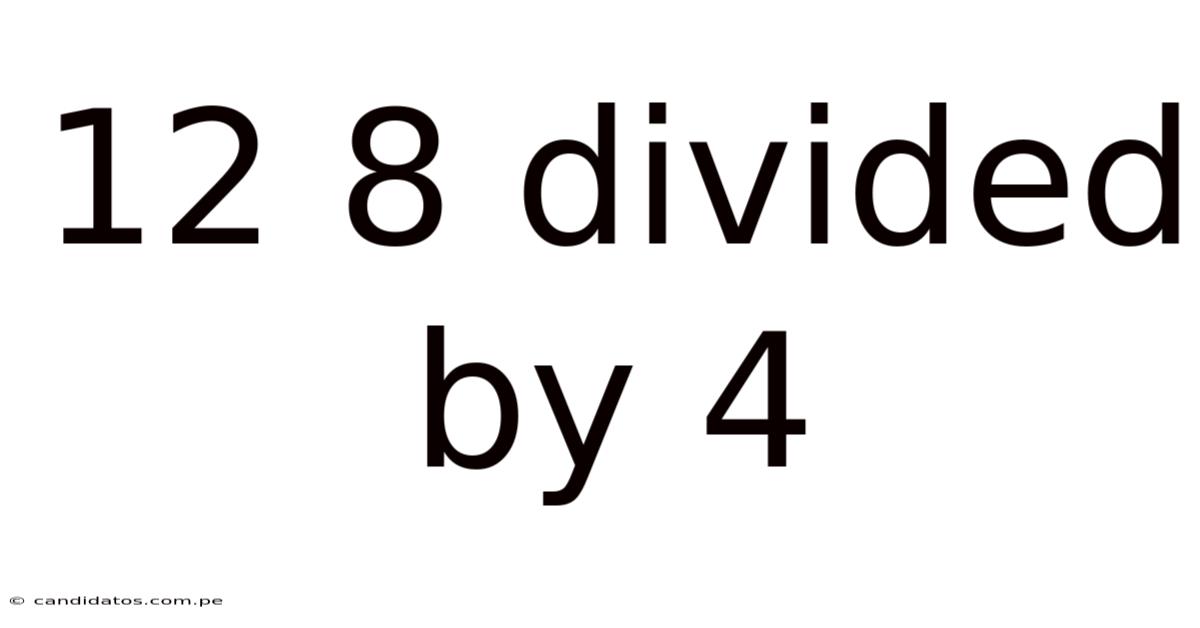
Table of Contents
Decoding 12/8 Divided by 4: A Deep Dive into Fraction Division
This article explores the seemingly simple mathematical problem of 12/8 divided by 4, providing a comprehensive understanding of the process, its underlying principles, and practical applications. We'll unpack the steps involved, explain the reasoning behind each stage, and address common misconceptions. Understanding this seemingly basic calculation forms a crucial foundation for more complex mathematical concepts later on. Whether you're a student struggling with fractions or an adult looking to refresh your math skills, this guide will empower you with a clear and confident approach to solving fraction division problems.
Understanding Fractions: A Quick Refresher
Before diving into the division, let's briefly revisit the concept of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates the number of parts we have, while the denominator shows the total number of equal parts the whole is divided into. For instance, in the fraction 12/8, 12 represents the number of parts, and 8 represents the total number of equal parts.
This particular fraction, 12/8, is also known as an improper fraction because the numerator (12) is larger than the denominator (8). Improper fractions can be converted into mixed numbers, which consist of a whole number and a proper fraction (where the numerator is smaller than the denominator). In this case, 12/8 simplifies to 3/2 or 1 ½. Understanding this conversion is vital for solving our division problem efficiently.
Step-by-Step Solution: 12/8 ÷ 4
Now let's tackle the core problem: 12/8 divided by 4. We can approach this in several ways, each offering valuable insights into the principles of fraction division.
Method 1: Converting to a Mixed Number and then Dividing
-
Convert the improper fraction to a mixed number: As mentioned earlier, 12/8 simplifies to 1 ½ or 3/2.
-
Divide the mixed number by 4: Dividing a mixed number by a whole number can be slightly tricky. One approach is to convert the mixed number back into an improper fraction: 1 ½ = 3/2. Now we have 3/2 ÷ 4.
-
Convert the whole number into a fraction: To divide fractions, it's helpful to express the whole number (4) as a fraction: 4/1. This allows us to apply the rules of fraction division consistently. Now our problem is 3/2 ÷ 4/1.
-
Invert the second fraction and multiply: The key rule for dividing fractions is to invert (flip) the second fraction and then multiply. Inverting 4/1 gives us 1/4. So, we now have (3/2) x (1/4).
-
Multiply the numerators and the denominators: Multiply the numerators (top numbers) together: 3 x 1 = 3. Multiply the denominators (bottom numbers) together: 2 x 4 = 8. This gives us the final answer: 3/8.
Method 2: Directly Dividing the Improper Fraction
Alternatively, we can work directly with the improper fraction 12/8:
-
Rewrite the division as a multiplication: Similar to Method 1, we rewrite the division as a multiplication by inverting the second fraction (4/1 becomes 1/4). Our problem now is (12/8) x (1/4).
-
Multiply the numerators and denominators: Multiply the numerators: 12 x 1 = 12. Multiply the denominators: 8 x 4 = 32. This gives us 12/32.
-
Simplify the fraction: Notice that both 12 and 32 are divisible by 4. Simplifying the fraction by dividing both the numerator and denominator by 4, we get 3/8.
Both methods yield the same result: 3/8. Choosing the method that feels most comfortable and intuitive is key. The important takeaway is the consistent application of fraction division rules.
The Underlying Mathematical Principles
The process of dividing fractions hinges on the fundamental concept of reciprocals. The reciprocal of a fraction is simply the fraction inverted. When we divide by a fraction, we are essentially multiplying by its reciprocal. This is because division is the inverse operation of multiplication.
Consider the problem a/b ÷ c/d. This can be rewritten as (a/b) x (d/c). This manipulation is based on the properties of multiplicative inverses. Each fraction has a reciprocal which, when multiplied, results in 1 (e.g., (2/3) x (3/2) = 1). Using this property allows us to transform division into a more manageable multiplication.
Practical Applications: Real-World Examples
Understanding fraction division isn't just about solving textbook problems; it has significant practical applications in various real-world scenarios:
-
Cooking and Baking: Recipes often require fractional measurements. If a recipe calls for 12/8 cups of flour and you want to make only 1/4 of the recipe, you'll need to divide the flour amount by 4.
-
Construction and Measurement: Many construction projects involve precise measurements using fractions of inches or feet. Dividing fractional measurements is essential for accurate calculations and efficient work.
-
Data Analysis and Statistics: In statistics, calculating averages or proportions often involves dividing fractional values.
-
Sewing and Fabric Cutting: Tailors and seamstresses frequently work with fractional measurements of fabric. Dividing fractional amounts accurately is crucial for ensuring precise cutting and fitting.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to solve this problem?
A: Yes, most calculators can handle fraction division. However, understanding the underlying principles is crucial for developing a strong mathematical foundation and for solving more complex problems where a calculator might not be readily available.
Q: What if the fraction was a different improper fraction?
A: The process remains the same. You would still convert the improper fraction to a mixed number or proceed directly with the fraction division rules (inverting the second fraction and multiplying).
Q: Why is it important to simplify the fraction at the end?
A: Simplifying a fraction to its lowest terms presents the answer in its most concise and understandable form. It also makes further calculations or comparisons easier.
Q: What if I'm dividing by a decimal instead of a whole number?
A: You would first convert the decimal to a fraction, and then apply the same rules for fraction division.
Conclusion: Mastering Fraction Division
Dividing fractions, even seemingly simple ones like 12/8 ÷ 4, requires a thorough understanding of fundamental mathematical principles. By systematically following the steps outlined in this article, and by grasping the concept of reciprocals, you can confidently tackle similar problems and apply this knowledge to various real-world applications. Remember, practice is key. The more you work with fractions, the more intuitive and comfortable you'll become with solving these types of problems. This fundamental skill builds a solid base for tackling more advanced mathematical concepts in the future. Don't hesitate to revisit this guide and practice different variations of fraction division problems to solidify your understanding. With consistent effort and practice, mastering fraction division will be a rewarding achievement.
Latest Posts
Latest Posts
-
Words Containing Z And Y
Sep 21, 2025
-
Words With Z Three Letters
Sep 21, 2025
-
Five Letter Words With Av
Sep 21, 2025
-
Definition Of Summation Of Forces
Sep 21, 2025
-
Things That Rhyme With Us
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 12 8 Divided By 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.