10 8 As A Decimal
candidatos
Sep 21, 2025 · 5 min read
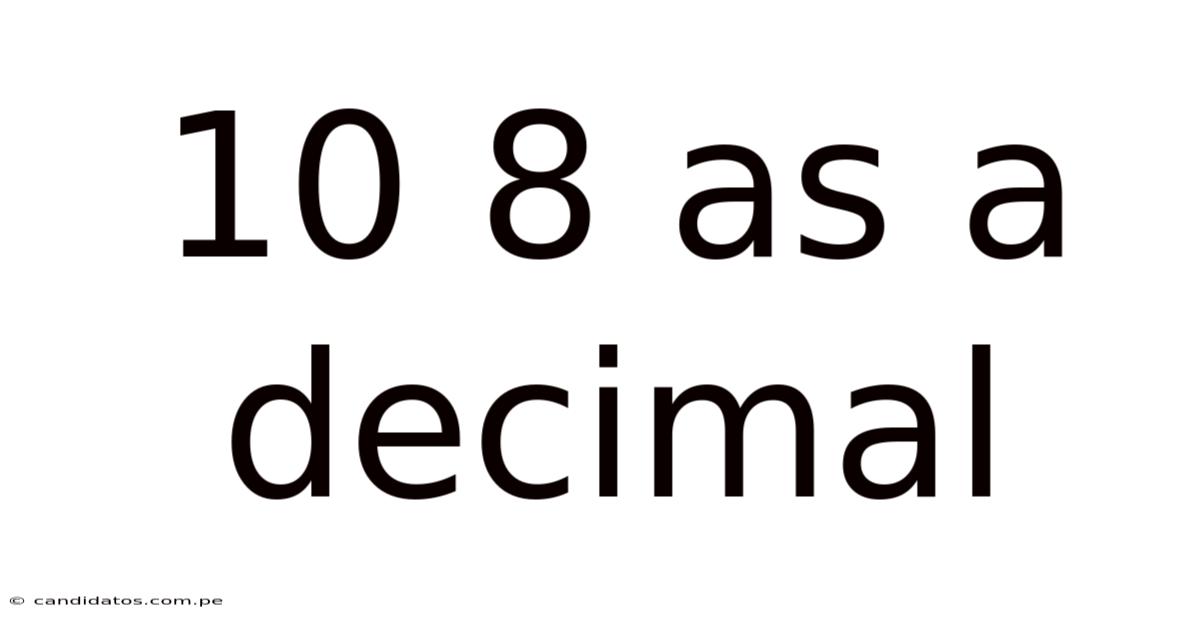
Table of Contents
Decoding 10/8 as a Decimal: A Comprehensive Guide
Understanding fractions and their decimal equivalents is fundamental to mathematics and numerous real-world applications. This article delves into the conversion of the fraction 10/8 into its decimal form, exploring the process step-by-step and providing a deeper understanding of the underlying principles. We'll cover various methods, address common misconceptions, and even explore the practical applications of this seemingly simple conversion.
Introduction: Understanding Fractions and Decimals
Before we dive into the specifics of converting 10/8, let's briefly refresh our understanding of fractions and decimals. A fraction represents a part of a whole, consisting of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, and the denominator indicates how many equal parts the whole is divided into.
A decimal, on the other hand, is a way of expressing a number using base-10, where each digit represents a power of 10. The decimal point separates the whole number part from the fractional part. For example, 12.34 represents 1 ten, 2 ones, 3 tenths, and 4 hundredths.
Converting a fraction to a decimal involves finding the equivalent decimal representation of the fraction. This is often done through division.
Method 1: Direct Division
The most straightforward method to convert 10/8 to a decimal is through direct division. We divide the numerator (10) by the denominator (8):
10 ÷ 8 = 1.25
Therefore, 10/8 as a decimal is 1.25. This method is simple and effective for most fractions.
Method 2: Simplifying the Fraction First
Before performing the division, we can simplify the fraction 10/8. Both the numerator and denominator are divisible by 2:
10 ÷ 2 = 5 8 ÷ 2 = 4
This simplifies the fraction to 5/4. Now, we perform the division:
5 ÷ 4 = 1.25
As you can see, simplifying the fraction first doesn't change the final decimal result; it just makes the division slightly easier. This is a helpful strategy, especially when dealing with larger fractions.
Method 3: Understanding the Remainder and Long Division
Let's delve a little deeper into the division process, using long division. This will help illustrate the concept more clearly:
1.25
8 | 10.00
8
--
20
16
--
40
40
--
0
We start by dividing 8 into 10. 8 goes into 10 once (1), leaving a remainder of 2. We add a zero and bring it down, making it 20. 8 goes into 20 twice (2), leaving a remainder of 4. We add another zero and bring it down, making it 40. 8 goes into 40 five times (5), leaving a remainder of 0. The final answer is 1.25. This demonstrates that the remainder is crucial in determining the decimal value.
Exploring the Concept of Improper Fractions
The fraction 10/8 is an example of an improper fraction, where the numerator is larger than or equal to the denominator. Improper fractions always result in a decimal greater than or equal to 1. This is in contrast to a proper fraction, where the numerator is smaller than the denominator, resulting in a decimal less than 1. Converting improper fractions to decimals often results in a mixed number or a decimal larger than 1.
Converting to a Mixed Number
Another way to represent 10/8 is as a mixed number. A mixed number combines a whole number and a proper fraction. To convert 10/8 to a mixed number, we perform the division:
10 ÷ 8 = 1 with a remainder of 2
This means 10/8 is equal to 1 and 2/8. We can further simplify 2/8 to 1/4. Therefore, 10/8 can be expressed as the mixed number 1 1/4.
Decimal Representation and Real-World Applications
The decimal equivalent of 10/8, 1.25, has many practical applications. For example:
- Measurement: If you're measuring something and your ruler only shows increments of 1/8 of an inch, 10/8 of an inch would be 1.25 inches.
- Finance: If you divide $10 among 8 people equally, each person receives $1.25.
- Baking: If a recipe calls for 10/8 cups of flour, you would measure 1 and 1/4 cups of flour.
- Data Analysis: In statistical calculations or data analysis, working with decimal representations is often more convenient than fractions.
Addressing Common Misconceptions
A common mistake when converting fractions to decimals is forgetting to continue the division until there's no remainder or the decimal repeats. Always ensure you've carried out the division completely. Another frequent error arises from incorrectly simplifying the fraction before the division. Make sure to simplify correctly; otherwise, you may end up with an incorrect decimal value.
Frequently Asked Questions (FAQ)
-
Q: Can all fractions be converted to terminating decimals? A: No. Fractions with denominators that have prime factors other than 2 and 5 (e.g., 3, 7, 11) will result in repeating or non-terminating decimals.
-
Q: What if I get a repeating decimal? A: Repeating decimals are represented by placing a bar over the repeating digits. For example, 1/3 is represented as 0.3̅.
-
Q: Is it always necessary to simplify the fraction before converting it to a decimal? A: No, it's not strictly necessary, but simplifying can make the division easier and less prone to errors.
-
Q: How do I convert a decimal back into a fraction? A: For terminating decimals, you can write the decimal as a fraction with a denominator that's a power of 10 (10, 100, 1000, etc.), and then simplify the fraction. For example, 0.25 can be written as 25/100, which simplifies to 1/4.
Conclusion: Mastering Fraction-to-Decimal Conversions
Converting fractions like 10/8 to their decimal equivalents is a fundamental skill in mathematics. Understanding the different methods, including direct division, simplifying the fraction first, and using long division, provides a solid foundation for tackling more complex fraction-to-decimal conversions. Remember, the key is to perform the division accurately and understand the concept of remainders, whether the fraction is proper or improper. This knowledge is not just about solving mathematical problems; it's about gaining a deeper appreciation for the interconnectedness of numerical representations and their practical applications in everyday life. Through consistent practice and a firm grasp of the underlying principles, you can confidently navigate the world of fractions and decimals.
Latest Posts
Latest Posts
-
Words That Rhyme With Change
Sep 21, 2025
-
Hindi No 1 To 100
Sep 21, 2025
-
Descriptive Words For Best Friend
Sep 21, 2025
-
Positive Adjectives Beginning With R
Sep 21, 2025
-
Grey Bird With Black Face
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 10 8 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.