1 Divided By 3 4
candidatos
Sep 21, 2025 · 5 min read
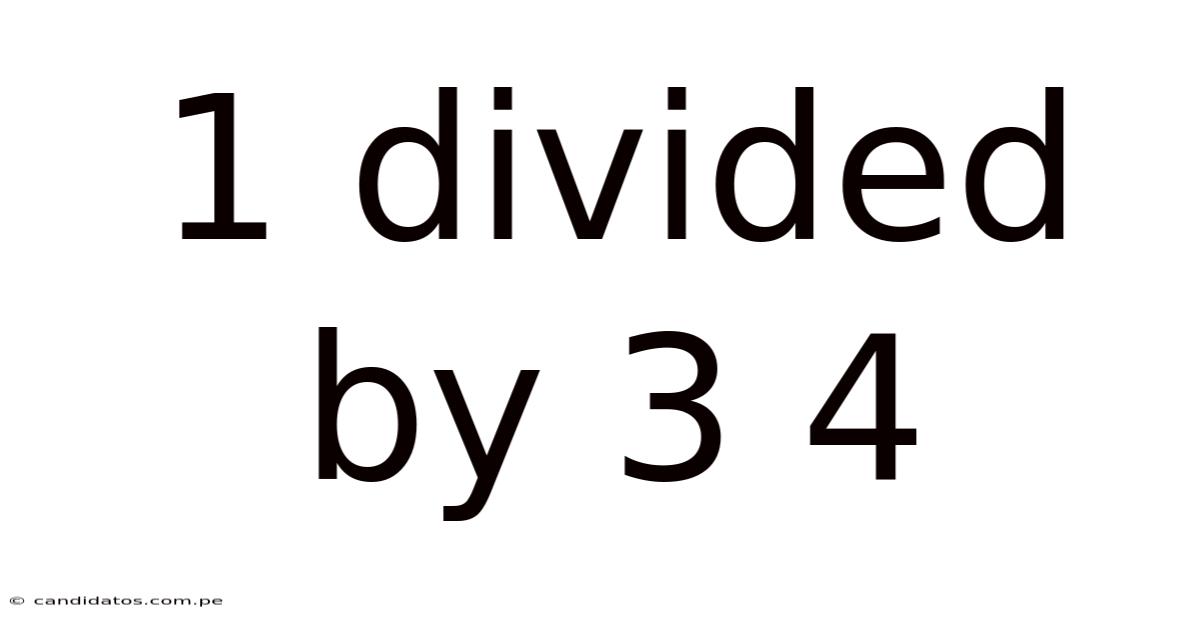
Table of Contents
Decoding 1 Divided by 3/4: A Deep Dive into Fractions and Division
Understanding how to divide by fractions is a fundamental concept in mathematics, often causing confusion for students. This comprehensive guide will break down the process of calculating 1 divided by 3/4, explaining not only the mechanics but also the underlying mathematical principles. We'll explore different approaches, answer frequently asked questions, and provide a firm foundation for tackling more complex fraction problems. This article covers various methods, ensuring you grasp the concept fully, no matter your mathematical background.
Introduction: Understanding the Problem
The question, "What is 1 divided by 3/4?", might seem straightforward at first glance. However, dividing by a fraction requires a deeper understanding of fractional arithmetic. The key lies in recognizing that dividing by a fraction is the same as multiplying by its reciprocal. This seemingly simple shift in perspective opens the door to a clear and efficient solution. We'll explore this concept in detail throughout the article, alongside alternative methods to approach the problem. By the end, you'll be equipped to solve similar problems with confidence.
Method 1: The Reciprocal Method
This is the most common and efficient method for dividing by a fraction. The core principle is to transform the division problem into a multiplication problem by using the reciprocal of the fraction. The reciprocal of a fraction is simply the fraction flipped upside down.
-
Step 1: Find the reciprocal of 3/4. The reciprocal of 3/4 is 4/3.
-
Step 2: Change the division problem to a multiplication problem. Instead of 1 ÷ (3/4), we now have 1 × (4/3).
-
Step 3: Perform the multiplication. Multiplying 1 by any fraction results in that fraction. Therefore, 1 × (4/3) = 4/3.
-
Step 4: Simplify the fraction (if necessary). In this case, the fraction 4/3 is already in its simplest form. It can also be expressed as a mixed number: 1 1/3.
Therefore, 1 divided by 3/4 is 4/3 or 1 1/3.
Method 2: Using Common Denominators
While the reciprocal method is generally preferred for its efficiency, understanding the concept through common denominators provides valuable insight into the underlying principles. This method is particularly helpful for those still developing a strong grasp of fraction manipulation.
-
Step 1: Express 1 as a fraction with a denominator of 4. The number 1 can be expressed as any fraction where the numerator and denominator are equal. In this case, we choose 4/4 because it shares a denominator with 3/4.
-
Step 2: Perform the division. Now the problem becomes (4/4) ÷ (3/4). When dividing fractions with the same denominator, the denominators cancel out, leaving us with 4 ÷ 3.
-
Step 3: Express the result as a fraction. The result of 4 ÷ 3 is 4/3.
-
Step 4: Simplify the fraction (if necessary). Again, 4/3 is already in its simplest form and can be represented as 1 1/3.
Method 3: Visual Representation
Visualizing the problem can make the concept more intuitive, particularly for beginners. Imagine a whole pizza (representing the number 1). If you want to divide this pizza into portions of 3/4 each, how many portions will you get?
Imagine cutting the pizza into four equal slices. Each slice is 1/4 of the pizza. Three of these slices make up 3/4 (one portion). Since you have four slices in total, you can make 4/3 portions of 3/4 each from one whole pizza. This reinforces the answer we obtained through the other methods.
The Mathematical Explanation: Why Does the Reciprocal Work?
The success of the reciprocal method stems from the definition of division. Dividing by a number is the same as multiplying by its multiplicative inverse (reciprocal). Let's explore this further.
Consider the general division problem a ÷ b. We can rewrite this as a × (1/b). The term 1/b is the multiplicative inverse of b, meaning that b × (1/b) = 1. This principle extends to fractions as well.
When we divide 1 by 3/4, we are effectively asking: "What number, when multiplied by 3/4, equals 1?". The answer is 4/3, because (3/4) × (4/3) = 1. This confirms the validity of the reciprocal method and the answer 4/3 (or 1 1/3).
Real-World Applications
Understanding division with fractions is crucial for many real-world applications:
- Cooking and Baking: Scaling recipes up or down often involves dividing fractional amounts.
- Sewing and Crafting: Calculating fabric yardage or material quantities often requires fractional arithmetic.
- Construction and Engineering: Dividing measurements and calculating material needs frequently involves fractions.
- Data Analysis: Working with datasets often involves calculating proportions and averages, requiring fraction manipulation.
Frequently Asked Questions (FAQ)
-
Q: Can I use a calculator to solve this problem? A: Yes, most calculators can handle fraction division. However, understanding the underlying principles is crucial for solving more complex problems and building a strong mathematical foundation.
-
Q: What if the number being divided is not 1? A: The reciprocal method still applies. For example, to solve 2 ÷ (3/4), you would calculate 2 × (4/3) = 8/3 or 2 2/3.
-
Q: Why is 4/3 the same as 1 1/3? A: The fraction 4/3 represents four thirds. Since three thirds equal one whole, 4/3 contains one whole and one-third remaining (1 + 1/3 = 1 1/3).
-
Q: What if I have a more complex fraction division problem? A: The same principles apply. For example, to solve (2/5) ÷ (3/7), you would calculate (2/5) × (7/3) = 14/15.
Conclusion: Mastering Fraction Division
Dividing by fractions might initially seem daunting, but by understanding the reciprocal method and the underlying mathematical principles, it becomes a manageable and even enjoyable process. This guide provides multiple approaches – the reciprocal method, the common denominator method, and a visual representation – to cater to diverse learning styles. Remember that practice is key to mastering this fundamental skill. By working through various examples, you'll build confidence and solidify your understanding of fraction division. The ability to comfortably handle fractions is essential for success in numerous academic and real-world contexts. Don't hesitate to revisit these methods and try some practice problems on your own. You'll be amazed how quickly you'll become proficient in solving fraction division problems.
Latest Posts
Latest Posts
-
Sport Brings People Together Speech
Sep 21, 2025
-
What Are The Describing Words
Sep 21, 2025
-
Doha Currency To Australian Dollar
Sep 21, 2025
-
Pictures Of Fruit And Vegetables
Sep 21, 2025
-
Difference Between Nucleus And Nucleolus
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 1 Divided By 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.