1 Divided By 1 3
candidatos
Sep 17, 2025 · 5 min read
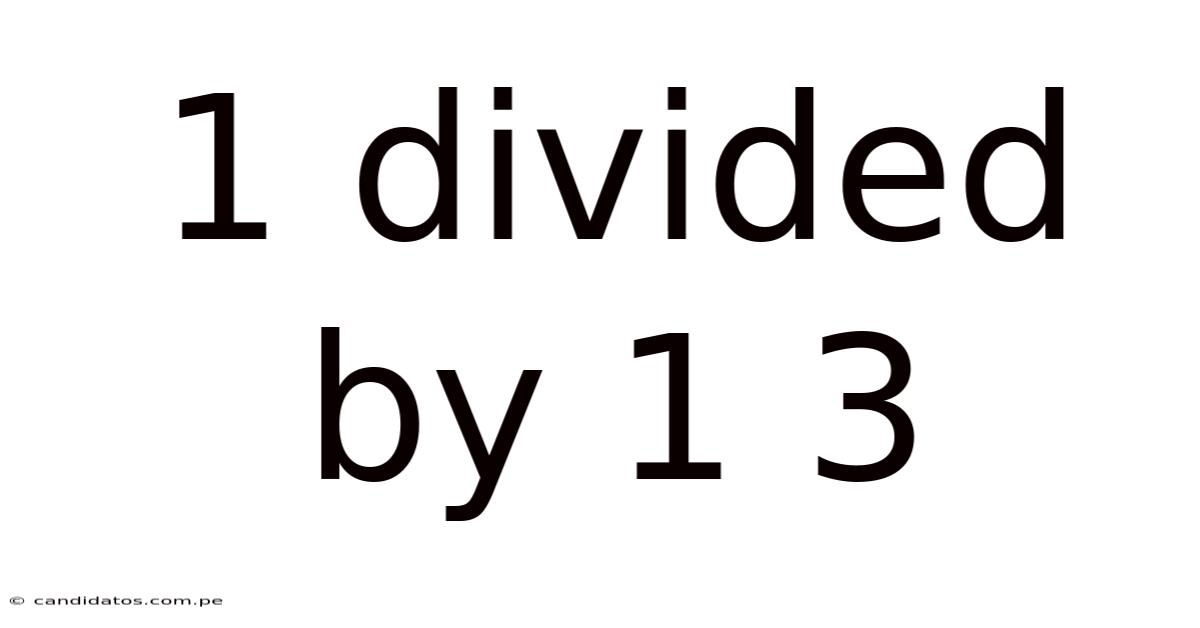
Table of Contents
Decoding 1 Divided by 1 1/3: A Deep Dive into Fractions and Division
This article explores the seemingly simple yet conceptually rich problem of dividing 1 by the mixed number 1 1/3. We'll break down the process step-by-step, exploring the underlying principles of fraction division, offering multiple solution methods, and addressing common misconceptions. Understanding this calculation provides a solid foundation for more complex fraction manipulations crucial in various fields, from baking and carpentry to advanced mathematics and engineering. This comprehensive guide aims to equip you with not just the answer but a deep understanding of the 'why' behind the calculation.
Understanding the Problem: 1 ÷ 1 1/3
At first glance, 1 ÷ 1 1/3 appears straightforward. However, the presence of a mixed number (a whole number and a fraction) introduces a layer of complexity. To solve this, we must first understand how to handle division with fractions. The core concept lies in converting the mixed number into an improper fraction, allowing for easier manipulation and calculation.
Converting Mixed Numbers to Improper Fractions
A mixed number, like 1 1/3, represents a whole number plus a fraction. To convert it into an improper fraction (where the numerator is larger than the denominator), we follow these steps:
- Multiply the whole number by the denominator: 1 x 3 = 3
- Add the numerator to the result: 3 + 1 = 4
- Keep the same denominator: 3
Therefore, 1 1/3 is equivalent to the improper fraction 4/3. Our problem now transforms into 1 ÷ 4/3.
Methods for Dividing Fractions
There are several ways to approach fraction division. Let's explore two common and effective methods:
Method 1: The "Keep, Change, Flip" Method
This intuitive method simplifies the division process. It involves three steps:
- Keep: Keep the first fraction (in our case, 1, which can be written as 1/1) as it is.
- Change: Change the division sign (÷) to a multiplication sign (x).
- Flip: Flip the second fraction (reciprocal). The reciprocal of 4/3 is 3/4.
Therefore, 1 ÷ 4/3 becomes 1/1 x 3/4.
Method 2: The "Common Denominator" Method
This method involves converting both fractions to have a common denominator before performing the division. While it might seem more complex initially, it reinforces the fundamental understanding of fractions.
- Find a common denominator: In this case, the common denominator for 1/1 and 4/3 is 3.
- Convert the fractions: 1/1 becomes 3/3.
- Perform the division: (3/3) ÷ (4/3) can be thought of as (3 ÷ 4) / (3 ÷ 3). This simplifies to 3/4.
Both methods yield the same result: 3/4.
Calculating the Result: 1 ÷ 1 1/3 = 3/4
Following either method, we arrive at the solution: 1 divided by 1 1/3 equals 3/4. This means that if you divide a whole unit into portions the size of 1 1/3, you get three-quarters of a portion.
Visualizing the Solution
Imagine a pizza cut into three slices. Each slice represents 1/3 of the pizza. 1 1/3 pizzas would be four of these slices. If you want to determine what portion of a whole pizza is represented by one slice, then each slice represents 3/4 of a whole pizza.
Expanding the Understanding: Real-World Applications
The ability to perform such calculations is essential in various real-world scenarios:
- Baking: Scaling down recipes often involves dividing ingredient amounts.
- Construction/Carpentry: Precise measurements and material calculations are paramount.
- Sewing/Crafting: Dividing fabric or yarn for projects requires accurate fraction division.
- Finance: Calculating portions of investments or expenses.
- Data Analysis: Working with proportions and ratios in statistical data.
Addressing Common Misconceptions
A frequent mistake is to incorrectly attempt direct division of the whole number and the fraction separately. Remember, the mixed number must be treated as a single entity (an improper fraction) before performing the division.
Another misconception involves incorrectly flipping both fractions during the "keep, change, flip" method. Only the second fraction is flipped; the first fraction remains unchanged.
Further Exploration: Complex Fraction Division
The principles discussed here can be extended to more complex problems involving multiple fractions and mixed numbers. Consistent practice and a solid understanding of fraction manipulation are key to mastering these concepts. The ability to convert between mixed numbers and improper fractions, and the efficient use of the "keep, change, flip" method or the "common denominator" method are fundamental.
Frequently Asked Questions (FAQ)
-
Q: Can I use a calculator to solve this problem?
- A: Yes, most scientific calculators can handle fraction division. However, understanding the underlying mathematical principles is crucial for problem-solving beyond simple calculations.
-
Q: What if the first number wasn't 1?
- A: The process remains the same. Convert any mixed numbers to improper fractions, then apply the "keep, change, flip" or "common denominator" method.
-
Q: Why is the reciprocal used in the "keep, change, flip" method?
- A: Dividing by a fraction is equivalent to multiplying by its reciprocal. This is a fundamental property of fraction division.
-
Q: Is there only one correct way to solve this?
- A: While there are different methods, they all lead to the same mathematically correct answer. Choose the method you find most intuitive and efficient.
Conclusion: Mastering Fraction Division
The seemingly simple problem of 1 divided by 1 1/3 reveals the richness and importance of understanding fractions and fraction division. By mastering the conversion between mixed numbers and improper fractions, and applying the appropriate division methods, you build a strong foundation for tackling more complex mathematical challenges. This knowledge is not limited to theoretical mathematics; it's a practical skill applicable to various aspects of everyday life and professional endeavors. Continue practicing these techniques, and you’ll find yourself confidently navigating the world of fractions with ease and precision. Remember, the journey to mastering fractions is a process of understanding the underlying concepts, and the more you practice, the more confident you will become.
Latest Posts
Latest Posts
-
Difference Between Monitor And Tv
Sep 17, 2025
-
Convert Cal To Kj Calculator
Sep 17, 2025
-
How Long Is 160 Minutes
Sep 17, 2025
-
When Is Hsc Exam 2024
Sep 17, 2025
-
Is The Haber Process Exothermic
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 1 Divided By 1 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.