1 50 As A Percent
candidatos
Sep 20, 2025 · 5 min read
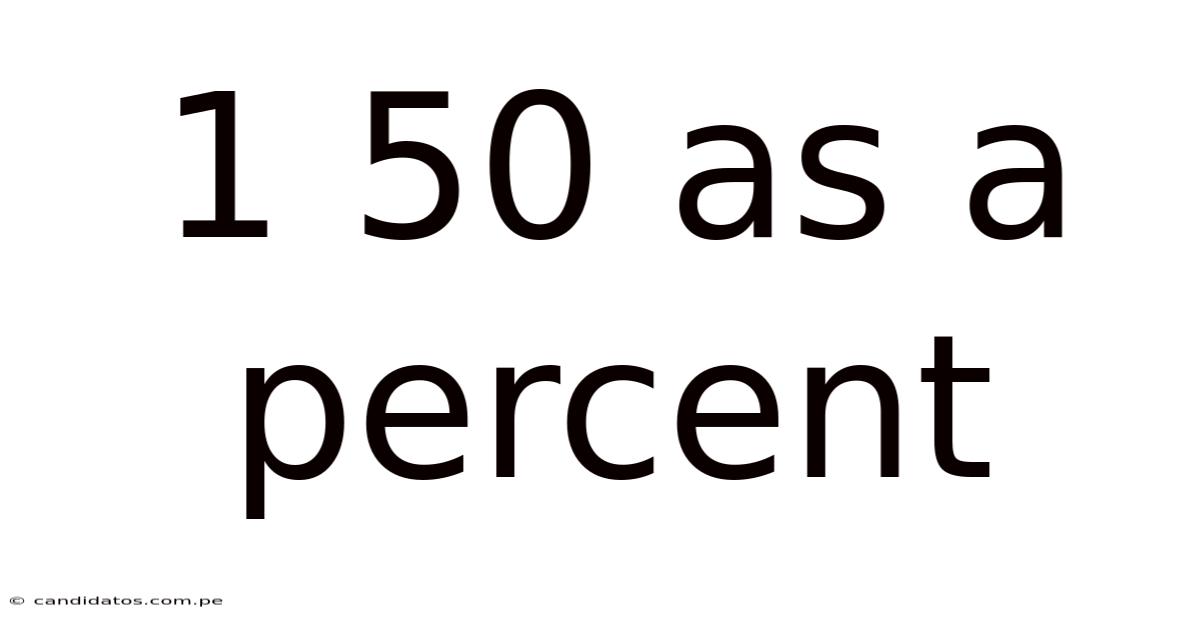
Table of Contents
1/50 as a Percent: Understanding Fractions, Decimals, and Percentages
Understanding how to convert fractions into percentages is a fundamental skill in mathematics with applications spanning numerous fields, from finance and statistics to everyday budgeting and cooking. This comprehensive guide will walk you through the process of converting the fraction 1/50 into a percentage, explaining the underlying concepts and offering practical examples to solidify your understanding. We'll also explore related concepts and answer frequently asked questions to ensure a thorough grasp of this essential mathematical transformation.
Understanding Fractions, Decimals, and Percentages
Before diving into the conversion, let's refresh our understanding of the three key concepts: fractions, decimals, and percentages.
-
Fractions: A fraction represents a part of a whole. It's expressed as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). For example, in the fraction 1/50, 1 is the numerator and 50 is the denominator. This means one part out of fifty equal parts.
-
Decimals: Decimals are another way to represent parts of a whole. They use a base-ten system, with digits to the right of the decimal point representing tenths, hundredths, thousandths, and so on. For instance, 0.2 represents two tenths, and 0.25 represents twenty-five hundredths.
-
Percentages: Percentages represent a fraction or decimal as a portion of 100. The symbol "%" signifies "per cent," meaning "out of one hundred." Therefore, 50% means 50 out of 100, or 50/100.
Converting 1/50 to a Decimal
The first step in converting 1/50 to a percentage is to convert it to a decimal. To do this, we simply divide the numerator (1) by the denominator (50):
1 ÷ 50 = 0.02
Therefore, the decimal equivalent of 1/50 is 0.02.
Converting the Decimal to a Percentage
Now that we have the decimal equivalent (0.02), converting it to a percentage is straightforward. We multiply the decimal by 100 and add the percentage symbol (%):
0.02 × 100 = 2
So, 0.02 as a percentage is 2%.
Therefore, 1/50 is equal to 2%.
A Step-by-Step Guide: Converting Any Fraction to a Percentage
The process demonstrated above can be applied to any fraction. Here's a generalized step-by-step guide:
-
Divide the numerator by the denominator: This will give you the decimal equivalent of the fraction.
-
Multiply the decimal by 100: This converts the decimal to a percentage.
-
Add the percentage symbol (%): This signifies that the number represents a percentage.
Practical Applications of Percentage Conversions
The ability to convert fractions to percentages is crucial in various real-world scenarios:
-
Finance: Calculating interest rates, discounts, profit margins, and tax rates all involve working with percentages.
-
Statistics: Percentages are essential for representing data and analyzing trends in surveys, polls, and other statistical studies.
-
Everyday Life: Calculating tips, sales discounts, and understanding proportions in recipes all require understanding percentages.
Understanding Percentage Increase and Decrease
While this article focuses on converting a simple fraction, understanding percentage change is equally important. Let's illustrate this with an example.
Suppose you had 50 apples, and you sold 1 apple. To express this as a percentage decrease, we follow these steps:
-
Calculate the change: You sold 1 apple out of 50, so the change is 1.
-
Divide the change by the original amount: 1 ÷ 50 = 0.02
-
Multiply by 100 to express as a percentage: 0.02 × 100 = 2%
Therefore, selling 1 apple out of 50 represents a 2% decrease.
Working with Larger and Smaller Fractions
The principles remain the same when working with larger or smaller fractions. For example:
-
Converting 25/50 to a percentage:
25 ÷ 50 = 0.5 0.5 × 100 = 50%
-
Converting 1/100 to a percentage:
1 ÷ 100 = 0.01 0.01 × 100 = 1%
-
Converting 1/200 to a percentage:
1 ÷ 200 = 0.005 0.005 × 100 = 0.5%
Understanding the Relationship Between Fractions, Decimals, and Percentages
It's important to understand the interconnectedness of these three representations of portions of a whole. They are simply different ways of expressing the same value. The ability to easily convert between them is a valuable mathematical skill.
Frequently Asked Questions (FAQ)
Q1: Why is understanding percentage conversions important?
A1: Percentage conversions are crucial for understanding and working with proportions, ratios, and data representation in numerous fields, from finance to science. They simplify comparisons and make numerical information more accessible.
Q2: What if I have a fraction with a larger numerator than denominator?
A2: If the numerator is larger than the denominator (an improper fraction), the resulting percentage will be greater than 100%. For example, 50/25 = 2, which is equivalent to 200%.
Q3: Can I use a calculator to convert fractions to percentages?
A3: Yes, most calculators can handle this calculation directly. Simply divide the numerator by the denominator and then multiply the result by 100.
Q4: Are there any shortcuts for converting common fractions to percentages?
A4: Yes, with practice, you'll become familiar with common fraction-to-percentage equivalents. For example, you'll quickly recognize that 1/4 is 25%, 1/2 is 50%, and 3/4 is 75%.
Q5: What are some real-world examples where this skill is used?
A5: Calculating discounts on sale items, understanding interest rates on loans, interpreting statistical data presented as percentages, and determining the percentage of a grade received on a test all require this skill.
Conclusion
Converting 1/50 to a percentage, resulting in 2%, is a simple yet foundational concept in mathematics. Understanding this conversion, along with the broader concepts of fractions, decimals, and percentages, is essential for anyone who works with numerical data or needs to understand proportions in everyday life. Mastering this skill will significantly improve your numerical literacy and problem-solving abilities across a wide range of applications. Practice regularly, and you'll soon find yourself confident and proficient in converting fractions, decimals, and percentages with ease. Remember to utilize the step-by-step process outlined above and refer back to this guide as needed to solidify your understanding. The more you practice, the more intuitive this process will become.
Latest Posts
Latest Posts
-
5 Letter Word Start Sa
Sep 20, 2025
-
Rectangle Moment Of Inertia Formula
Sep 20, 2025
-
Conversion Metric To Imperial Table
Sep 20, 2025
-
Convert Meters To Square Meters
Sep 20, 2025
-
As 3600 Pdf Free Download
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 1 50 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.