1 4 X 5 8
candidatos
Sep 23, 2025 · 6 min read
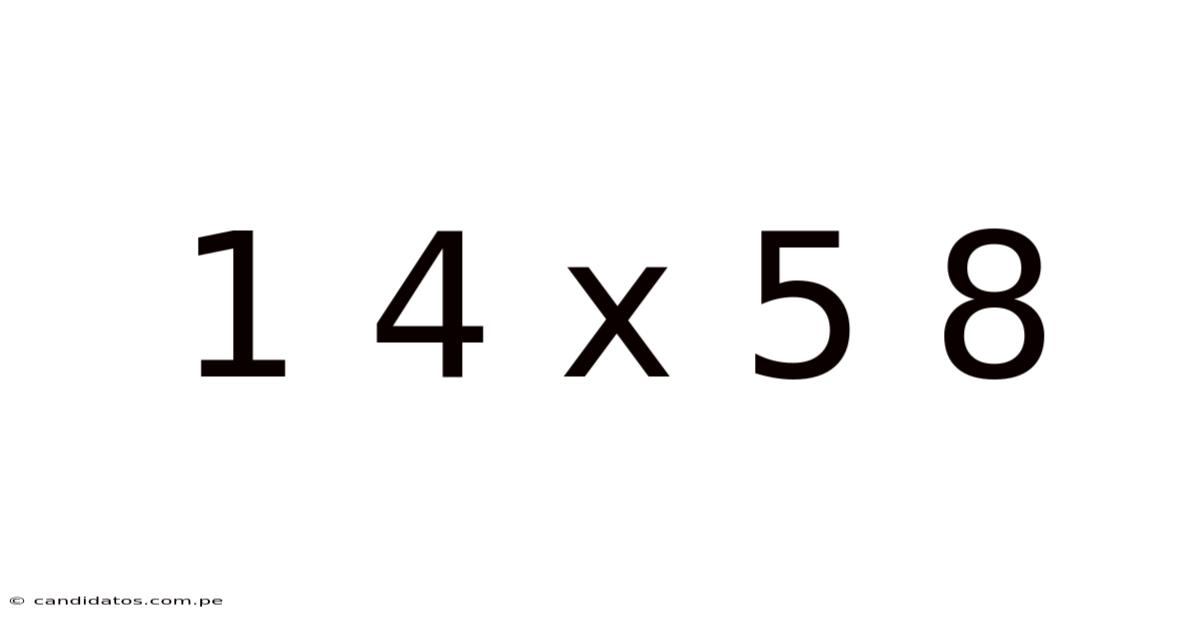
Table of Contents
Decoding 14 x 58: A Deep Dive into Multiplication and its Applications
This article explores the seemingly simple multiplication problem 14 x 58, delving far beyond the immediate answer to uncover the underlying mathematical principles and the vast range of applications this basic operation holds in various fields. We'll examine different methods of solving the problem, explore the historical context of multiplication, and highlight its relevance in everyday life, science, and advanced mathematics. Understanding 14 x 58 isn't just about getting the right number; it's about grasping the fundamental building blocks of numerical computation and their profound impact on our world.
Understanding the Fundamentals: What is Multiplication?
At its core, multiplication is a concise way of representing repeated addition. When we say 14 x 58, we're essentially saying "add 14 to itself 58 times." While this approach is conceptually straightforward, it's incredibly inefficient for larger numbers. This is why various methods and algorithms have been developed to streamline the multiplication process.
Methods for Solving 14 x 58
Several approaches can be employed to solve 14 x 58. Let's explore a few:
1. Standard Algorithm (Long Multiplication): This is the method most commonly taught in schools.
- Step 1: Multiply 14 by 8 (the units digit of 58): 14 x 8 = 112. Write down 2 and carry-over 11.
- Step 2: Multiply 14 by 5 (the tens digit of 58): 14 x 5 = 70. Add the carry-over 11: 70 + 11 = 81.
- Step 3: Combine the results: 812.
Therefore, 14 x 58 = 812.
2. Distributive Property: This method leverages the distributive property of multiplication over addition. We can break down 58 into 50 + 8:
- 14 x (50 + 8) = (14 x 50) + (14 x 8) = 700 + 112 = 812
This approach highlights the fundamental algebraic property that underpins multiplication.
3. Lattice Multiplication: This ancient method, used for centuries, offers a visual approach:
- Draw a grid with two rows (for 14) and two columns (for 58).
- Multiply each digit individually and write the result within the corresponding cell, separating tens and units.
- Add the diagonals to obtain the final result.
While more visually intensive, lattice multiplication offers a systematic way to handle larger numbers.
4. Using a Calculator: In the modern era, calculators provide a quick and efficient way to solve multiplication problems. While convenient, it's crucial to understand the underlying principles to appreciate the power and versatility of multiplication.
The Historical Context of Multiplication
Multiplication, like other fundamental arithmetic operations, has evolved over centuries. Early civilizations employed various techniques, often relying on visual aids and physical manipulatives. The development of place-value systems, like the Hindu-Arabic numeral system, significantly improved the efficiency of multiplication. The invention of the abacus and later, mechanical calculators, revolutionized mathematical computation, leading to the sophisticated digital tools we use today. The history of multiplication underscores the enduring human quest for efficient and effective methods to solve numerical problems.
Applications of Multiplication Across Disciplines
The simple act of multiplying 14 by 58 might seem inconsequential, but its implications extend far beyond a single calculation. Multiplication forms the bedrock of numerous fields:
1. Everyday Life: From calculating the total cost of groceries to determining the area of a room, multiplication is ingrained in our daily routines. Calculating distances traveled, figuring out the number of items needed for a project, or even splitting a bill among friends all involve multiplication.
2. Science and Engineering: Multiplication is essential in various scientific disciplines. Physics utilizes multiplication in calculating forces, velocities, and energies. Chemistry employs it in stoichiometry, determining the quantities of reactants and products in chemical reactions. Engineering relies heavily on multiplication in designing structures, calculating stresses and strains, and analyzing systems.
3. Finance and Economics: Multiplication plays a critical role in financial calculations. Calculating interest, determining profits and losses, and analyzing investment returns all rely on multiplication. Economic modeling also frequently utilizes multiplicative relationships to forecast trends and analyze market behavior.
4. Computer Science: Multiplication is fundamental to computer programming and algorithm design. It's used in matrix operations, image processing, and various other computational tasks. The speed and efficiency of multiplication algorithms have a direct impact on the performance of computer systems.
5. Advanced Mathematics: Multiplication extends beyond basic arithmetic. It's integral to algebra, calculus, linear algebra, and numerous other advanced mathematical fields. Understanding multiplication is crucial for grasping more complex mathematical concepts.
Expanding the Understanding: Exploring Related Concepts
Understanding 14 x 58 allows us to explore related mathematical concepts:
- Factors and Multiples: 14 and 58 are factors of 812, while 812 is a multiple of both 14 and 58. Exploring factors and multiples helps build a deeper understanding of number relationships.
- Prime Factorization: Breaking down numbers into their prime factors provides insights into their composition. The prime factorization of 812, for instance, reveals the fundamental building blocks of this number.
- Divisibility Rules: Knowing divisibility rules can help determine if a number is divisible by specific factors without performing long division. For example, divisibility rules for 2, 3, and other numbers are useful in simplifying calculations.
- Order of Operations (PEMDAS/BODMAS): Understanding the order of operations (Parentheses/Brackets, Exponents/Orders, Multiplication and Division, Addition and Subtraction) is crucial when dealing with complex expressions involving multiple operations.
Frequently Asked Questions (FAQs)
Q: What are some real-world examples where 14 x 58 might be used?
A: Imagine a farmer planting 14 rows of trees with 58 trees in each row. Multiplying 14 x 58 would tell them the total number of trees planted. Similarly, a contractor might need to calculate the total cost of 14 identical items priced at $58 each.
Q: Is there a faster way to multiply large numbers than long multiplication?
A: Yes, several advanced algorithms exist, such as the Karatsuba algorithm and the Fast Fourier Transform (FFT) algorithm, that significantly improve the speed of multiplication for extremely large numbers. These algorithms are primarily used in computer science and advanced computational tasks.
Q: Why is it important to understand multiplication beyond getting the answer?
A: Understanding the underlying principles of multiplication is crucial for developing strong mathematical reasoning skills. It's not just about memorizing facts but about grasping the conceptual foundations that underpin more advanced mathematical concepts.
Q: How can I improve my multiplication skills?
A: Consistent practice is key. Start with smaller numbers and gradually increase the difficulty. Use different methods, explore visual aids, and utilize online resources or educational apps to reinforce your understanding.
Conclusion: The Enduring Significance of 14 x 58
While 14 x 58 might seem like a simple arithmetic problem, its significance extends far beyond the answer 812. It represents a fundamental building block of mathematics, with applications spanning numerous fields. Understanding this seemingly simple calculation not only equips us with practical skills but also fosters critical thinking and a deeper appreciation for the interconnectedness of mathematical concepts. From everyday calculations to advanced scientific applications, the power of multiplication is undeniable, and the seemingly simple problem of 14 x 58 serves as a microcosm of its immense influence. Mastering multiplication is not merely about achieving the correct numerical result, it's about unlocking a world of mathematical possibilities.
Latest Posts
Latest Posts
-
Vegetables That Start With B
Sep 23, 2025
-
Different Between Sterilization And Disinfection
Sep 23, 2025
-
Life Cycle Of A Snail
Sep 23, 2025
-
Integral For Inverse Trig Functions
Sep 23, 2025
-
20 Percent Of 600 Thousand
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 1 4 X 5 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.