1 20th As A Percentage
candidatos
Sep 15, 2025 · 5 min read
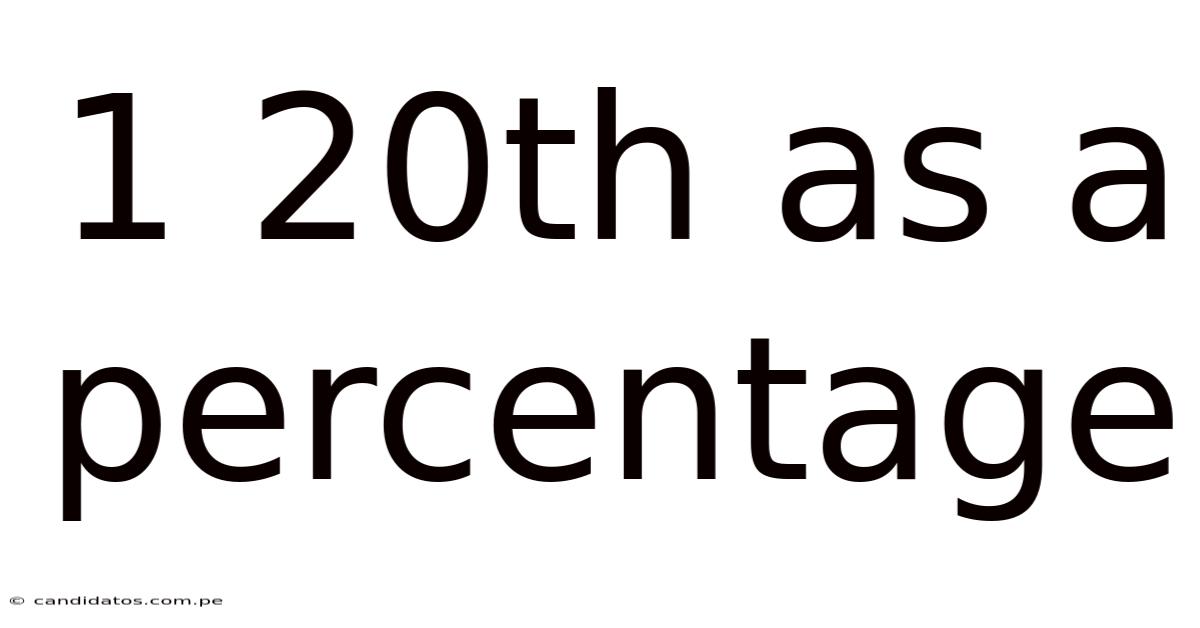
Table of Contents
Understanding 1/20th as a Percentage: A Comprehensive Guide
Understanding fractions and their percentage equivalents is a fundamental skill in mathematics with broad applications in daily life, from calculating discounts to comprehending financial reports. This article delves deep into converting the fraction 1/20th into a percentage, explaining the process step-by-step and exploring its practical implications. We’ll cover the underlying mathematical principles, provide practical examples, and address frequently asked questions to ensure a comprehensive understanding for learners of all levels.
Introduction: Fractions, Decimals, and Percentages
Before diving into the specific conversion of 1/20th, let's review the relationship between fractions, decimals, and percentages. These three represent different ways of expressing parts of a whole.
-
Fractions: Express a part of a whole as a ratio of two numbers (numerator/denominator). For example, 1/20 represents one part out of twenty equal parts.
-
Decimals: Express a part of a whole using base-ten notation, where the position of the digits represents powers of ten. For example, 0.5 represents one-half.
-
Percentages: Express a part of a whole as a fraction of 100. The symbol "%" represents "per hundred." For example, 50% represents fifty parts out of one hundred.
These three systems are interchangeable; we can convert between them using simple mathematical operations. This interchangeability is crucial for solving various problems in different contexts.
Converting 1/20th to a Percentage: A Step-by-Step Guide
Converting a fraction to a percentage involves two main steps:
Step 1: Convert the fraction to a decimal.
To convert 1/20 to a decimal, we simply divide the numerator (1) by the denominator (20):
1 ÷ 20 = 0.05
Step 2: Convert the decimal to a percentage.
To convert a decimal to a percentage, we multiply the decimal by 100 and add the "%" symbol:
0.05 x 100 = 5%
Therefore, 1/20 is equal to 5%.
Understanding the Mathematical Principles
The conversion process relies on the fundamental concept of proportionality. A percentage is essentially a fraction with a denominator of 100. When we convert 1/20 to a percentage, we are finding an equivalent fraction with a denominator of 100.
We can express this mathematically as follows:
1/20 = x/100
To solve for 'x' (the numerator of the equivalent fraction), we cross-multiply:
20x = 100
x = 100 ÷ 20
x = 5
Therefore, 1/20 is equivalent to 5/100, which is written as 5%.
Practical Applications of 1/20th (5%)
Understanding the equivalence of 1/20th and 5% has various practical applications in everyday life and various fields:
-
Calculating discounts: A 5% discount on a $100 item would mean a saving of $5 (5% of $100).
-
Determining tax rates: If a sales tax is 5%, you would pay $5 in tax for every $100 spent.
-
Analyzing financial statements: Understanding percentages is crucial for interpreting financial reports, such as profit margins or growth rates. A 5% increase in sales, for instance, indicates a significant improvement.
-
Understanding survey results: In surveys, 5% of respondents representing a particular demographic can provide valuable insights.
-
Medical dosage calculations: Although this requires more complex calculations than simple percentage conversion, understanding fractions and their percentage equivalents is fundamental to calculating medicine dosages accurately.
Further Exploration: Working with Larger and Smaller Fractions
While 1/20th is a relatively straightforward fraction to convert, the same principles apply to more complex fractions. To convert any fraction to a percentage, follow these steps:
-
Divide the numerator by the denominator to obtain a decimal.
-
Multiply the decimal by 100 to express it as a percentage.
For example, let's convert 3/5 to a percentage:
-
3 ÷ 5 = 0.6
-
0.6 x 100 = 60%
Therefore, 3/5 is equal to 60%. This same method can be applied to fractions with larger numerators and denominators.
Frequently Asked Questions (FAQ)
Q1: How do I convert a percentage back to a fraction?
To convert a percentage to a fraction, divide the percentage by 100 and simplify the resulting fraction. For example, to convert 25% to a fraction:
25% = 25/100 = 1/4
Q2: What if the decimal resulting from the division is recurring or non-terminating?
If the decimal is recurring (e.g., 1/3 = 0.333...), you may need to round the decimal to a certain number of decimal places before converting it to a percentage. The level of precision required depends on the context.
Q3: Are there any shortcuts for converting specific fractions to percentages?
Yes, there are. For example, knowing that 1/4 = 25%, 1/2 = 50%, and 3/4 = 75% can be useful shortcuts. These common fractions appear frequently in various applications. Memorizing these can significantly speed up your calculations.
Q4: What is the difference between a percentage and a percentage point?
This is a crucial distinction. A percentage represents a proportion of a whole, while a percentage point refers to the arithmetic difference between two percentages. For example, if a value increases from 20% to 25%, it has increased by 5 percentage points, not 5%.
Conclusion: Mastering Percentage Conversions
Understanding how to convert fractions like 1/20th into percentages is a valuable skill that transcends the boundaries of formal education. The ability to easily manipulate fractions, decimals, and percentages empowers you to analyze data, solve problems, and make informed decisions in numerous real-world situations. By understanding the underlying mathematical principles and practicing the conversion process, you can confidently tackle various percentage-related challenges in your academic pursuits, professional life, and everyday activities. Remember that the core concept revolves around proportionality – finding an equivalent fraction with a denominator of 100. Master this, and you’ll master percentages.
Latest Posts
Latest Posts
-
5 2 On Number Line
Sep 15, 2025
-
What Does The Circle Represent
Sep 15, 2025
-
Area Of A Half Cylinder
Sep 15, 2025
-
15 18 As A Percent
Sep 15, 2025
-
Is An Act A Law
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 1 20th As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.