1 100 As A Decimal
candidatos
Sep 23, 2025 · 6 min read
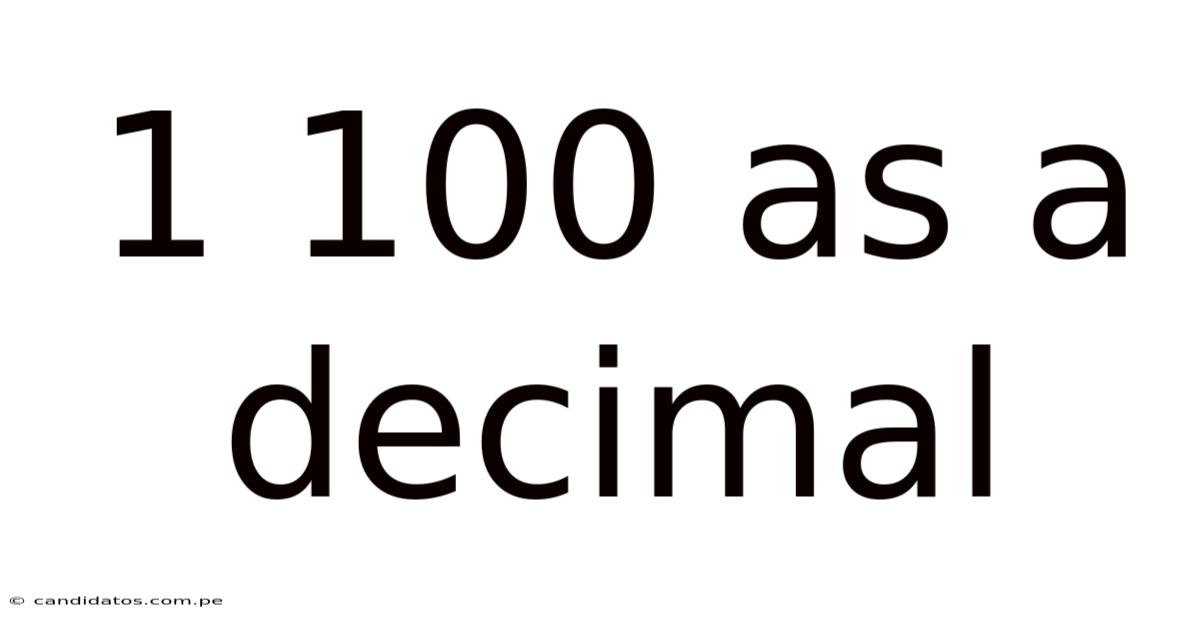
Table of Contents
Understanding 1/100 as a Decimal: A Comprehensive Guide
Many everyday situations require understanding fractions and their decimal equivalents. Converting fractions to decimals is a fundamental skill in mathematics, with applications ranging from simple calculations to complex scientific analyses. This article provides a comprehensive explanation of how to understand and represent 1/100 as a decimal, including the underlying mathematical principles and practical applications. We'll explore different methods for conversion and address frequently asked questions. By the end, you'll have a solid grasp of this seemingly simple yet crucial concept.
Understanding Fractions and Decimals
Before delving into the specifics of 1/100, let's briefly review the fundamental concepts of fractions and decimals. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts you have, while the denominator indicates how many equal parts the whole is divided into.
A decimal, on the other hand, represents a fraction where the denominator is a power of 10 (e.g., 10, 100, 1000, etc.). The decimal point separates the whole number part from the fractional part. The digits to the right of the decimal point represent the fractional part, with each place value representing a decreasing power of 10. For example, in 0.123, the 1 represents 1/10, the 2 represents 2/100, and the 3 represents 3/1000.
Converting 1/100 to a Decimal: The Direct Method
The simplest method to convert 1/100 to a decimal involves recognizing the denominator as a power of 10. Since 100 is 10², we can directly rewrite the fraction as a decimal. Remember that the denominator dictates the number of decimal places. Because the denominator is 100 (two zeros), the decimal will have two decimal places.
Therefore, 1/100 can be written as 0.01. The '1' is in the hundredths place, representing one-hundredth.
Converting 1/100 to a Decimal: Long Division Method
While the direct method is efficient for fractions with denominators that are powers of 10, the long division method offers a more general approach that works for any fraction. This method involves dividing the numerator (1) by the denominator (100).
1 ÷ 100 = 0.01
This confirms our earlier result. The long division process involves adding a decimal point and zeros to the dividend (1) to continue the division until the remainder is zero or the desired precision is reached.
Understanding Place Value in Decimals
Understanding place value is crucial for accurately interpreting and manipulating decimals. In the decimal 0.01:
- The digit before the decimal point represents the whole number (in this case, 0).
- The first digit after the decimal point represents the tenths place (0 in this case).
- The second digit after the decimal point represents the hundredths place (1 in this case).
- The third digit after the decimal point (if present) represents the thousandths place, and so on.
Practical Applications of 1/100 (0.01)
The decimal 0.01, or 1/100, has numerous practical applications across various fields:
-
Percentages: 0.01 is equivalent to 1%. This is because percentages represent parts per hundred. Therefore, 1% = 1/100 = 0.01. This is widely used in finance, statistics, and everyday life (e.g., calculating discounts, sales tax, interest rates).
-
Metric System: The metric system uses powers of 10 for its units. For instance, a centimeter is 1/100 of a meter (1 cm = 0.01 m). This consistency simplifies conversions between units.
-
Finance: 0.01 plays a significant role in financial calculations involving interest rates, currency exchange rates, and investment returns.
-
Science and Engineering: Many scientific and engineering calculations involve fractions and decimals, with 0.01 often representing a small but significant measurement or variation.
-
Probability: In probability, 0.01 represents a 1% probability of an event occurring.
Further Exploration: Converting Other Fractions to Decimals
The principles discussed above can be applied to convert other fractions to decimals. The key is to understand the relationship between the numerator and the denominator and how the denominator's value influences the placement of digits after the decimal point.
Here are a few examples:
- 1/10 = 0.1: The denominator is 10 (one zero), so there is one digit after the decimal point.
- 1/1000 = 0.001: The denominator is 1000 (three zeros), so there are three digits after the decimal point.
- 3/4 = 0.75: This requires long division (3 ÷ 4 = 0.75) or converting to an equivalent fraction with a denominator of 100 (75/100 = 0.75).
The method of conversion depends on the fraction's denominator. For denominators that are powers of 10, direct conversion is easiest. Otherwise, long division or conversion to an equivalent fraction with a power of 10 denominator is necessary.
Advanced Concepts: Repeating Decimals
Not all fractions convert to terminating decimals (decimals that end). Some fractions result in repeating decimals, where a sequence of digits repeats indefinitely. For example, 1/3 = 0.333... The '3' repeats infinitely. These repeating decimals can be expressed using a bar notation to indicate the repeating sequence (e.g., 0.3̅).
However, 1/100 is a simple fraction that conveniently converts to a terminating decimal (0.01), making it easier to work with in various calculations.
Frequently Asked Questions (FAQ)
Q: What is the difference between 1/100 and 100%?
A: They are equivalent. 1/100 represents one part out of a hundred, and 100% represents the whole, or all parts. They both equal 1. However, 1/100 is a fraction and 100% is a percentage.
Q: How can I convert a fraction with a denominator that is not a power of 10 to a decimal?
A: Use long division. Divide the numerator by the denominator. Add a decimal point and zeros to the numerator as needed to continue the division until you get a remainder of 0 or reach a desired level of accuracy.
Q: What are some real-world examples where 1/100 (0.01) is used?
A: Calculating 1% discounts, measuring centimeters in relation to meters, expressing probabilities, and representing small changes in scientific measurements.
Q: Is 0.01 a rational number?
A: Yes, 0.01 is a rational number because it can be expressed as the fraction 1/100, where both the numerator (1) and the denominator (100) are integers.
Conclusion
Understanding the representation of 1/100 as the decimal 0.01 is a fundamental skill in mathematics with wide-ranging applications. Mastering this conversion not only enhances your mathematical proficiency but also provides a solid foundation for more advanced concepts in various fields. Remember the direct method for easy conversion when the denominator is a power of 10, and long division for more general fraction-to-decimal conversions. Understanding place value is crucial for accurate interpretation and manipulation of decimals. By grasping these principles, you'll confidently navigate numerical tasks and solve problems involving fractions and decimals effectively. This knowledge will prove invaluable throughout your educational journey and in your future endeavors.
Latest Posts
Latest Posts
-
87 100 As A Percentage
Sep 23, 2025
-
Chemical Formula Of Silver Sulphate
Sep 23, 2025
-
Words That Have 3 Syllables
Sep 23, 2025
-
Body Tube In Microscope Function
Sep 23, 2025
-
Describing Words Beginning With J
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 1 100 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.