1 1 X 1 2
candidatos
Sep 23, 2025 · 6 min read
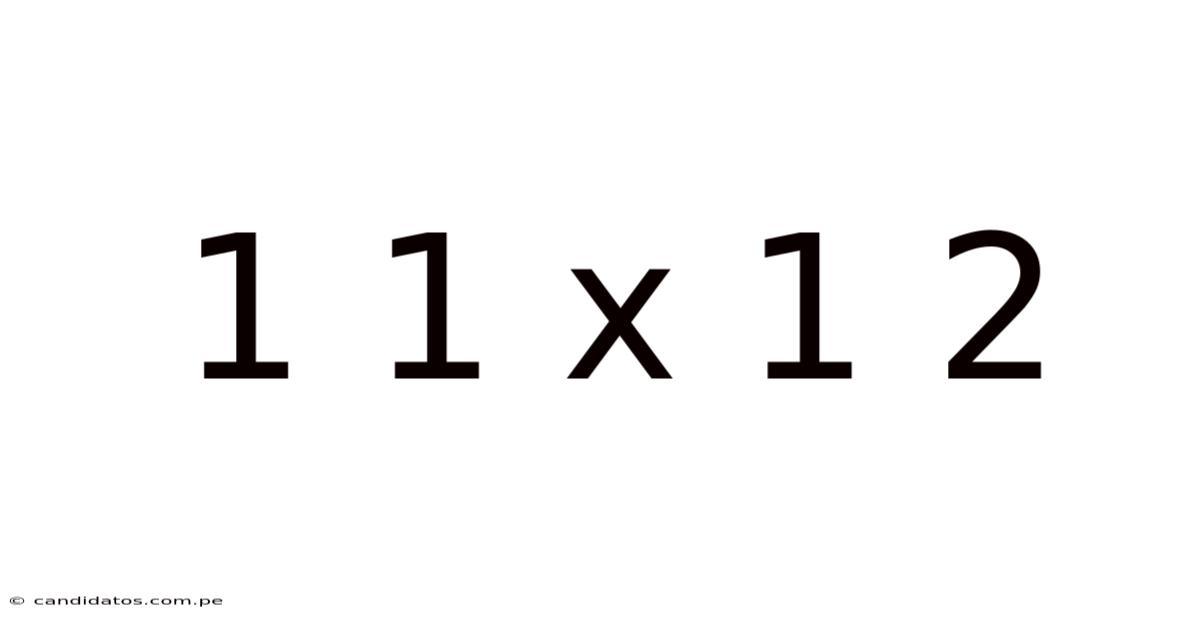
Table of Contents
Decoding 11 x 12: A Deep Dive into Multiplication and Beyond
This article explores the seemingly simple multiplication problem, 11 x 12, going beyond the immediate answer to delve into the underlying mathematical concepts, different calculation methods, and the broader applications of multiplication in various fields. We'll uncover the beauty of mathematics hidden within this seemingly basic equation, making it accessible and engaging for learners of all levels. Understanding 11 x 12 is not just about getting the answer; it's about building a strong foundation in numerical reasoning and problem-solving.
Introduction: More Than Just an Answer
At first glance, 11 x 12 might seem like a trivial arithmetic problem. The answer, 132, is readily obtainable with a calculator or through standard multiplication techniques. However, this seemingly simple equation offers a rich opportunity to explore fundamental mathematical concepts and develop essential skills applicable far beyond basic arithmetic. This article aims to unpack the layers of understanding embedded within this single calculation, illuminating the path towards a deeper appreciation of mathematics. We will explore various methods of solving this problem, highlighting the strengths and weaknesses of each approach and demonstrating the versatility of mathematical thinking.
Method 1: Standard Multiplication Algorithm
The most common method for solving 11 x 12 involves the standard multiplication algorithm taught in elementary schools. This method involves multiplying each digit of the first number by each digit of the second number, carrying over values when necessary, and then adding the partial products.
- Step 1: Multiply 11 by 2 (the units digit of 12): 11 x 2 = 22. Write down 2 and carry-over 2.
- Step 2: Multiply 11 by 1 (the tens digit of 12): 11 x 1 = 11. Add the carry-over 2: 11 + 2 = 13.
- Step 3: Combine the results: 132.
This method is straightforward and reliable, providing a systematic approach to solving multiplication problems. However, it relies on memorization of multiplication tables and can become cumbersome with larger numbers.
Method 2: Distributive Property
The distributive property of multiplication over addition is a fundamental concept in algebra. It states that a(b + c) = ab + ac. We can apply this to solve 11 x 12 as follows:
- Rewrite 11 as (10 + 1) and 12 as (10 + 2).
- Applying the distributive property: (10 + 1)(10 + 2) = 10(10 + 2) + 1(10 + 2)
- Expanding the equation: 100 + 20 + 10 + 2 = 132
This method demonstrates a deeper understanding of mathematical principles and helps lay the groundwork for more advanced algebraic manipulations.
Method 3: Lattice Multiplication
Lattice multiplication, an ancient method still relevant today, offers a visual and methodical approach to multiplication. It's particularly useful for larger numbers.
- Step 1: Create a grid (lattice) with two rows and two columns.
- Step 2: Write the digits of 11 along the top and the digits of 12 along the right side.
- Step 3: Multiply each digit pair and write the result in the corresponding cell, separating the tens and units digits with a diagonal line.
- Step 4: Sum the diagonals, carrying over values when necessary. The final answer is obtained by reading the numbers along the bottom and left sides.
This method helps visualize the multiplication process and can be adapted to solve problems with larger numbers more efficiently than the standard algorithm.
Method 4: Mental Math Techniques
For smaller multiplication problems like 11 x 12, mental math techniques can be highly efficient. One such technique involves recognizing patterns. Notice that multiplying by 11 often involves a simple pattern:
- 11 x 12 can be thought of as 11 x (10 + 2) = 110 + 22 = 132.
- Alternatively, consider 11 x 12 as 120 – 12 = 132
Another approach relies on breaking down the numbers into simpler components:
- 11 x 12 can be seen as (10 + 1) x (10 + 2), leading to the expanded form discussed in the distributive property method.
Mastering mental math techniques significantly improves calculation speed and reduces reliance on external tools.
The Significance of Understanding Different Methods
The importance of learning multiple methods for solving 11 x 12 extends beyond simply obtaining the correct answer. Exploring different approaches:
- Develops mathematical fluency: Understanding various methods enhances your overall mathematical understanding and problem-solving skills.
- Strengthens conceptual understanding: Methods like the distributive property and lattice multiplication illustrate fundamental mathematical concepts, providing a deeper insight into the principles underlying the operation.
- Enhances adaptability: Knowing different techniques enables you to choose the most efficient method depending on the problem's complexity and the available resources.
- Promotes critical thinking: Analyzing different approaches fosters critical thinking skills and encourages the exploration of alternative solutions.
- Improves problem-solving skills: Solving the same problem through different methods enhances your overall problem-solving capabilities, making you more resourceful and adaptable to diverse mathematical challenges.
Applications of Multiplication: Beyond the Classroom
Multiplication, as exemplified by 11 x 12, is not confined to the realm of theoretical mathematics. It's a fundamental operation with widespread practical applications across numerous fields:
- Engineering and Physics: Calculating forces, distances, areas, volumes, and other physical quantities.
- Finance and Business: Calculating profits, losses, interest, taxes, and other financial metrics.
- Computer Science: Performing arithmetic operations in algorithms and computer programs.
- Everyday Life: Calculating quantities, costs, measurements, and other aspects of daily living. From figuring out the total cost of groceries to determining the amount of paint needed to cover a wall.
Frequently Asked Questions (FAQs)
Q: What is the easiest way to calculate 11 x 12?
A: The easiest method depends on your individual preferences and mathematical background. For many, the standard multiplication algorithm is the most intuitive. However, mental math techniques can be quicker for smaller numbers.
Q: Why are there different methods for multiplication?
A: Different methods exist to cater to various learning styles, mathematical backgrounds, and problem complexities. Some methods highlight specific mathematical concepts, while others prioritize efficiency or visualization.
Q: Is lattice multiplication useful for larger numbers?
A: Yes, lattice multiplication is particularly helpful for larger numbers, as it provides a structured and less error-prone approach compared to the standard algorithm.
Q: Can I use a calculator to solve 11 x 12?
A: While a calculator provides a quick solution, understanding the underlying mathematical principles and different solution methods is crucial for developing strong mathematical skills and problem-solving abilities.
Conclusion: The Power of Understanding
Solving 11 x 12 is more than just getting the answer 132. It's about embracing the process of exploration, understanding the underlying mathematical principles, and appreciating the versatility of different calculation methods. Mastering multiplication isn't just about memorizing facts; it's about developing a deeper understanding of numbers and their relationships. The seemingly simple equation 11 x 12 serves as a powerful microcosm of mathematical thinking, highlighting the beauty and power of numbers and their applications in various aspects of life. By exploring diverse approaches and understanding the underlying concepts, we develop not just computational skills, but also critical thinking and problem-solving abilities that extend far beyond the classroom.
Latest Posts
Latest Posts
-
4 7 As A Percentage
Sep 23, 2025
-
Dividing Decimals By Decimals Worksheet
Sep 23, 2025
-
Is Domain X Or Y
Sep 23, 2025
-
First Flush In Rainwater Harvesting
Sep 23, 2025
-
Is Ammonium Acidic Or Basic
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 1 1 X 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.