1 1/7 As A Decimal
candidatos
Sep 18, 2025 · 5 min read
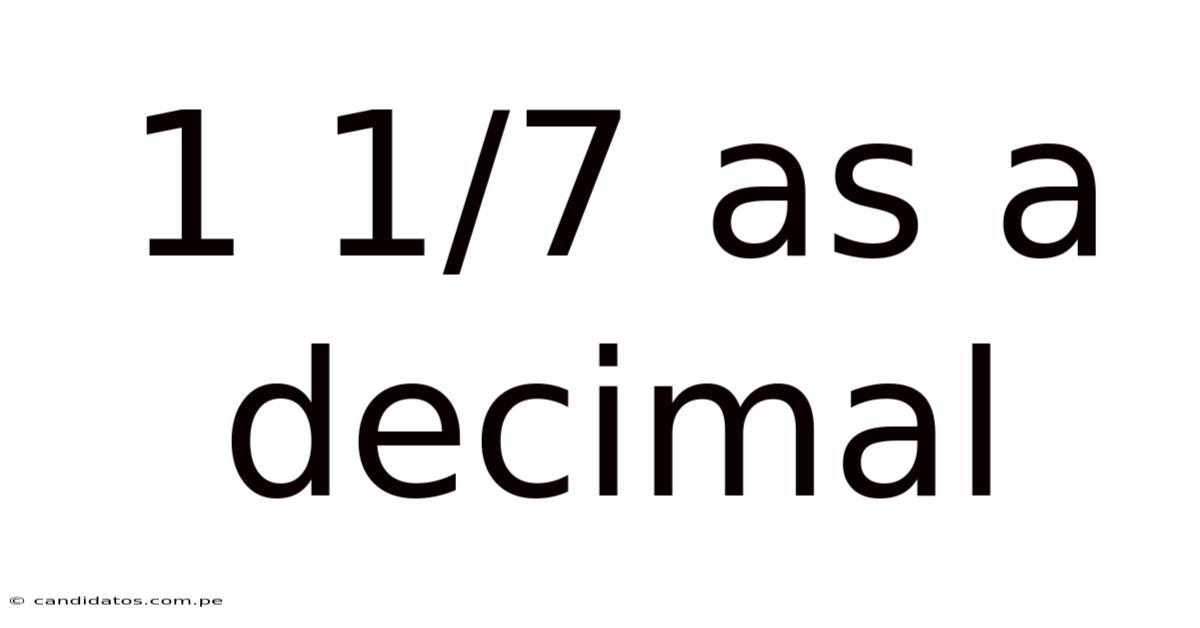
Table of Contents
Decoding 1 1/7 as a Decimal: A Comprehensive Guide
Understanding how to convert fractions to decimals is a fundamental skill in mathematics, applicable across various fields from everyday calculations to advanced scientific computations. This comprehensive guide delves into the process of converting the mixed fraction 1 1/7 into its decimal equivalent, providing a step-by-step explanation, exploring the underlying mathematical principles, addressing common questions, and offering valuable insights for further learning. This guide aims to clarify the process, making it accessible to everyone, regardless of their prior mathematical experience. We'll also explore the practical applications of understanding decimal representations of fractions.
Understanding Mixed Fractions and Decimals
Before we embark on the conversion, let's briefly review the concepts of mixed fractions and decimals. A mixed fraction combines a whole number and a proper fraction (a fraction where the numerator is smaller than the denominator). In our case, 1 1/7 represents one whole unit plus one-seventh of another unit. A decimal, on the other hand, expresses a number using a base-ten system, where the digits to the right of the decimal point represent tenths, hundredths, thousandths, and so on. Converting a fraction to a decimal essentially means expressing the fractional part as a decimal representation.
Step-by-Step Conversion of 1 1/7 to Decimal
The conversion of 1 1/7 to a decimal involves two main steps:
-
Convert the mixed fraction to an improper fraction: To do this, we multiply the whole number (1) by the denominator (7) and add the numerator (1). This result becomes the new numerator, while the denominator remains the same.
1 1/7 = (1 * 7 + 1) / 7 = 8/7
-
Divide the numerator by the denominator: Now, we perform the division: 8 divided by 7.
8 ÷ 7 = 1.142857142857...
Therefore, 1 1/7 as a decimal is approximately 1.142857. Notice the repeating decimal pattern: 142857.
Understanding the Repeating Decimal Pattern
The decimal representation of 1 1/7 exhibits a repeating decimal pattern, also known as a recurring decimal. This means that a sequence of digits repeats infinitely. In this case, the sequence "142857" repeats endlessly. This is a characteristic of many fractions where the denominator, when simplified, contains prime factors other than 2 and 5. This is because decimal representation is based on powers of 10 (2 x 5), and if the denominator contains any other prime factor, the division will result in a repeating decimal.
Mathematical Explanation of Repeating Decimals
The repeating decimal arises from the fact that when you perform long division of 8 by 7, the remainder never becomes zero. The division process continues indefinitely, producing the repeating sequence. This is a fundamental property of rational numbers (numbers that can be expressed as a fraction of two integers). Irrational numbers, like π (pi), have non-repeating, non-terminating decimal representations.
Rounding the Decimal
Since the decimal representation of 1 1/7 is non-terminating, we often need to round it to a specific number of decimal places for practical applications. The level of precision required depends on the context. For example:
- Rounded to two decimal places: 1.14
- Rounded to three decimal places: 1.143
- Rounded to four decimal places: 1.1429
Rounding involves examining the digit immediately following the desired decimal place. If this digit is 5 or greater, we round up; otherwise, we round down.
Practical Applications of Decimal Conversion
Understanding how to convert fractions to decimals is crucial in various situations:
-
Everyday Calculations: Dividing a pizza amongst friends, calculating discounts, or measuring ingredients for a recipe often involves fractional quantities, which are easier to work with in decimal form.
-
Financial Calculations: Interest rates, stock prices, and currency conversions frequently involve decimals. Understanding fraction-to-decimal conversion is essential for accurate financial calculations.
-
Science and Engineering: Scientific measurements and engineering designs require precise calculations, often involving fractions that need to be expressed in decimal form for use in formulas and equations.
-
Computer Programming: Many programming languages use floating-point numbers (decimal representations) for mathematical operations. Converting fractions to decimals is necessary for accurate programming involving calculations.
Frequently Asked Questions (FAQ)
Q: Why does 1/7 produce a repeating decimal?
A: The denominator 7 is a prime number other than 2 or 5. When a fraction's denominator (after simplification) contains prime factors other than 2 and 5, its decimal representation will be a repeating decimal. This is because the decimal system is based on powers of 10 (2 x 5), and division by other prime numbers leads to recurring remainders during the long division process.
Q: How can I check my decimal conversion for accuracy?
A: You can use a calculator to verify your calculations. However, be mindful that calculators may round the decimal representation, and very long repeating decimals might be truncated. The long division method is the most reliable way to determine the repeating pattern.
Q: Is there a quicker way to convert 1 1/7 to a decimal besides long division?
A: While long division is the fundamental method, using a calculator is the quickest way to obtain a decimal approximation. However, it's important to understand the underlying process to fully grasp the concept of repeating decimals and their mathematical basis.
Q: What if I need a very precise decimal representation of 1 1/7?
A: For very high precision, you would need to represent the decimal using a specific notation indicating the repeating sequence (e.g., using a bar over the repeating digits: 1.142857̅). This prevents rounding errors and retains the exact value.
Conclusion
Converting fractions to decimals, especially those with repeating decimal patterns like 1 1/7, is a crucial skill with broad applications. By understanding the mathematical principles behind the conversion and the nature of repeating decimals, you can confidently perform these calculations, ensuring accuracy and precision in various contexts. Remember, mastering this fundamental skill enhances your problem-solving abilities and empowers you to confidently tackle more complex mathematical challenges. The seemingly simple act of converting 1 1/7 to its decimal equivalent opens a door to a deeper understanding of number systems and their practical implications.
Latest Posts
Latest Posts
-
Convert 360 Fahrenheit To Celsius
Sep 18, 2025
-
Daily English Practice Book 3
Sep 18, 2025
-
A Cube In A Cube
Sep 18, 2025
-
Five Letter Words With Qu
Sep 18, 2025
-
Elements Compounds And Mixtures Worksheet
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 1 1/7 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.